最大限度降低单运算放大器滤波器的元件变化灵敏度

通过更深入地研究Sallen-Key滤波器的元件灵敏度，我们在数学分析中发现了一个“最佳点”，它允许设计简单的单运算放大器滤波器，其性能可与更复杂的滤波器相媲美。这种方法在扩展Sallen-Key滤波器的实用性方面很有用。

多年来，已经设计了数十种滤波器拓扑结构，每种拓扑都有自己的优势。然而，工程师通常依赖于这些拓扑中的一个小而流行的子组，这些子组可以使用“食谱”设计方法。他们为不太复杂的低阶设计选择更简单的单运放滤波器。但是，当相关的食谱方法无法开发行为良好的复杂滤波器时，工程师通常会转向更复杂的拓扑。但是，如果深入分析常见的单运算放大器拓扑（Sallen-Key滤波器），则可以得出一些有趣的结果。

典型的滤波器设计过程有三个主要阶段。首先，根据系统要求确定要通过的频率范围、允许的通带纹波等。接下来，您确定满足要求的传递函数（数学滤波器描述），通常通过选择标准类型之一：巴特沃斯、切比雪夫、贝塞尔、椭圆等。该过程中的这一步超出了本文的范围，但可以从末尾列出的参考文献中获得详细信息。

最后一步是设计和实现提供所需传递函数的电路。设计器通常遵循类似于以下内容的策略，该策略在应用于说明书拓扑时非常简单：

将传递函数分解为二阶部分。

选择允许独立合成每个二阶函数的电路拓扑。

将每个级设计为独立的二阶滤波器。

串联连接的二阶滤波器。

此时可能会出现说明书方法的共同限制。单运算放大器滤波器通常对其无源元件值的变化表现出很高的敏感性，而具有高Q值的滤波器（即大多数高阶滤波器）特别敏感。对于完美的无源元件来说，这种灵敏度不是问题，但实际元件仅在有限数量的标准值中可用。说明书计算可能需要 10.095k 电阻，但实际可用的最接近值可能是 10.0k。

实际组件值也因单元而异，并响应温度和其他环境因素的变化。滤波器对这些分量变化的敏感性可能导致其明显偏离其所需的频率响应。在许多情况下，设计人员会转向更复杂的滤波器拓扑。

萨伦基拓扑

Sallen-Key滤波器（基准电压源1）是最常见的单运算放大器滤波器之一。其低通版本（图1）具有以下设计公式：

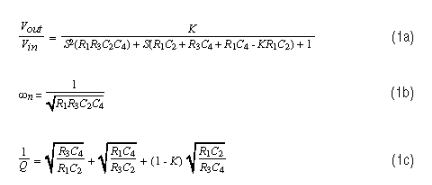
Q是“品质因数”（在固有频率附近发生的峰值的量度），K = 1 + RB/R一个是直流增益。

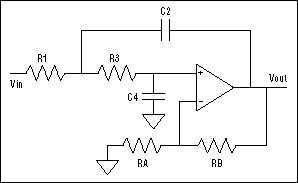
图1.

过滤器对组件变化的敏感性

固有频率和Q灵敏度有助于评估传递函数稳定性。对于Sallen-Key滤波器（在第2页的参考文献159中给出），这些灵敏度如下：

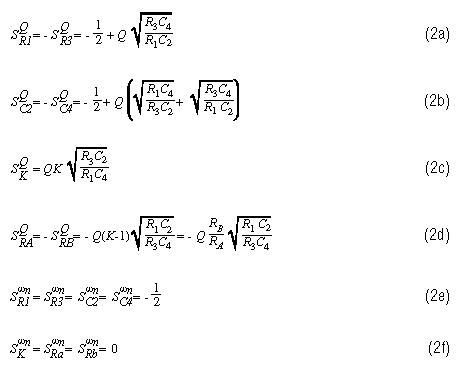
灵敏度用“S”表示。它的上标是正在评估其灵敏度的电路特性，其下标是正在评估其对该特性的影响的电路元件。因此，第一个灵敏度方程（2a）显示了Q对R变化的灵敏度1或 R3.

S是提高元件变化以计算电路特性中相应变化的功率。例如，您可能已经注意到，所有固有频率灵敏度的功率为 -1/2 或 0。当 S = -1/2 且分量变化系数为“A”时，固有频率变化 A-0.5（即1/√A）。因此，新的固有频率将是原始频率除以√A。当 S = 0 时，频率不会改变，因为 A0= 1。

参考文献2更详细地介绍了灵敏度，它包括上面列出的许多灵敏度方程的推导。参考文献3和4也对这一重要主题进行了很好的处理。这些方程非常复杂，通常很难为所需的固有频率和Q选择六个无源分量，同时实现低Q灵敏度，除非您玩弄方程并注意到当增益（K）设置为1时发生的一些有趣的事情。

K = 1 简化了萨伦键滤波器

我们可以通过选择K = 1作为直流增益值来大大简化Sallen-Key滤波器方程。在这种情况下，Q的方程（公式1c）简化为

我们还发现，当K = 1时，Q对RA和RB的灵敏度为零（等式2d）。这并不奇怪。设置K = 1时，运算放大器的输出直接连接到反相输入，从而将运算放大器配置为电压跟随器，从而消除了RA和RB。

将Q的简化方程（公式3）代入灵敏度方程2a和2c可简化这些方程：

通过将电阻值设置为相等，可以进一步简化Q对电阻的灵敏度。当R1和R3完全相等时，灵敏度为零。但实际电阻的值永远不会真正相等。当它们偏离其标称值时，灵敏度变为非零，但仍然非常小。例如，容差为 5% 的电阻会导致最坏情况的灵敏度

因此，5%的电阻变化会产生0.12%的Q变化，与其他灵敏度相比可以忽略不计。即使电阻值不相等，该灵敏度也在-1/2和+1/2之间。仔细观察Q方程，可以发现设置R1 = R3的其他原因：

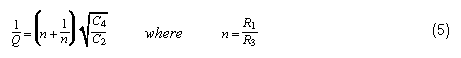
当 n = 1 时（即当 R3= R1），数量 （n+1/n） 的最小值为 2。因此，当Q = 1/2且电阻彼此相等时，滤波电容的值将相等。对于所有高于 1/2 的 Q（迄今为止最常见的情况），C2必须大于 C4.如果电阻不相等，则C的比值2到 C4必须做得更大。因此，为了最小化电容值的分布，电阻值应相等。

对于相等的电阻值，Q 的公式简化为

重新排列这个方程，得到C2的C4，

我们可以将此表达式代入等式中：

n（公式 1b）并求解 C4：

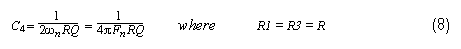
将此结果代入 C2 的方程（公式 7），我们得到

简化的设计流程

将Sallen-Key滤波器增益设置为单位并设置R1 = R3，可通过求解两个简单方程来设计低灵敏度单运放滤波器。简化的设计过程如下：

选择合适的电阻值。

使用公式8和9求解电容值。

如果C2太大，则从较大的电阻值重新开始。

如果C4太小，则从较小的电阻值重新开始。

如果 C4 太小而 C2 太大，则您已达到 此筛选器的限制。

选取最接近计算值的标准值。

两个例子说明了这种方法及其使用所带来的好处。

将新方法与食谱方法进行比较

第一个例子来自作者几年前所做的工作。为了尽量减少生产中的电路变化，他重新设计了一个电路（最初是用食谱技术创建的），以实现频率为-3dB的4.8kHz的三阶巴特沃兹低通滤波器。重新设计消除了修剪锅及其相关的调整需求。

该滤波器需要一个Q = 1、固有频率为4.8kHz的二阶级。它最初采用Sallen-Key拓扑结构和参考文献2第156至157页的设计方法实现，该方法将电阻值设置为相等（R1 = R3 = R），电容值相等（C2 = C4 = C）。选择 C = 0.001μF 会导致增益 （K） = 2 和 R = 33.2K。该电路的Q灵敏度如下：

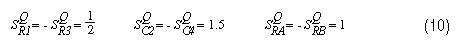
滤波器采用我们的新方法重新设计，使用相同的电阻值（33.2kΩ）。等式8和9得出C2 = 2000pF和C4 = 500pf。灵敏度如下：

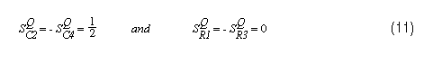
图2显示了用于仿真这些电路的原理图，图3显示了SPICE仿真的结果。这些频率响应图是每个滤波器使用100%容差电阻和1%电容对每个滤波器进行5种不同“构建”的蒙特卡罗运行的结果。对于每个“构建”，SPICE 模拟器在其指定的公差范围内随机改变组件值。请注意，对于通带中的所有频率（尤其是接近固有频率的频率），新滤波器的变化明显小于旧滤波器。

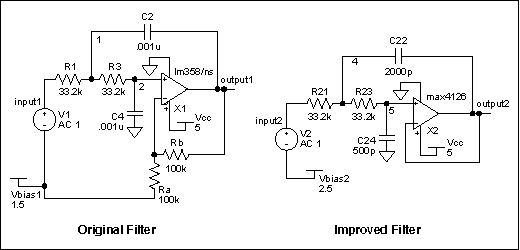
图2.

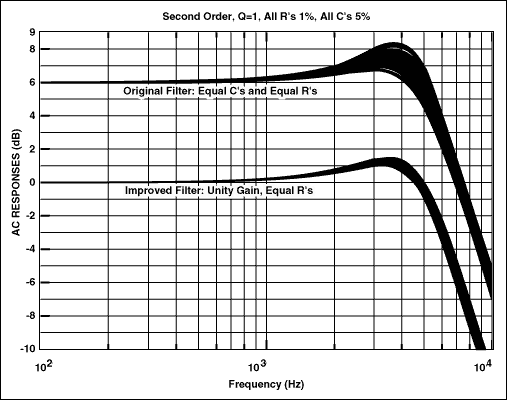
图3.

同样重要的是要注意，这些仿真结果并不是证明电路运行所需的唯一步骤;您还应该构建和测试电路。一旦SPICE仿真器指示交流性能与标称元件值的实际电路相同，您就可以使用SPICE仿真器中常见的蒙特卡罗函数来评估电路响应如何随元件的变化而变化。

级联级实现高阶滤波器

单位增益Sallen-Key方法有两个缺点。它不能提供增益，对于高Q值滤波器，其电容比可能太大，无法实现滤波器。现有的放大器级通常可以提供所需的增益;但是，如果没有，最坏的解决方案是增加一个单运放增益级。

高阶滤波器通常需要至少一个具有非常高Q值的级。该级可以使用更复杂的拓扑来实现，而其他级则使用低灵敏度Sallen-Key电路实现。即使有Q值限制，Sallen-Key拓扑也可以执行传统上使用多运算放大器拓扑实现的高阶滤波器。以下示例显示了设计此类筛选器的新过程，演示了与旧方法相比性能的显著提高。标称规格如下：

七阶切比雪夫

0.05dB纹波

8kHz -3dB 频率

增益 = 10

从这些客观规范中实际推导传递函数超出了本文的范围，但参考文献详细介绍了该主题。传递函数有三个复极对和一个简单极点：

 

Fn	Q
7.834千赫	5.5662
6.560千赫	1.6636
4.492千赫	0.7882
3.162千赫	简单

 

该滤波器的两个版本的原理图如图4所示。一个是用食谱方法设计的，另一个是用我们的新方法设计的。每个电路最后级的单个运算放大器提供所需的增益和第七极。

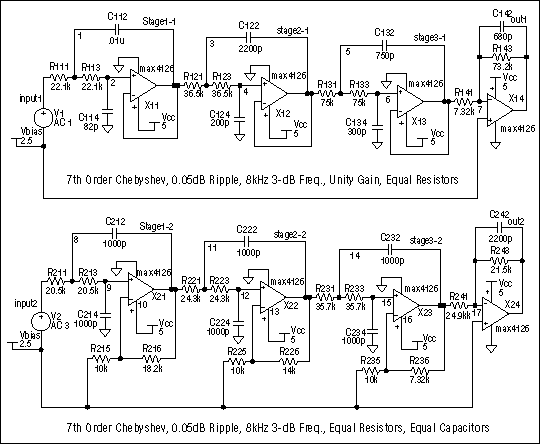
图4.

图5显示了使用1%电阻和5%电容的蒙特卡罗分析结果。为了视觉清晰，结果在图表上偏移。食谱版本在固有频率附近具有大约28dB的变化，使该设计毫无用处。相比之下，单位增益/均阻版本在谐振附近的增益变化仅为4dB。

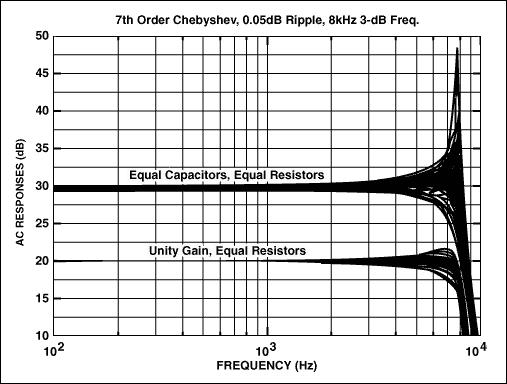
图5.

萨伦基与双二阶滤波器

将这种七阶Sallen-Key电路与相同传递函数的多运算放大器实现进行比较是很有趣的。双二阶滤波器是一种非常常见的三运放滤波器，具有低灵敏度和简单的设计公式。其原理图如图6所示。使用参考文献2中描述的技术，灵敏度如下：

 

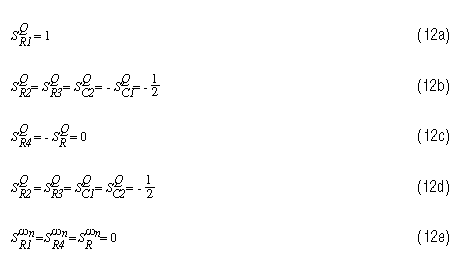
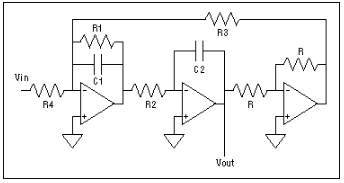
图6.

我们规范的双二阶实现原理图如图7所示。同样，末端的单运放级执行增益和第七个极点。图8比较了单位增益Sallen-Key和双二阶实现的蒙特卡罗分析的频率响应（为了清楚起见，结果再次偏移）。对于等效的组件，这两个滤波器之间的性能没有显著差异。事实上，Sallen-Key的低频增益变化略小于双二阶。

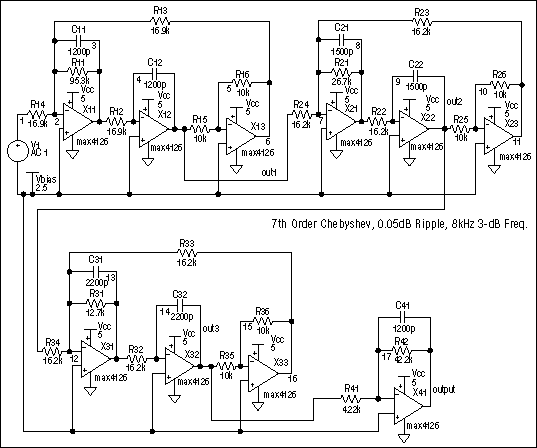
图7.

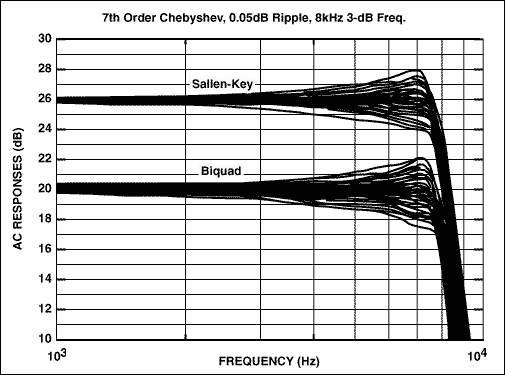
图8.

下表列出了刚才讨论的七阶滤波器的三种实现方案的元件数、通带变化和电容值的扩散：

 

电路	通带变化	运算放大器	电阻	电容器	电容扩散
统一增益 S-K	4分贝	4	8	7	从窄到宽
相等的遥控 S-K	28分贝	4	14	7	窄
双四体	4分贝	10	20	7	窄

 

将这些技术扩展到高通滤波器

我们还可以使用这些技术设计低灵敏度高通滤波器。等效的Sallen-Key高通滤波器如图9所示。

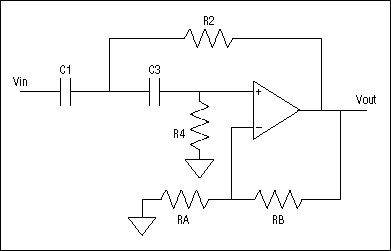
图9.

其设计公式和灵敏度如下：

至于低通情况，我们可以通过设置 K = 1 和（在本例中）将电容器值设置为相等来简化。然后，方程简化为：

结果是电阻的两个简单公式，其中C1 = C2 = C：

因此，高通设计过程与低通情况非常相似：

为 C 选择适当的值。

使用公式15a和15b计算电阻值。

如果 R4 太大，请使用较大的 C 值重新开始。

如果 R2 太小，请使用较小的 C 值重新开始。

如果 R2 太小而 R4 太大，则您已达到 此类型筛选器的限制。

选取最接近计算值的标准值。

为了说明这一过程，我们可以设计一个Q为1.0、固有频率为8.0kHz的二阶高通滤波器级。首先，选择 C = 1200 pF。接下来，使用公式15a和15b设置电阻值：R2= 8.25kΩ 和 R4= 33.2kΩ。频率响应与前面讨论的低通滤波器的频率响应一起绘制（图 10）。

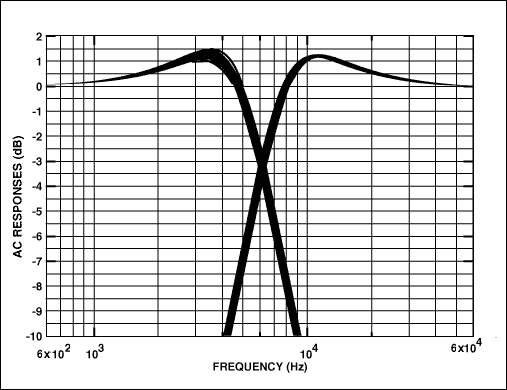
图10.

高通滤波器的频率响应扩散比低通滤波器更窄，特别是在峰值附近。这是因为我们最大限度地降低了对变化最大的元件（电容器）的敏感性。对于低通情况，对电阻的Q灵敏度最小，对电容的灵敏度为1/2。对于高通情况，对电阻的灵敏度为1/2，对电容的灵敏度降至最低。我们使用1%电阻和5%电容，因为低容差电阻比低容差电容更容易获得。如果选择5%电阻，则两个电路的分布相似。

结论

通过更深入地研究Sallen-Key滤波器的元件灵敏度，我们在数学描述中发现了一个“最佳点”，允许设计简单的单运算放大器滤波器，其性能可与更复杂的滤波器相媲美。这种方法有助于将Sallen-Key滤波器的效用扩展到高阶高Q值滤波器的效用，并且对其他拓扑的类似研究可能会产生类似的结果。

审核编辑：郭婷