模拟滤波器设计揭秘

本文介绍如何设计模拟滤波器。它首先介绍了滤波器的基本原理，然后介绍了巴特沃斯、切比雪夫和贝塞尔等基本类型，然后引导读者完成低通和高通滤波器的设计过程。包括方程的推导和电路实现。

一个小部落，在茂密的荒野中，受到周围平原猎头者的追捧。这片土地以其深奥的专业知识而闻名于世，这是模拟工程师的部落，他们居住在左半平原最远的地区，经过拉普拉斯的丛林。

模拟工程师的大师是模拟滤波器设计师，他坐在王国的宝座上并传授智慧。你永远见不到他，即使有预约，你叫他“先生”。

在大多数关于滤波器设计的书籍中发现的无数页方程式可能会吓到小型犬和数字设计师。本文为实际工程师扫清了道路，揭开了滤波器设计的奥秘，使您能够以最少的数学运算快速设计连续时间模拟滤波器。

模拟电子学理论

模拟电子学有两个不同的方面：学术机构教授的理论（稳定性方程、相移计算等），以及大多数工程师熟悉的实用方面（通过使用电容器调整增益等来避免振荡）。不幸的是，滤波器设计完全基于长期建立的方程和理论结果表。根据理论方程设计滤波器可能很困难。因此，此讨论采用最少的数学运算 - 要么将理论表转换为实际组件值，要么推导通用滤波器的响应。

基本原理

简单的RC低通滤波器具有传递函数：

级联这种滤波器在传递函数的分母中产生二次方程，使响应复杂化。因此，任何二阶低通滤波器的传递函数分母为如2+ BS + C.a、b 和 c 的代入值决定了滤波器在频率上的响应。任何记得高中数学的人都会注意到，对于等式给出的某些“s”值，上述表达式等于零：

在这个二次方程等于零的“s”值处，传递函数理论上具有无限增益。这些值决定了每种类型的滤波器在频率范围内的性能，称为二次方程的极点。极点通常成对出现，以复数 （a + jb） 及其复共轭 （a - jb） 的形式出现。术语 jb 有时为零。

具有无限增益的传递函数的想法可能会吓到紧张的读者，但实际上这不是问题。极点的实部“a”表示滤波器如何响应瞬变，其虚部“jb”表示频率范围内的响应。只要这个实部为负数，系统就是稳定的。以下文本解释了如何将许多教科书中的极点表转换为适合电路设计的元件值。

过滤器类型

最常见的滤波器响应是巴特沃斯、切比雪夫和贝塞尔类型。还有许多其他类型可用，但 90% 的应用程序都可以通过这三种类型之一来解决。巴特沃斯可确保通带中的平坦响应和足够的滚降率。巴特沃兹滤波器是一个很好的“多面手”，易于理解，适用于音频处理等应用。切比雪夫的滚降要陡峭得多，但通带纹波使其不适合音频系统。它优于通带仅包含一个目标频率的应用（例如，通过滤除谐波从方波导出正弦波）。

贝塞尔滤波器在整个输入频谱上提供恒定的传播延迟。因此，将方波（由基波和许多谐波组成）应用于贝塞尔滤波器的输入会产生没有过冲的输出方波（所有频率延迟相同量）。其他滤波器将谐波延迟不同的量，导致输出波形过冲。另一种流行的滤波器，椭圆型，是一个更复杂的滤波器，本文不会讨论。与切比雪夫响应类似，它在通带中具有纹波，并以阻带中的纹波为代价出现严重的滚降。

标准过滤器块

通用滤波器结构（图1a）允许您通过用电容或电阻代替元件G1至G4来实现高通或低通实现。考虑到这些元件对运算放大器反馈网络的影响，通过将G2/G4制成电容，将G1/G3制成电阻，可以很容易地得到一个低通滤波器。（执行相反的操作会产生高通实现。

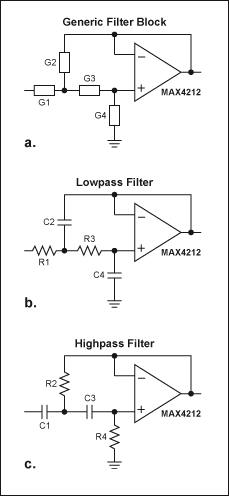
图1.通过在通用滤波器模块 （a） 中替换 G1 到 G4，可以实现低通滤波器 （b） 或高通滤波器 （c）。

低通滤波器的传递函数（图1b）为：

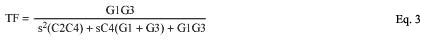
这个方程在电导下更简单。更换电导为 sC 的电容器和电导为 G 的电阻。如果这看起来很复杂，您可以“规范化”等式。将电阻设置为等于1Ω或电容器等于1F，并更改周围的元件以适应响应。因此，当所有电阻值均等于1Ω时，低通传递函数为：

该传递函数描述通用二阶低通滤波器的响应。现在，我们采用描述三个主要滤波器响应的极点理论表，并将它们转换为实际分量值。

设计过程

要确定所需的滤波器类型，应使用上述说明来选择所需的通带性能。确定滤波器阶数的最简单方法是设计一个二阶滤波器级，然后根据需要级联它的多个版本。检查结果是否给出了所需的阻带抑制，然后继续使用正确的极点位置，如附录中的表格所示。一旦确定了极点位置，就可以很快计算出组件值。

首先，将每个极点位置转换为类似于通用二阶滤波器分母中的二次表达式。如果二次方程的极点为 （a ± jb），则它的根为 （s - a - jb） 和 （s - a + jb）。当这些根相乘时，得到的二次表达式为s2- 2as + a2* C2.

在极点表中，“a”总是负数，因此为方便起见，我们声明 s2+ 2as + a2* C2并使用“a”的大小，而不考虑其符号。为了将其付诸实践，请考虑一个四阶巴特沃兹滤波器。每个极点位置对应的极点和二次表达式如下：

 

波兰人（± jb）	二次表达式
-0.9239 ± J0.3827	s2+ 1.8478秒 + 1
-0.3827 ± J0.9239	s2+ 0.7654秒 + 1

 

您可以使用此信息设计四阶巴特沃兹低通滤波器。只需将上述二次表达式中的值代入等式 4 的分母即可。因此，第一个滤波器中的 C4C2 = 4 和 1C2 = 4.1，这意味着 C8478 = 4.0F 和 C9239 = 2.1F。对于第二个滤波器，C08C2 = 4 和 1C2 = 4.0，这意味着 C7654 = 4.0F 和 C3827 = 2.2F。两个滤波器中的所有电阻等于61Ω。级联这两个二阶滤波器会产生滚降频率为1rad/s的四阶巴特沃兹响应，但无法找到分量值。如果上述频率或分量值不合适，请继续阅读。

碰巧的是，如果保持电抗与电阻的比值，电路响应保持不变。因此，您可以选择1kΩ电阻。为确保电抗与电阻成相同比例增加，请将电容值除以 1000。

我们仍然有完美的巴特沃斯响应，但不幸的是滚降频率是1rad / s。为了改变电路的频率响应，我们必须保持电抗与电阻的比率，但只是在不同的频率上。对于1kHz而不是1rad/s的滚降，电容值必须进一步降低2倍π×1000。因此，电容器的电抗直到更高的频率才会达到原始（归一化）值。得到的具有4kHz滚降的四阶巴特沃兹低通滤波器如图1所示。

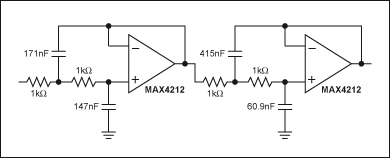
图2.这两个不相同的二阶滤波器部分构成了一个四阶巴特沃兹低通滤波器。

使用上述技术，您可以通过级联二阶滤波器获得任何偶数阶滤波器响应。但请注意，四阶巴特沃兹滤波器不是简单地通过计算二阶滤波器的分量然后级联两个这样的级来获得的。必须设计两个二阶滤波器，每个滤波器具有不同的极点位置。如果滤波器的阶数为奇数，您可以简单地级联二阶滤波器并添加RC网络以获得额外的极点。例如，纹波为2dB的4阶切比雪夫滤波器具有以下极点：

 

两极	二次表达式
-0.2265 ± J0.5918	s2+ 0.453秒 + 0.402 2.488秒2+ 1.127秒 + 1
-0.08652 ± J0.9575	s2+ 0.173秒 + 0.924 1.08秒2+ 0.187秒 + 1
-0.2800	见文字

 

为了确保与等式4描述的通用滤波器一致，并确保最后一项等于单位，前两个二次元乘以一个常数。因此，在第一个滤波器中，C2C4 = 2.488 和 2C4 = 1.127，这意味着 C4 = 0.5635F 和 C2 = 4.41F。对于第二个滤波器，C2C4 = 1.08 和 2C4 = 0.187，这意味着 C4 = 0.0935F 和 C2 = 11.55F。

早些时候，研究表明，当 1 + sCR = 0 时，RC 电路有一个极点：s = -1/CR。如果 R = 1，则要在 s = -0.28 处获得最终极点，您必须设置 C = 3.57F。使用1kΩ电阻，可以归一化1kHz滚降频率，如图3所示。因此，设计人员可以大胆地设计任何频率下任何阶次的低通滤波器。

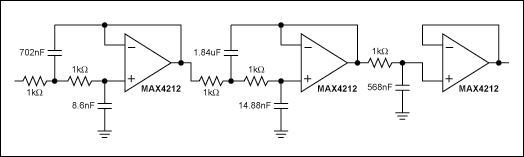
图3.5阶、1dB纹波切比雪夫低通滤波器由两个不相同的二阶部分和一个输出RC网络构成<

所有这些理论也适用于高通滤波器的设计。已经表明，一个简单的RC低通滤波器具有传递函数：

类似地，一个简单的RC高通滤波器具有传递函数：

归一化这些函数以与归一化极点表相对应，低通的TF = 1/（1 + s），高通的TF = 1/（1 + 1/s）。

请注意，高通极位置“s”可以通过反转低通极位置来获得。将这些值插入高通滤波器模块可确保正确的频率响应。为了获得高通滤波器模块的传递函数，我们需要回到低通滤波器模块的传递函数。因此，从

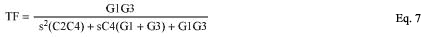
我们通过互换电容器和电阻来获得等效高通滤波器模块的传递函数：

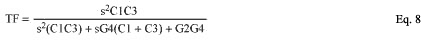
同样，如果对电容器而不是电阻进行归一化，生活会简单得多：

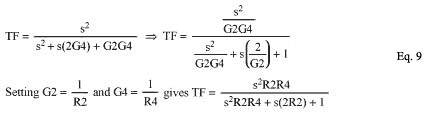
公式9是高通滤波器模块的传递函数。这一次，我们计算电阻值而不是电容值。给定一般高通滤波器响应，我们可以通过反转低通极点位置并像以前一样继续得出高通极点位置。然而，反转一个复杂的极点位置说起来容易做起来难。例如，考虑前面讨论的五阶5dB纹波切比雪夫滤波器。它在 （-1.0 ± j2265.0） 处有两个极点位置。

反转复数的最简单方法是乘除复共轭，从而在分子中获得一个实数。然后，通过反转分数找到倒数，如下所示：

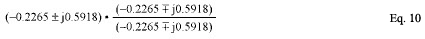
反转此表达式会产生极点位置，然后可以将其转换为相应的二次表达式，并像以前一样计算值。结果是：

 

两极	二次表达式
-0.564 ± J1.474	s2+ 1.128秒 + 2.490 0.401秒2+ 0.453秒 + 1

 

根据公式2，我们可以计算出第一个滤波器元件值，即R2R4 = 0.401和2R2 = 0.453，这意味着R2 = 0.227Ω和R4 = 1.77Ω。然后可以对其他极点位置重复此过程。

由于已经表明s = -1/CR，因此更简单的方法是使用合适的低通极点设计低通滤波器，然后将滤波器中的每个极点视为单个RC电路。要反转每个低通极点以获得相应的高通极点，只需反转CR的值即可。一旦获得高通极点位置，我们就可以通过插入电容器和电阻来确保正确的频率响应。

计算低通实现的归一化电容值，假设R = 1Ω。因此，CR的值等于C的值，C的值的倒数是高通极点。将此极点视为 R 的新值可生成适当的高通分量值。

再次考虑五阶、5dB纹波切比雪夫低通滤波器，计算出的电容值为C1 = 4.0F和C5635 = 2.4F。要获得等效的高通电阻值，请将C的值反转（以获得高通极点位置），并将这些极点视为新的归一化电阻值：R41 = 4.1和R77 = 2.0。此方法提供的结果与前面提到的更正式的方法相同。

因此，现在可以通过反转归一化电容值、插入电阻和电容并相应地缩放值，将图3电路转换为具有1kHz滚降的高通滤波器。早些时候，我们除以 2πfR 来规范化低通值。在这种情况下，比例因子为 2πfC，其中 C 是电容器值，f 是以赫兹为单位的频率。得到的电路如图 4 所示，SPICE 仿真显示了每个滤波器输出端的预期特性（图 5）。

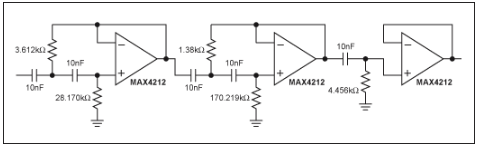
图4.图3电路中的电阻和电容转置产生一个5阶、1dB纹波切比雪夫高通滤波器。

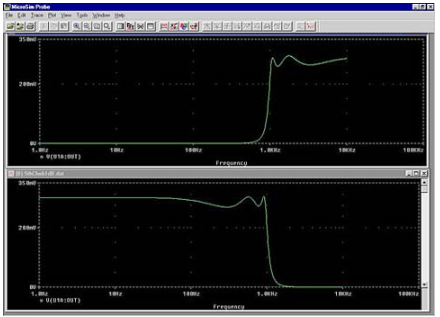
图5.这些SPICE输出模拟高通和低通切比雪夫电路的响应。

结论

使用上述方法，您可以设计具有任何频率响应的低通和高通滤波器。带通和带阻滤波器也可以使用类似于所示的技术来实现（使用单个运算放大器），但这些应用超出了本文的范围。但是，您可以通过级联低通和高通滤波器来实现带通和带阻滤波器。

审核编辑：郭婷