通信系统中抖动简介

本抖动简介介绍了各种抖动类型的定义，包括随机抖动类型：高斯、周期间、相邻周期;和确定性抖动类型：占空比失真、脉冲宽度失真、脉冲偏斜和数据相关（模式）抖动。应用笔记还讨论了各种抖动元件与系统误码率（BER）之间的关系。

什么是抖动？

SONET标准指出，“抖动被定义为数字信号的重要时刻从其理想位置在时间上的短期变化。重要时刻可能是（例如）最佳采样时刻。光纤通道标准简单地将抖动定义为“与事件理想时间的偏差”。

简而言之，术语“抖动”描述了系统内的时序错误。在通信系统中，抖动的累积最终会导致数据错误。

对系统用户最有价值的参数是这些数据错误的发生频率，通常称为误码率（BER）。稍后我们将更详细地讨论 BER。

首先，一些定义。基本抖动类型和定义如下表1所示。一些抖动类型有许多常用术语来描述相同的测量。其他术语描述了同一抖动类型的不同测量方法。如果使用多个术语来描述相同的抖动类型，则这些术语将一起列出。

 

抖动项	定义	附加信息
抖动	除了上述定义外，抖动还由两种基本类型组成：随机和确定性。
随机抖动 （RJ）	无界抖动，可以用高斯概率分布来描述。随机抖动的特征在于其标准偏差（rms）值。	主要来源是系统组件中的高斯（白色）电噪声。电噪声与信号的压摆率相互作用，在开关点产生时序误差。
随机	RJ测量方法。基于实际时钟边沿与其理想（预期）位置之间的时间差的概率分布。	尽管同一源的两个测量值，但随机和周期间抖动并不等效。周期间抖动具有频率相关项，与随机抖动测量相比，将加重高频抖动源，同时抑制低频源。随机抖动测量与频率无关。
循环到循环相邻循环	RJ测量方法。基于一个时钟周期和相邻周期之间测量的周期差的概率分布。
确定性抖动 （DJ）	具有非高斯概率密度函数的抖动。总是有幅度和特定原因的限制。DJ的特点是其有限的，峰到峰的价值。	源通常与设备或传输介质行为的缺陷有关，但也可能是由于EMI、串扰、接地问题。
占空比失真 脉冲宽度失真 脉冲偏斜	DJ 组件。占空比值与理想（预期）值的偏差。在许多串行数据系统中，这相当于1位和0位之间的位时间偏差。也可以定义为低到高和高到低延迟时间之间的传播延迟差异。	源通常是系统内上升沿和下降沿之间的时序差异。也可能是由单端系统中的接地偏移引起的。
数据相关抖动模式抖动 码间干扰	DJ 组件。计时错误因使用的数据模式而异。数据相关和码型抖动用于描述抖动在时域中的影响。码间干扰更常应用于频域测量，即频谱分析仪上看到的信号峰值的扩展。	主要来源是组件和系统带宽限制。高频信号的建立时间比低频信号短。这会导致不同频率下转换的起始条件发生变化，并产生取决于所应用数据模式的时序误差。
正弦抖动 周期性抖动	DJ 组件。具有正弦（或周期性）形式且与数据模式相关（相关）的抖动。	源是来自与数据模式相关的信号的干扰。接地反弹和其他电源变化是常见原因，尽管通常遇到的正弦抖动水平非常低。
不相关的有界抖动	DJ 组件。有界抖动 振幅和不相关（与数据模式）。	通常为正弦信号源，是来自系统内部或外部其他信号源的干扰。源包括 EMI、电容和电感耦合以及电源开关噪声。
总抖动 （万亿焦耳）	确定性和随机抖动的总和（或卷积）。总抖动是获得的峰峰值。	TJ = DJ + n × RJ 其中 n = 对应于所需 BER 的标准差数。由于它很简单，通常应用此求和，尽管这种方法高估了实际 BER，因为最大 RJ 误差并不总是与最大 DJ 误差一致。两种抖动类型的概率（卷积）求和将产生更准确的解决方案，尽管应用它需要了解 DJ 调制波形。
映射抖动	DJ 类型的系统级抖动分量。在映射过程中发生位填充时，由于数据从一个传输标准映射到另一个传输标准而导致的抖动。	去映射后，恢复的信号中会留下间隙。锁相环（PLL）用于平滑产生的间隙，但仍存在一定量的抖动。
指针抖动	DJ 类型的系统级抖动分量。由于将包含定义的指针活动序列的 SONET 信号应用于解复用器而导致抖动。
徘徊抖动	系统级抖动分量 DJ类型。频率小于 10Hz 的低频定时误差 （SONET）。	主要来源是系统温度变化。
抖动传输 抖动增益	输出信号上的抖动与输入信号上的抖动之比。	用于量化数据重定时器件（再生器、PLL）的抖动累积性能。
抖动容限	接收器在不违反系统BER规范的情况下必须容忍的输入抖动量。	可分为随机抖动容限和确定性抖动容限。
单位间隔 （UI）	相当于串行数据流中 1 位时间的时间段。	波特率的倒数。抖动规格通常以 UI 的倍数引用。

 

抖动如何导致数据错误？

通过在特定时刻对数据信号进行采样，从串行数据流中提取信息。理想情况下，这些采样时刻始终发生在数据位时间的中心，在两个相邻的边沿转换点之间等距。抖动的存在会改变相对于采样点的边沿位置。然后，当数据边位于采样时刻的错误一侧时，将发生错误。

如表1所述，总抖动可以表示为确定性抖动和任何特定误差概率值下随机抖动的标准差数之和。随机抖动在上面定义为抖动，可以用高斯概率分布来描述。高斯分布是围绕平均值对称的。一个标准差 （1σ） 定义为包含 68.26% 总体到均值一侧的窗口。表2列出了σ的倍数，并列出了适用于每个倍数的总人口比例。

 

限制	限量内人口比例
±1秒	68.2689%
±2秒	95.45%
±3秒	99.73%
±4秒	99.99367%
±5秒	99.9999427%
±6秒	100-1.973 × 10-7%
±7秒	100-2.5596 × 10-10%
±8秒	100-1.24419 × 10-13%
±9秒	100-2.25718 × 10-17%
±10秒	100-1.53398 x 10-21%

 

确定性和随机抖动求和的结果是另一种概率分布，其示例如图1所示。该分布绘制概率与时序误差幅度的关系图，其特征在于具有表示确定性抖动成分的中心部分和作为（随机抖动）高斯分布尾部的外部部分。所示的分布形状称为双峰响应。

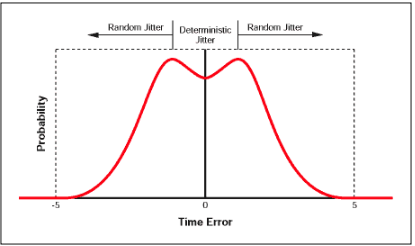
图1.显示确定性和随机分量的概率直方图。

将图1所示的抖动概率分布添加到数据流中，可以有效地调制相对于采样时刻的数据边沿位置。如图 2 所示，它显示了叠加在数据转移点上的概率直方图的理想眼图。与采样时刻相关的数据错误的概率是第一个数据转换到达得太晚或第二个数据转换到达得太早的概率之和。该概率由图 2 中采样点曲线下方的阴影部分表示。

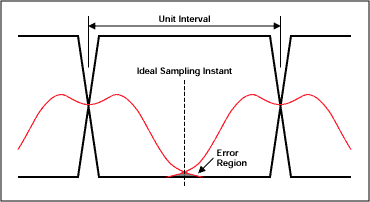
图2.具有数据转换时间概率直方图的理想眼图。

要找到发生数据错误的概率，必须将任一数据边出错的概率之和乘以实际发生转换的概率。后者由平均转换密度表示，并假设等于典型数据流的 50%。

举个例子，考虑一个总确定性抖动为0.3UIp-p（包括所有非高斯时序误差源）和0.05UI rms随机抖动的数据流。最大允许抖动为1UIp-p;这是理想接收器在发生错误之前可以容忍的抖动量（请参阅下面的注释）。使用公式 1 的表达式

DJ（pk） + n × RJ（rms） = TJ（pk）

代入TJ = 0.5UI（pk），DJ = 0.15UI（pk）和RJ = 0.05UI（rms），我们得到n = 7。这是将产生数据错误的随机抖动的标准差 （σ） 数。对于高斯分布，1.28 × 10-10% 的样本位于均值一侧的 7σ 限制之外。总误差率（BER）由公式2给出。

误码率 = （1.28 × 10−10% + 1.28 × 10−10%) × 50% = 1.28 × 10-10%

等式 2 的结果对应于 1.28 × 10 的 BER−12.

对应于±1σ至±10σ的随机抖动限值的误码率见下表3。

 

限制	大约
±1秒	0.16
±2秒	2.28 × 10-2
±3秒	1.35 × 10-3
±4秒	0.32 × 10-4
±5秒	2.87 × 10-7
±6秒	0.98 × 10-9
±7秒	1.28 × 10-12
±8秒	0.62 × 10-15
±9秒	1.13 × 10-19
±10秒	0.77 × 10-23

 

注意：特定BER值下允许的最大抖动通常由系统规格或要求系统兼

审核编辑：郭婷