如何使用Laplace方程仿真滤波器和运算放大器？

什么是 Laplace？

在 LTspice 的 Voltage-controlled Voltage Source 中，可以使用 Laplace (拉普拉斯) 变换对传递函数。通过构建电压源的微分方程式，仿真各种各样的等价模型。

用 Laplace 仿真一阶低通滤波器

首先，在 “Select Component Symbole” 对话框中选择 “e”，并将其放在电路图上。如下图 (图1) 所示

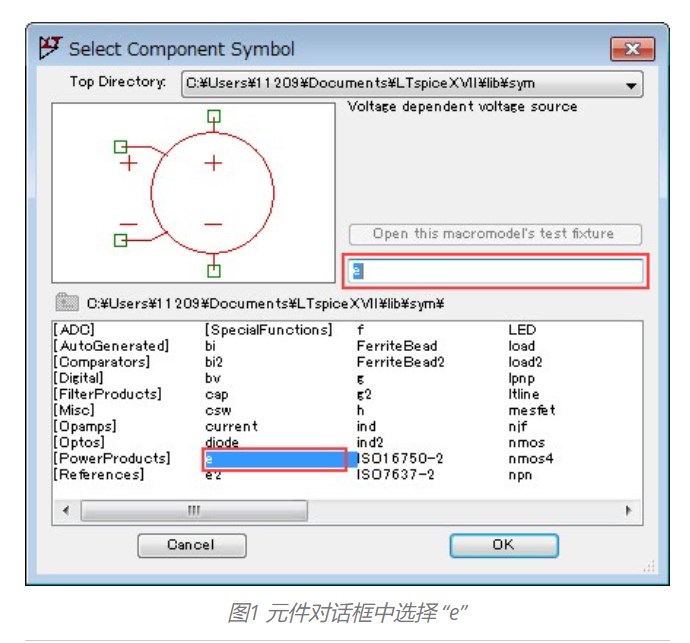
将光标悬停在组件 (E1) 处单击鼠标右键，或在字母 “E” 上右键点击以打开编辑器。一阶低通滤波器的传递函数为一阶延迟元素，因此用 “1/(1+TS)” 表示。这里将截止频率设定为 fc=1.59kHz。因此，可以计算 “T=1/(2*pi*fc)=100e-6”， 在 “Value” 处输入方程 “Laplace=1/(1+100e-6*s)”，如下图 (图2) 所示：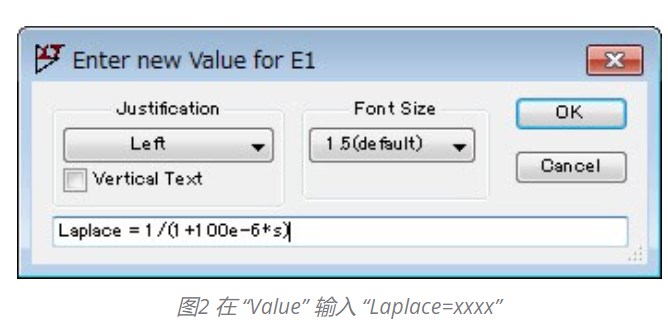



电路图如下图 (图3) 所示设定，通过 AC 分析确认频率特性后，观测到截止频率约为 1.59Hz。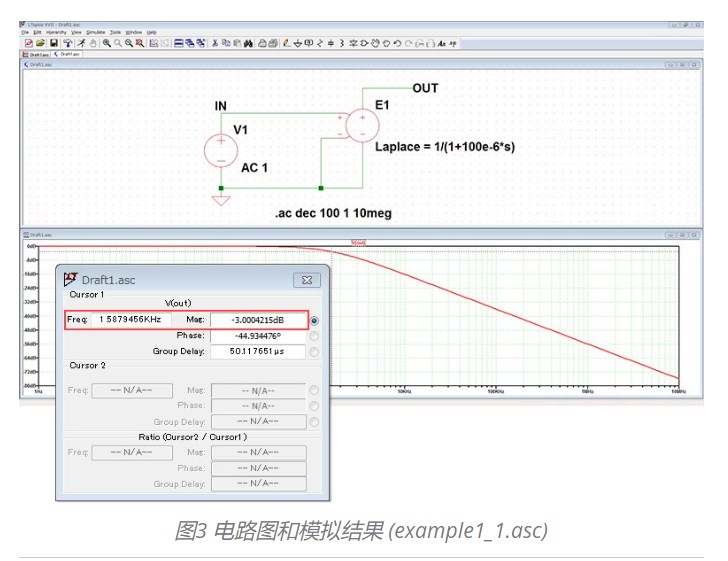



另外，使用电阻 (R) 和电容器 (C) 的组件，仿真截止频率为 fc=1.59Hz 的一阶低通滤波器，模拟结果如下图 (图4) 所示。像这样，通过使用 Laplace 方程代替由零件组件，可以活用数学模型进行模拟。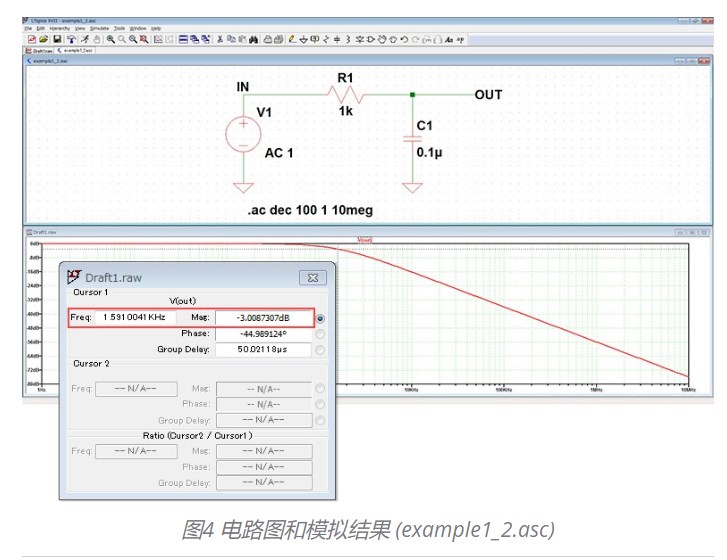

用 Laplace 仿真运算放大器模型

试着仿真开环增益 100dB (10^5 倍)，单位增益 10MHz (GB 积=10MHz)，且不考虑偏移等规格，只设定放大率和频带的简易放大器模型。

运算放大器的传递函数 (G) ，由放大系数 (A) 和一阶延迟的元素 (1+TS) 可表示为 “G=Vout/Vin=A/(1+TS)”。A 是 100dB，所以设为 1e5。另外，T 由 GBW 求得。 可以计算出截止频率 fc 为 GBW/A=10MHz/1e5=100Hz，因此最终得出 T=1/(2*pi*Fc)=0.00159。

最后，使用 Laplace 方程在公式中填写 “Laplace=1e5/(1+0.00159*s)”，并运行下图 (图5) 的仿真模拟。如 AC 分析结果所示，这样 GBW=10MHz 的简易运算放大器就仿真完成了。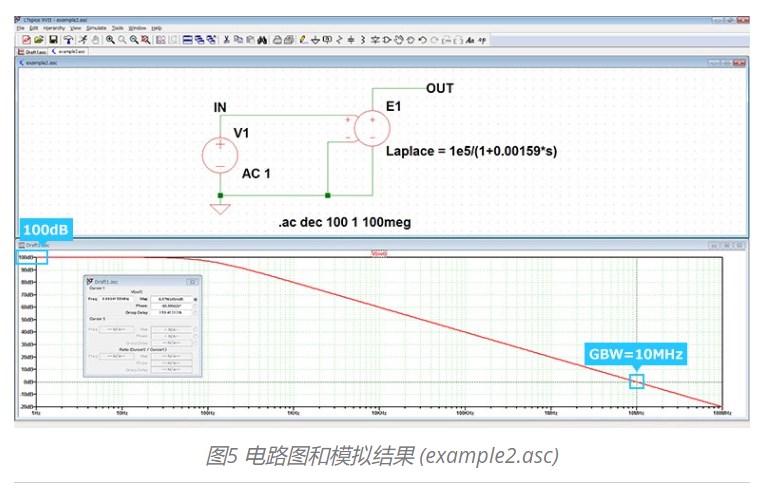

总结

本文介绍了如何使用 Laplace 方程仿真滤波器和运算放大器。其实 Laplace 方程不仅可以应用于放大器、滤波器设计，还可以应用于控制系统设计、电机建模以及结合电子电路等分析。

审核编辑：刘清