

偶数阶勒让德滤波器的设计介绍
EMC/EMI设计
描述
这篇文章推导了偶数阶勒让德滤波器(L滤波器, Pupoulis滤波器)的设计,方法几乎和Pupoulis的一模一样,但是作为Pupoulis滤波器的补充是非常有必要介绍本篇论文的。
Optimum Filters of Even Orders with Monotonic Response*
偶数阶单调响应的最优滤波器*
MINORU FUKADA
自从收到本文后,Pupoulis关于同一问题的类似解决方案已经作为一封给编辑的信件出现在IRE的会议记录中。尽管Fukada在提交他的论文时并不知道这个先前的公开信息,但是因为Fukada的处理包含了更多的细节并且包括了计算响应曲线,我们决定它仍然值得发表。—编辑
引言
PAPOULIS开发了一类新的滤波器(滤波器),在单调递减的频响下具有最大截止率。这类滤波器在阻带中的衰减比同阶的Butterworth滤波器更大,但由于其频率响应中的单调性质,它仍然保持了尚可的时域响应。Papoulis给出了奇数阶(odd degree)最优多项式的公式,从中推导出这些滤波器。本文的目的是给出偶数阶(even degree)最优多项式的一般公式,并表明从这些多项式中,滤波器实际上是可以被实现出来的。
偶数阶的滤波器
一个没有有限零点的滤波器的幅度特性可以写成以下形式:
其中是一个在上的阶数为,且有实系数的多项式。如果随着的增加而单调增加,那么的单调性要求就可以被满足。因此,滤波器的问题是确定一个在上的阶数为的正递增多项式,使得在点的斜率最大。数学上,我们可以通过以下等式来定义这个问题:
以及是最大的。
对于奇数的,解已经由Papoulis给出;因此,下面的讨论将仅限于偶数的
其中,由在截止频率处的指定衰减所定。网络函数可以通过常规方法确定。设为幅度等于的网络函数。然后我们有
从中我们获得了左半平面极点的。参考图3的情况,我们有
从这个关系式我们得到,并将连分数展开,我们获得无耗梯形网络实现。在下面的例子中,我们将取,使得在处产生的衰减。
特殊情况
由公式(7)我们得到
因此,由公式(6)我们得到
这表明二阶的滤波器退化为滤波器(译注:这里指Butterworth滤波器)。
由公式(8)和公式(6)我们得到,
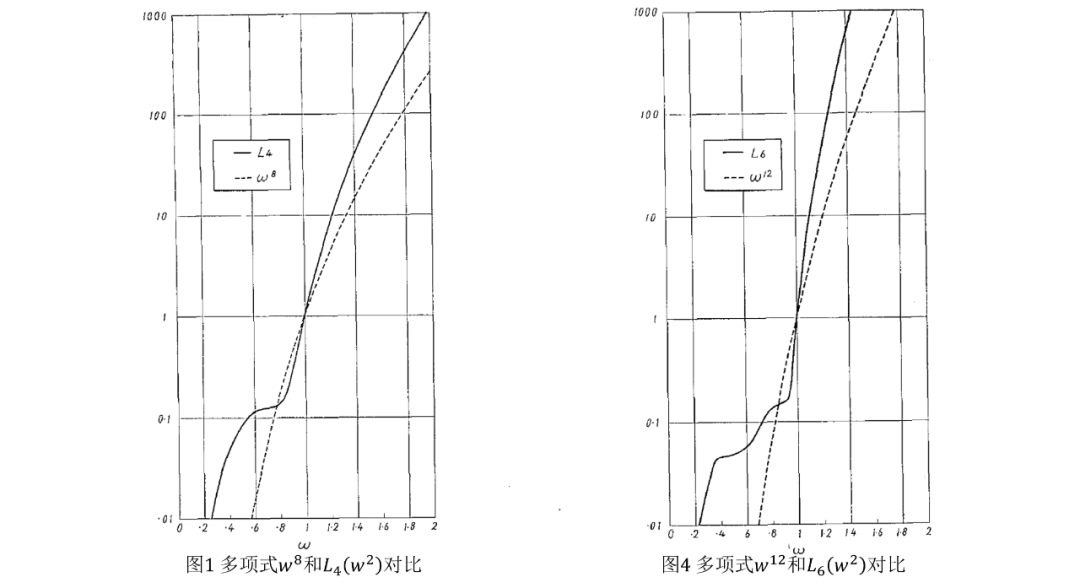
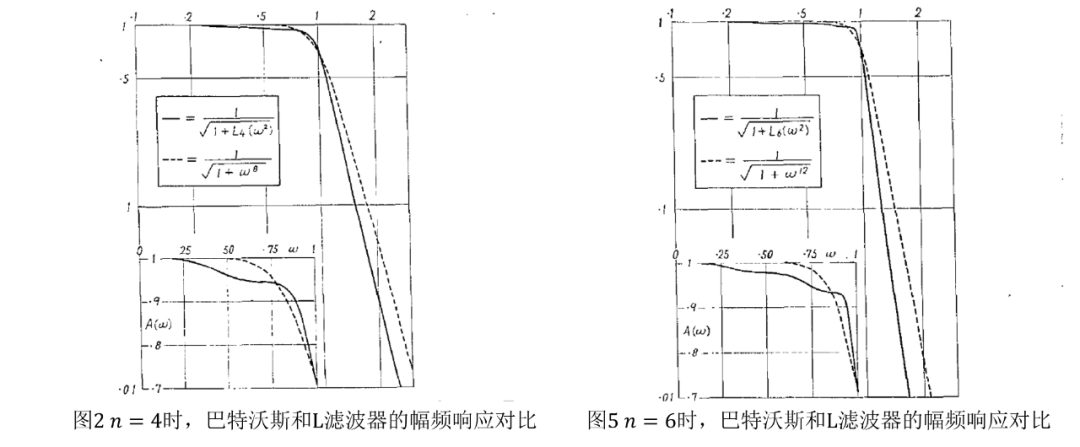
多项式及其结果的幅频响应分别在图1和图2中绘制。的极点由下式给出
从中我们得到
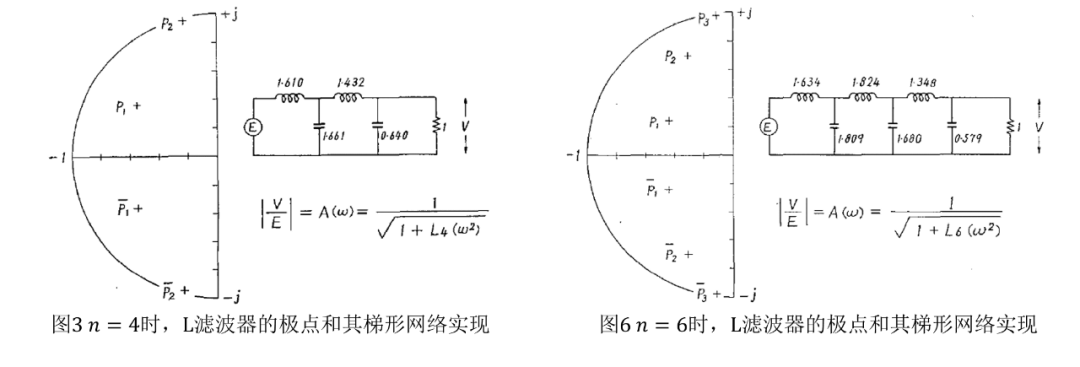
的极点和梯形网络实现如图3所示。
因此,
多项式及其结果的幅度响应分别在图4和图5中绘制。的极点由下式给出
从中我们得到
其中,
的极点和梯形网络实现如图6所示。
到
结合Papoulis的结果和这里提供的结果,我们可以得到所有多项式的表格。表1列出了时的所有多项式,以及作为一个衡量标准。
表 1
| 2 | 4 | |
| 3 | 8 | |
| 4 | 12 | |
| 5 | 18 | |
| 6 | 24 | |
| 7 | 32 |
结论
在上述处理过程中,我们给出了偶次最优多项式的表达式;然而,这些网络函数的极值并未以解析形式确定。在综合步骤中,确定极值所需的数值计算是冗繁的,因此,找到这个问题的答案十分重要。
附录
要确定多项式在(3)和(4)中的形式,我们需要解决以下问题。考虑偶次多项式,它的次数,满足
在这里需要确定多项式,其斜率
最大。有
我们得到
由于非负,其在区间内的所有根都是重根。因此,可以将其写成如下形式
其中是一个没有内部根的奇次多项式,
如果不是线性形式,那么它的次数至少是三。然而,可以证明这是不可能的。因此,应为线性形式,而且从(17)很明显,中的常数项是正的,可以被认为是1。然后,
其中
由于会导致,所以可以排除。如果,我们可以选择足够小的,使得
同时
我们得到
多项式的导数
在点处的值将由下式给出:
这是不可能的。因此,或
因此
为了确定多项式的次数,我们首先将其展开成第一类Legendre多项式的级数,
现在,(13)和(14)变为
和
形成一个函数,满足
然后我们的问题就是确定满足以下等式的(译注:这里使用了拉格朗日乘数法[method of Lagrange multipliers]求约束条件下的极值问题)。
因此,
其中
和
在上述的计算中,我们使用了Legendre多项式的正交关系
和递归公式,
式(31)的解如下所示:
情况
情况
然后,由于(33)中的项
为0,我们得到
因此,
常数可以从(28)方便地求出,
可以通过一个变换从得到(译注:这里是一个简单的线性变换,可以理解为一个线性函数, ,那么即可求出)
由此可以很容易地得到(6)到。
致谢
作者想要表达对Papoulis教授的感谢,因为他关于滤波器的文章,本工作基本上是依据他的方法进行开发的。
参考文献
Manuscript received by the PGCT, December 8, 1958 .
Yokogawa Elec. Works, Ltd., Musashinu-shi, Tokyo, Japan.
[1]: A. Papoulis, “On monotonic response filters,” Proc. IRE, vol 47, pp. 332-333; February, 1959.
[2]: A. Papoulis, “Optimum filters with monotonic response,” P_(ROC). IRE, vol. 46, pp. 606-609; March, 1958[具有单调响应的最优滤波器 ].
[3]: A. Papoulis, “A new class of filters,” 1958 N_(ATIONAL) IRE C_(ONVENTION) R_(ECORD), pt. 2, pp. 42-47.
[4]: E. Jahnke and F. Emde, “Tables of Functions,” B. G. Teubner, Leipzig and Berlin, Germany, pp. 173-183; 1933.
[5]: E. A. Guillemin, “Synthesis of Passive Networks,” John Wiley and Sons, Inc., New York, N. Y., pp. 445-455; 1957.
编辑:黄飞
- 相关推荐
- 热点推荐
- 滤波器
-
滤波器的阶数由什么决定2024-08-15 3773
-
二阶滤波器和一阶滤波器有何特点?两者有什么不同呢?2024-02-05 10649
-
切比雪夫滤波器阶数影响什么2023-12-08 2591
-
一阶低通滤波器的截止频率2023-12-01 8533
-
在连续时间域中比较Papoulis滤波器和Chebyshev滤波器2023-06-10 2715
-
一阶高通滤波器学习2023-01-29 8427
-
二阶有源滤波器的典型结构2022-11-15 2269
-
滤波器的阶数如何确定2020-08-24 54903
-
一文看懂二阶lc低通滤波器的设计及原理2018-04-20 230172
-
滤波器的阶数与衰减陡度2018-02-05 17290
-
二阶有源低通滤波器_最简单的二阶低通滤波器电路图2017-07-24 233927
-
二阶有源滤波器的传输函数2010-05-23 20609
-
三阶不对称滤波器电路2009-12-07 2085
全部0条评论

快来发表一下你的评论吧 !

