

具有单调响应的最优滤波器
EMC/EMI设计
描述
这是翻译自最佳L(Optimum L)或勒让德(Legendre或Legendre–Papoulis)滤波器的提出者发表的《具有单调响应的最优滤波器》的文章,这种滤波器同时具有巴特沃斯的单调频响还有可以和切比雪夫滤波器相媲美的截止特性。
具有单调响应的最优滤波器(Optimum Filters with Monotonic Response)*
A. PAPOULIS , SENIOR MEMBER, IRE
摘要
设计了一类幅频特性在通带无纹波、阻带衰减率高的滤波器;因此它结合了巴特沃斯和切比雪夫响应的理想特征。在给定阶数的所有滤波器中,这个新类型的滤波器在单调递减响应的条件下具有最大截止斜率(cutoff rate)特性。
滤波器的幅频特性可以写成以下形式
其中是的正有理函数;如果网络函数没有有限零点,则是一个多项式,由此产生的滤波器很容易通过一端或两端接载的梯形网络实现。文献中讨论了两类这样的滤波器:巴特沃斯类由:
和切比雪夫类由:
其中是切比雪夫余弦多项式。如果对的唯一要求是对通带中的给定变化具有最大可能的衰减,则滤波器是最佳选择。但是,在许多应用中;即,当同时考虑瞬态响应时,通带中的纹波是不能容忍的;然后使用截止特性不太好的滤波器作为简单的折衷方案。因此,很自然地会探索具有滤波器所需特性且截止速率更快的滤波器。在本文中,我们将确定类型滤波器,其幅频特性随单调下降并且具有最大可能的截止斜率特性。
用表示生成滤波器的多项式,我们有
如果我们进一步假设
我们的问题是在所有阶正多项式中找到满足式(4)和式(5)的正多项式,其斜率
在处是最大的;讨论将仅限于是奇数
在附录中显示多项式由下式给出
其中
是表中所列出的第一类勒让德多项式。点处的斜率由下式给出
由于
我们可以很容易地从式(7)-(9)得到
和
多项式和绘制在图1中和多项式和用于比较;在图2中,显示了相应的幅频特性。
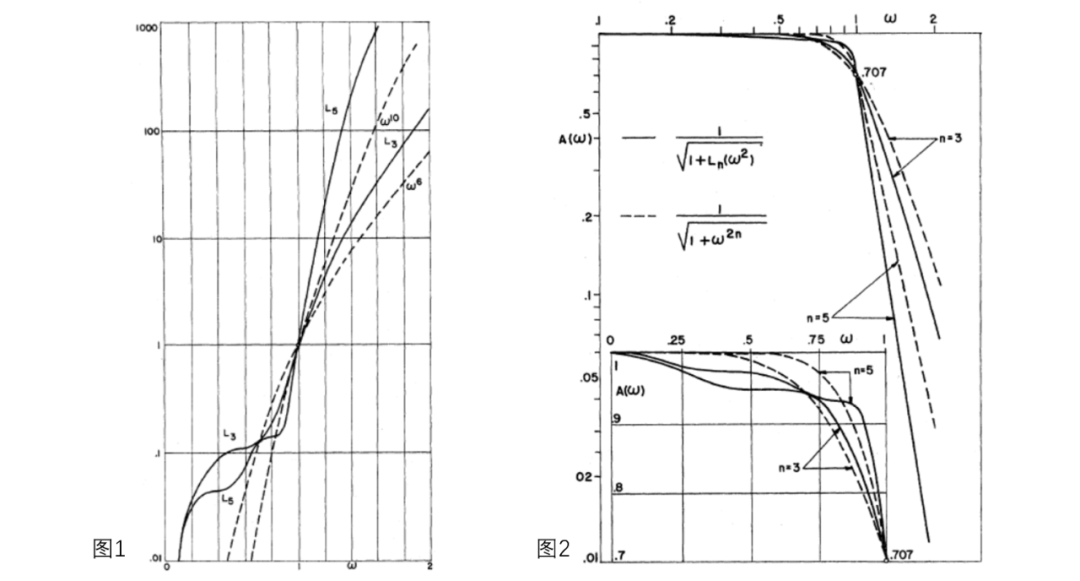
图1 图2
接下来,我们将实现和的滤波器。
: 为了确定振幅等于的网络函数,我们有
然后
因此,
因式分解并保留我们所获得的左半平面的极点
其极点由
并且如图3所示。
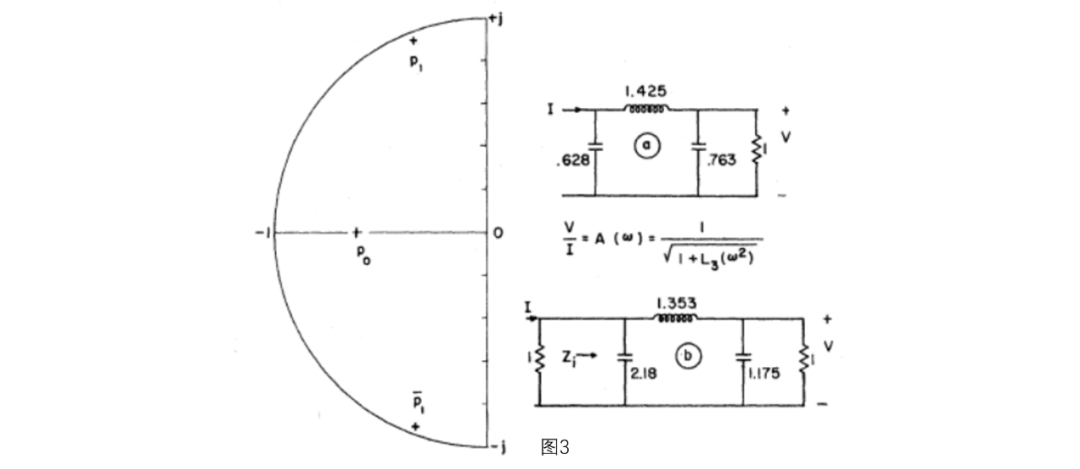
图3
如果可以从的二次因子中获得,而无需对其根进行实际评估可能会很具吸引力;这是有用的,因为在通常的复数根的数值评估方法中,首先会找到二次因子。的确,如果
是
的胡维茨因子(Hurwitz factor),那么很容易看出
要将实现为一个梯形网络,其终端为1欧姆的电阻(见图3)
因此,
将展开为连续分数,我们得到图3(a)所示的网络。要将实现为两端具有1欧姆电阻的梯形网络,我们首先确定由下式定义的反射系数
其中如图3所示。可以看出
因此,
从中我们获得保留了胡维茨因子的
知道了我们可以从
确定,这样,
现在可以实现为一个终止于电阻的无源网络;然而,由于没有有限零点,的实部也是如此,因此,可以展开为连分式,并且如图3(b)所示的网络。
: 我们有
于是,
它的极点由下式给出
从我们得到
从的连分数展开得到图4的网络。
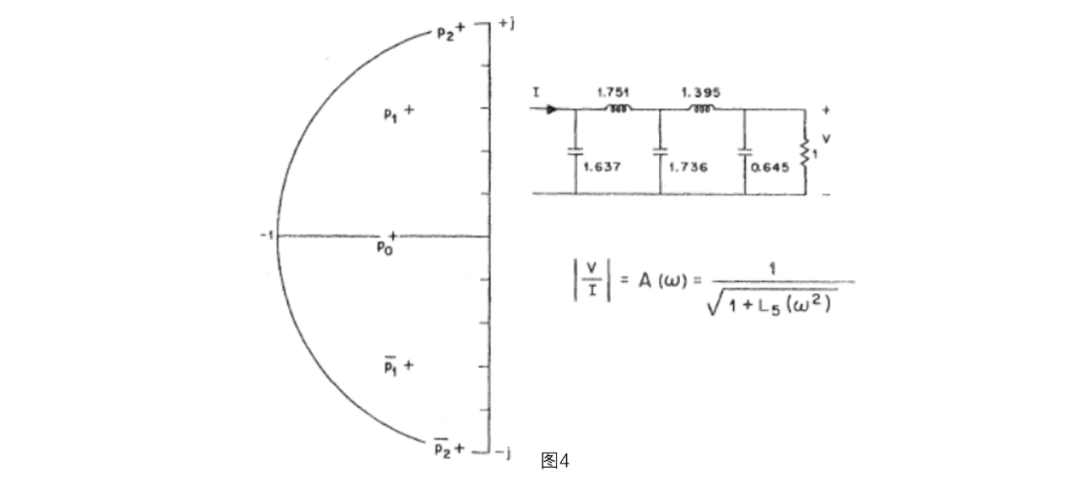
图4
最后,我们将列出、和多项式的重要性质。
多项式: 最大平坦、单调、截止斜率等于。
多项式: 通带中等波纹,在所有多项式的类类型中,它们具有由所给出的最大截止斜率。
多项式: 单调的,在所有单调多项式的类别中,它们具有由所给出的最大截止斜率。
附录
为了证明式(7)-(10),我们首先要解决以下问题。考虑的多项式类使得
在中确定一个多项式使得
最大。
对于
我们有
我们将首先证明阶数为的多项式是一个完全平方;很明显,因为是非负的,它在区间中的所有根都是重的,因此它可以写成以下形式
其中是没有内部根的偶次多项式,这样
在处,可能等于零;在这种情况下
如果不是常数,那么它的次数至少为2,因此,多项式
将与具有相同的阶数,并且对于足够小的,它将保持正值;如果,这是显而易见的[见式(15)],如果,则可以很容易地建立[见式(16)]。因此,如果选择常量
然后,
和多项式
将在中,其在点的导数将由下式给出
这是不可能的[见式(17)],因为被假定为最大值。因此是一个可以取为1的常数。因此
和
为了确定阶数为的多项式,我们首先将其勒让德多项式级数展开
这些多项式满足
从式(18)和式(20)我们得到
由于,并且从式(19)-(21)
如下,我们的问题是确定常数以便在约束式(23)下最大化式(22);这可以很容易地完成,结果由
常数可以很容易地从式(22)和式(24)中求出
可以很容易地通过区间变换从中获得
它在处的斜率由下式给出
其中,式(7)到式(10)很容易得到;这里假设不是限制性的。
脚注
IRE于1957年8月29日收到的原稿。
Polytechnic Institute of Brooklyn. Burroughs Corp., Res. Center, Paoli, Pa.
参考
[1]: A. Papoulis, “On the approximation problem in filter design,” 1957 IRE NATIONAL CONVENTION RECORD, pt. 2, pp. 175-185.
[2]: Küpfmüller, “Die Systemtheorie der Electrischen Nachrichtenübertragung,” S. Hirzel, Zürich, Germany; 1949.
[3]: S. Bernstein, “Leçons sur les Propriétés Extrémales et la Meilleure Approximation des Fonctions d’une Variable Réelle,” GauthierVillars, Paris, France; 1926.
[4]: E. Jahnke and F. Emde, “Tables of Functions,” Dover Publications, New York, N. Y.; 1945.
[5]: A. Papoulis, “Frequency transformations in filter design,” IRE Trans., vol. CT-3, pp. 140-144; June, 1956.
[6]: This problem and its proof is a modified version of a theorem proved by Bernstein, loc cit.
[7]: R. Courant and D. Hilbert, “Methoden der Mathematischen Physik-I,” Springer, Berlin, Germany; 1937.
参考文章
[1] Athanasios Papoulis (1958). Optimum Filters with Monotonic Response. Proceedings to the IRE.
编辑:黄飞
- 相关推荐
- 热点推荐
- 滤波器
-
关于高斯滤波器的响应和逼近2023-04-28 5545
-
FTR滤波器_滤波器原理_有限脉冲响应滤波器_明德扬fpga2017-08-02 4169
-
有源滤波器相位响应2019-10-14 1837
-
具有快速响应的有源滤波器2009-04-15 642
-
无源滤波器的类型2018-08-30 18906
-
针对幅度响应设计的有源滤波器的相位响应介绍2019-04-09 6187
-
开关电容滤波器在ADC中有哪些优势2020-12-07 1275
-
有源滤波器中的相位响应2023-01-06 3655
-
偶数阶勒让德滤波器的设计介绍2023-06-11 752
-
最优单调低通滤波器设计2023-06-16 616
-
数字滤波器的频率响应与模拟滤波器的频率响应有何区别2024-02-05 2695
-
什么是低通滤波器?低通滤波器有什么作用?2024-04-08 6864
-
切比雪夫滤波器的设计步骤2024-08-15 3154
-
模拟低通滤波器的设计方法有哪些2024-11-26 2295
-
电源滤波器的响应时间是多少?2025-01-14 922
全部0条评论

快来发表一下你的评论吧 !

