过拟合、泛化和偏差-方差权衡

机器学习是一个复杂的领域，其最大的挑战之一是构建可以预测新数据结果的模型。构建一个完全拟合训练数据的模型很容易，但真正的考验是它是否可以准确预测新数据的结果。

本文深入探讨了过拟合和泛化的概念，并探讨了它们与偏差与方差权衡的关系。我们还将讨论避免过度拟合和在模型中找到偏差和方差之间最佳平衡的技术。

过拟合

在机器学习中，过度拟合是当模型变得过于复杂并开始过于接近训练数据时发生的常见问题。这意味着该模型可能无法很好地推广到新的、看不见的数据，因为它基本上记住了训练数据，而不是真正学习底层模式或关系。用技术术语来说，考虑一个回归模型，它需要线性关系，而是使用多项式表示。

当模型太擅长从训练数据中学习，但不擅长泛化到新数据时，就会发生过度拟合。这可能是深度学习模型的一个特殊问题，深度学习模型有许多参数可以调整以适应训练数据。

欠拟合

欠拟合与机器学习中的过拟合相反。在欠拟合的情况下（见下图最左边的图表），我们基本上指的是模型对于手头的任务来说太简单的情况。换句话说，模型没有必要的复杂性来捕获数据中的基础模式。在技术术语中，考虑一个回归模型，它需要一个多项式方程，而是使用线性关系表示。

考虑欠拟合的另一种方法是考虑预测房价的例子。如果我们要创建一个仅考虑房屋大小而忽略其他重要因素（如卧室数量）的模型，那么该模型可能会欠拟合数据。发生这种情况是因为模型没有考虑所有相关信息，因此无法准确预测房价。

欠拟合模型往往具有高偏差和低方差，这意味着它在训练和测试数据中都会犯很多错误。这是因为模型无法捕获数据之间的关系，因此无法做出准确的预测。

金发姑娘区和最佳模型复杂性

最佳模型复杂性是机器学习模型既不太简单也不太复杂，但恰到好处地适合它正在处理的数据的最佳点。如果模型过于简单，它可能无法捕获数据中的所有重要模式和关系，并可能导致欠拟合。另一方面，如果模型太复杂，它可能会开始记住训练数据，而不是学习底层模式，这可能导致过度拟合。

找到最佳模型复杂性的目标是在模型拟合和模型复杂性之间取得平衡，其中模型足够简单，可以很好地推广到新数据，但又足够复杂，可以捕获训练数据中的重要模式。

在本文的其余部分，我们将重点介绍可用于找到最佳模型复杂性的不同技术，例如从简单模型开始并逐渐增加其复杂叉验证以评估不同数据子集上的模型，以及使用正则化技术来防止过度拟合。

但首先，让我们首先解释机器学习中两个非常重要的概念，即偏差和方差。

机器学习中的偏差和方差之间的差异

想象一下，尝试创建一个模型来根据房屋的大小预测房屋的价格。我们有一个包含 100 间房屋及其相应价格和大小的数据集。为了进行预测，我们决定使用仅考虑房屋大小的线性回归模型。

现在，创建模型时可能会出现两个问题：偏差和方差。当模型过于简单且无法准确捕获数据中的模式时，就会发生偏差。在这种情况下，如果我们使用只有一个特征（大小）的线性模型，该模型可能无法准确预测房屋的价格，从而导致高偏差。

另一方面，当模型过于复杂并且过度拟合数据时，就会发生方差，这意味着它与训练数据拟合得太近，但在新的、看不见的数据上表现不佳。在这种情况下，如果我们要使用具有许多特征（例如大小平方、大小立方等）的高阶多项式模型，它可能会过度拟合数据，从而导致高方差。

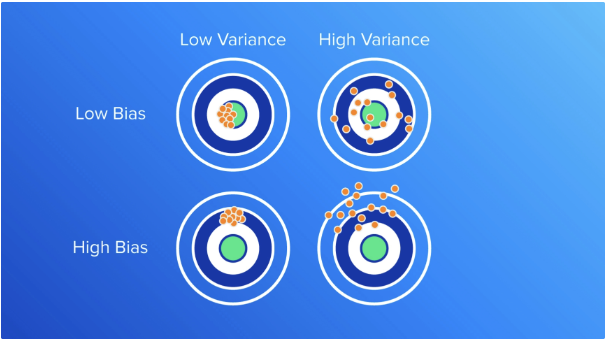
如上图所示，高方差往往会分散模型的输出，因为模型过于复杂并且与训练数据拟合得太近。从本质上讲，该模型捕获了训练数据中的噪声，而不是基础模式。

而在高偏差的情况下，模型倾向于为几乎所有输入值产生相似的输出，这与输入和输出之间的真实关系相去甚远。最佳模型复杂性在于这两个错误之间的平衡，正如我们将在权衡部分看到的那样，模型具有足够的灵活性来捕获数据中的基础模式，但又不会过度拟合训练数据的噪声或特性。

什么是偏差-方差权衡？

偏差-方差权衡是指在偏差和方差之间建立可以很好地推广到新数据的模型所需的平衡。过于简单的模型将具有高偏差但低方差，而过于复杂的模型将具有低偏差但高方差。目标是找到适当的复杂程度，以最小化偏差和方差，从而生成一个可以准确地泛化到新数据的模型。

为了在偏差和方差之间取得平衡，我们希望找到模型复杂度的最佳水平，使其能够准确预测房屋价格，同时很好地推广到新数据。这可以通过创建误差与模型复杂性图来完成，该图显示了模型在不同复杂度级别的性能。通过分析此图，我们可以确定模型复杂度的最佳水平，其中偏差和方差权衡是平衡的。

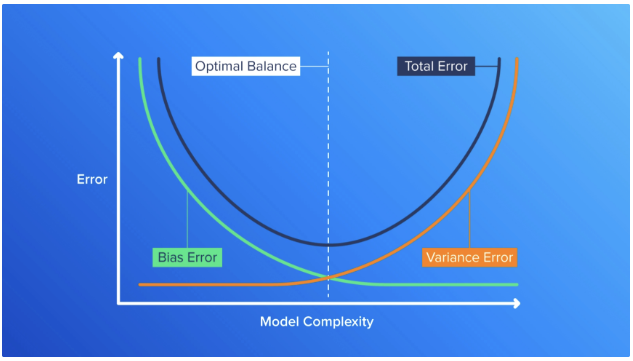
绘制误差与模型复杂性的图形首先要构建一系列具有不同复杂程度的模型。例如，如果我们要创建一个线性回归模型，我们可以从一个只有一个特征的简单模型开始，然后逐渐包含更多特征以使模型更加复杂。

然后，我们将在部分数据上训练每个模型，并在单独的测试集上评估其性能。为了测量测试集上的预测误差，我们可以使用均方误差（MSE）或平均绝对误差（MAE）等指标。

训练和评估每个模型后，我们可以根据模型复杂性绘制测试误差。生成的图形通常显示 U 形曲线，其中误差随着模型复杂性的增加而减小，从而减少了偏差。但是，随着模型变得过于复杂并开始过度拟合数据，误差最终会再次开始增加，从而增加方差。

要确定偏差和方差的最佳复杂度，请在图形上查找检验误差最低的点（如图形中间的虚线所示）。这一点表示此特定问题的偏差和方差之间的最佳平衡。

了解机器学习中的泛化

泛化是模型在新数据上表现良好的能力。泛化良好的模型能够对新数据做出准确的预测，如果我们想在现实世界中使用该模型，这一点很重要。另一方面，泛化效果不佳的模型在训练的数据上可能表现良好，但可能无法对新数据做出准确的预测。这是一个问题，因为这意味着该模型在实践中可能没有用。

当我们训练机器学习模型时，我们希望它不仅能够对我们用来训练它的数据做出准确的预测，而且能够对它以前从未见过的新数据做出准确的预测。这是因为，在现实世界中，我们并不总是可以访问用于训练模型的完全相同的数据，而是新的首次看到的数据点。因此，训练模型不仅要很好地拟合训练数据，而且要很好地泛化到新数据，这一点很重要。

解决过度拟合的正则化技术

各种正则化技术通过在损失函数中添加惩罚项来帮助防止过度拟合，这会阻止模型变得过于复杂。

常用的正则化有两种类型：L1（套索）和 L2（脊）正则化。

套索回归（L1 正则化）

虽然所有三种方法都为损失函数增加了一个惩罚项，但在套索回归的情况下，正则化方法向损失函数添加一个与模型参数的绝对（模块）值成比例的惩罚项。

这种方法鼓励模型对不重要的特征给予较少的权重，因为它具有将某些参数驱动为零的效果，这有助于特征选择。这意味着它可以帮助确定哪些特征是最重要的，并丢弃其余特征。这在处理高维数据集时非常有用，其中有许多功能可供选择。

套索回归在自变量数远大于样本数的高维数据集中特别有用。在这些情况下，套索回归可以帮助识别最重要的变量并减少噪声的影响。

套索回归在自变量数远大于样本数的高维数据集中特别有用。在这些情况下，套索回归可以帮助识别最重要的变量并减少噪声的影响。

岭回归（L2 正则化）

岭回归是另一种类型的线性回归，可用于处理机器学习模型中的过拟合。它类似于套索回归，因为它在损失函数中添加了一个惩罚项（正则化项），但它不是像套索回归那样使用系数的绝对值，而是使用系数的平方。

这具有将不太重要的变量的系数缩小到零的效果，但与套索回归不同，岭回归不会将它们精确设置为零。这意味着岭回归不能像套索回归那样执行特征选择，但它更适合所有特征在某种程度上都很重要的情况。

岭回归在处理具有高度共线性（特征之间的相关性）的数据集时特别有用。在这种情况下，模型可能无法确定哪些特征重要，哪些特征不重要，从而导致过度拟合。通过在损失函数中添加惩罚项，岭回归可以帮助减少过度拟合并使模型更加准确。

弹性网络回归

弹性网络回归通过使用岭回归和套索回归的技术，结合了两全其美的优势。通过将岭回归和套索回归惩罚项添加到损失函数中，弹性净回归可以同时执行特征选择和特征收缩，这使得它比单独使用任何一种技术都更加灵活和强大。

L1 正则化项尝试将模型中的某些系数设置为零，这对于特征选择很有用。这意味着它可以识别有助于预测目标变量并排除不太重要的特征的最重要特征。

另一方面，L2 正则化项有助于控制模型中系数的大小。这对于特征收缩很有用，这意味着它可以减少不太重要的特征对模型性能的影响。

弹性网络回归在处理具有大量特征和高度多重共线性的数据集时特别有用，在这些数据集中，模型可能难以区分重要和不重要的特征。通过识别和缩小不太重要的特征，弹性净回归可以帮助减少过度拟合并提高模型的泛化性能。

解决过度拟合的交叉验证技术

交叉验证

是一种技术，可用于通过评估机器学习模型在有限数据量上的性能来解决过度拟合问题。基本思想是将数据拆分为训练集和测试集，然后在训练集上拟合模型并在测试集上评估其性能。

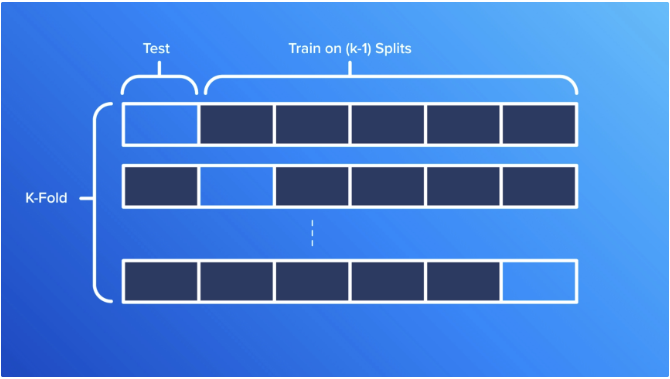
K 折叠交叉验证

一种流行的交叉验证技术是 k 折交叉验证，其中数据被分成 k 个大小相等的部分。模型在零件的 k-1 上训练，并在其余部分进行测试。此过程重复 k 次，每个部分用于测试一次，并且性能在所有迭代中平均。

留一交叉验证

留一交叉验证是另一种技术，其中将单个数据点作为测试集省略，并在剩余数据点上训练模型。请注意，留一交叉验证是 k 折叠交叉验证的特例，其中 k 等于数据集中的数据点数。对于每次迭代，将省略单个数据点作为测试集，并在其余数据点上训练模型。对每个数据点重复此过程，并计算平均性能。

如何选择合适的模型复杂性

为机器学习模型选择正确的复杂性对其性能至关重要。过于简单的模型将无法捕获数据的复杂性并且拟合不足，而过于复杂的模型将过度拟合数据，并且在新数据上表现不佳。

要选择最佳模型复杂性，请从简单模型开始，逐渐增加复杂性，直到获得满意的结果。将数据拆分为训练集、验证集和测试集，并使用验证集选择最佳模型复杂性。使用交叉验证来评估模型在不同数据子集上的性能。

最后，使用 L1、L2 和弹性网络等正则化技术来防止过度拟合。关键是平衡模型拟合和复杂性，评估性能并防止过度拟合，以便模型可以很好地泛化到新数据。

 

审核编辑：郭婷