在约束条件下优化非线性目标函数的问题

非线性规划是一类在约束条件下优化非线性目标函数的问题。以下是几个常见的非线性规划算法：

1. 罚函数法

罚函数法通过惩罚不满足约束条件的点，将非线性规划问题转化为一个无约束优化问题。具体来说，定义一个罚函数 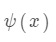，它在可行域内取值为0，否则为一个较大的正数。这样，原问题可以转化为一个带有惩罚项的无约束优化问题，即：

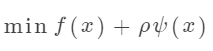
其中， 是一个较大的正数。

2. 信赖域法

信赖域法通过在每次迭代中构建一个局部模型来近似原始问题，然后在局部模型上进行优化。优化完成后，比较原始问题和局部模型的表现，决定是否接受求解结果或者继续迭代。该方法的核心是信赖域半径的精确定义和控制。

3. 内点法

内点法通过引入一个内点路径，使得每个迭代点都在可行域内。具体来说，引入一个惩罚因子 ，并将目标函数 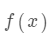中的约束条件 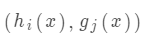替换为一个惩罚项 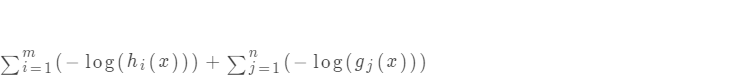。这样，原问题可以转化为一个无约束的优化问题：

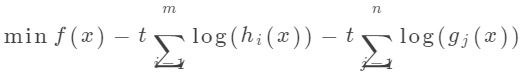
然后，通过一系列迭代，将 缩小至零，从而逐步逼近原始问题。

以上是几个常见的非线性规划算法示例。除此之外，还有很多其他的算法，例如拟牛顿法、次梯度法、粒子群算法等等。

使用罚函数法求解非线性规划的简单示例

在 MATLAB 中，可以使用 fmincon 函数来求解非线性规划问题，其中包括罚函数法。fmincon 函数的使用方法非常灵活，可以通过修改参数来指定不同的算法、约束条件等。

以下是一个使用罚函数法求解非线性规划的简单示例：

假设有以下优化问题：

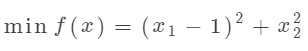
满足以下约束条件：

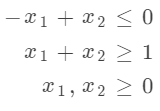
对于罚函数法，我们可以将上面的约束条件转化为惩罚项，即：

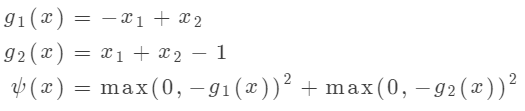
然后将目标函数和罚函数相加，得到无约束优化问题：

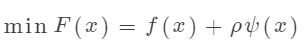
其中 是一个较大的正数。

下面是 MATLAB 的代码实现：

 

% 定义目标函数和约束条件
f = @(x) (x(1)-1)^2 + x(2)^2;
g = @(x) [x(2)-x(1); x(1)+x(2)-1];

% 定义罚函数
rho = 10;
penalty = @(x) max(0,-g(x))^2;

% 定义总目标函数
F = @(x) f(x) + rho * penalty(x);

% 定义初始点和约束条件
x0 = [0; 0];
A = [-1 1; 1 1];
b = [0; 1];

% 调用fmincon函数进行优化
options = optimoptions('fmincon','Display','iter');
[x,fval,eflag,output] = fmincon(F,x0,A,b,[],[],[],[],[],options);

 

在上面的代码中，首先定义了目标函数 f 和约束条件 g，然后通过罚函数法将其转化为无约束优化问题。最后，调用 fmincon 函数来求解优化问题。

需要注意的是，使用罚函数法求解非线性规划问题时，要根据实际情况选择合适的惩罚系数 。过小的 可能导致解不准确，过大的 可能导致数值不稳定。

　　审核编辑：汤梓红