基于平面投影的单目视觉AGV定位算法

 

     

0 引言

 视觉定位是计算机视觉中的一个重要研究问题，广泛应用于机器人自主导航、机器人定位、视觉伺服、摄像机校正、目标跟踪、视觉检测、物品识别和工业零部件装配等领域。近年来，计算机视觉飞速发展，涌现出大量的技术与算法，如主动视觉、面向任务的视觉、基于知识的视觉、基于模型的视觉以及多传感器和集成视觉等方法[1]。根据使用镜头数目分类，计算机视觉分为单目视觉定位、双目视觉定位与多目视觉定位。双目立体视觉是基于视差原理，由多幅图像获取物体三维几何信息。相比于基于多相机的模型定位方法，单目视觉的优点主要体现在只需单幅图像技能实现定位，不存在图像匹配问题，处理速度快，定位精度高。  传统视觉对目标定位，是通过对摄像机的内外参数进行标定来实现的[2]。计算机标定方法可以分为传统标定方法、自标定方法和基于主动视觉的标定方法[3]。传统标定方法是现在使用最为普遍的标定方法，利用结构已知、高加工精度的标定块作为标定物，用摄像机拍摄若干幅标定物的图片，通过计算2D 图像点与3D 空间点之间的关系来完成标定，通过对标定物的合理设计得到高精度的结果。该方法的优点是适用各种摄像机模型，定位精度高，缺点是标定过程复杂。自标定方法不需要标定物，仅通过运动摄像机所拍摄的标定图片中匹配点的关系来进行标定。由于不需要标定物，该方法适用范围广、灵活性强，但是图像匹配中需要求解多元非线性方程导致其鲁棒性较差[4]。基于主动视觉的标定方法需要预知摄像机的详细运动信息，这需要昂贵的设备对摄像机的运动轨迹进行记录，实验成本较高[5]。  本文针对AGV 所处的平坦路面的单目视觉定位，提出了一种新的简单可行的算法。该算法不需要对摄像机进行标定，也不需要求解摄像机的内、外参数，通过分析图像像素平面与现实空间平面的几何关系，得出像素点与现实点间的映射关系。实验结果表明 , 文中提出的算法定位精度高 , 实时性好 , 为解决计算机视觉的测量、定位与AGV 视觉导引提供一种新的思路，具有进一步研究的价值。  

1 摄像机模型及存在的问题

 1.1 摄像机模型本文采用理想的针孔摄像机模型[6]，忽略实际摄像机中的畸变问题。针孔成像模型又称为线性摄像机模型，空间中任何一点在图像中的成像位置可以用针孔成像模型近似表示，即任何一点在图像中的投影位置p 为光心O 与P 点的连线OP 与图像平面的交点。分别以其次坐标m=[u,v ,1]T,W=[X,Y,Z ,1]T 来表示像素点p 及空间点P ，根据针孔摄像机成像模型，投影方程为  

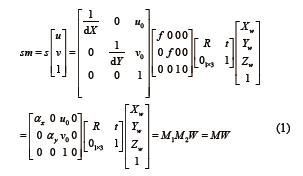
 式中：αx=f/ dX 为u 轴上的尺度因子，或称为u 轴上的归一化焦距；αy=f/ dY 为v 轴上的尺度因子，或称为v 轴上的归一化焦距；M 为3×3 矩阵，称为投影矩阵；M1 由αx、αy、u 0、v 0 决定，由于αx、αy、u 0、v 0 只与摄像机内部参数有关，称这些参数为摄像机内部参数；R、t 分别表示摄像机坐标系与世界坐标系之间旋转矩阵和平移向量，M2 称为摄像机外部参数。确定某一摄像机的内外参数，称为摄像机标定。  1.2 存在的问题在单目视觉方法测量物体位姿时，如果物体上的某些特征在物体坐标系下的坐标已知，要求出这些特征在摄像机坐标系下的三维坐标，进而求出摄像机坐标与物体坐标系之间的相对位姿关系。在这个问题中，一般需要求得摄像机内外参数进行投影计算。如果摄像机固定，摄像机外参数一般固定不变，而摄像机内参数只与摄像机硬件有关，定焦摄像头的内参数固定不变。如果已知摄像机内外参数，就已知投影矩阵，这时对任意空间点，如已知它的坐标，就可以求出它的图像点的位置。反过来，如果已知某空间点的图像点的位置, 即使已知摄像机的内外参数，也不能唯一确定。这是因为，已知图像点时，由针孔成像模型，任何位于射线上的空间点的图像点都是点。因此，该空间点是不能唯一确定的。为解决这一问题，单目视觉在特定环境内设置一个人工图标，图标的尺寸以及在世界坐标系中的方向、位置等参数都是已知的；而双目视觉通过不同视角拍摄两幅或多幅图像，增加约束条件[7]。本文提出一种新的单目视觉投影定位算法，在该算法中，现实平面中的二维空间点先投影到一个虚拟参考平面上，如图1 所示，该参考平面与摄像机光轴垂直且与成像平面平行，然后虚拟参考平面上的点通过镜头平行透视写入成像平面，并形成图像像素点。在第二步平行透视中，参考平面与成像平面只是简单的缩放关系，保留了透视成像中丢失了的平行属性与位置属性。这样，所述问题就转化为虚拟参考平面与现实平面之间的映射求解问题。    

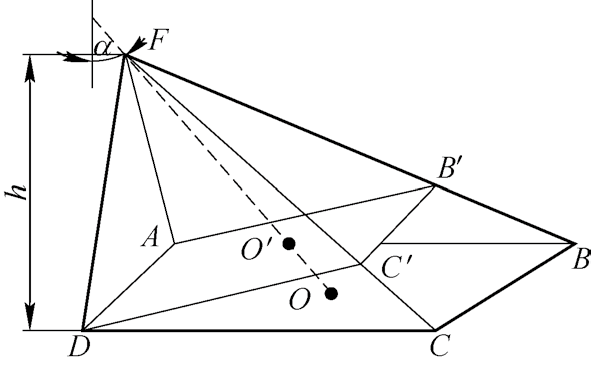
   图1 摄像机、参考平面、现实平面示意图    

2 图像像素平面与现实平面的映射关系

 首先约定摄像机、参考平面、现实平面的坐标系，如图2~ 图4 所示。    

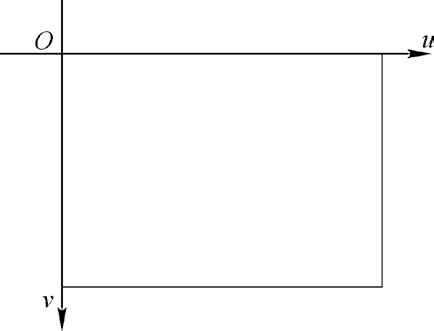
 图2 像素坐标系    

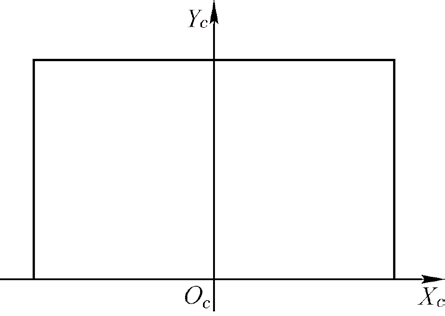
   图3 参考平面坐标系    

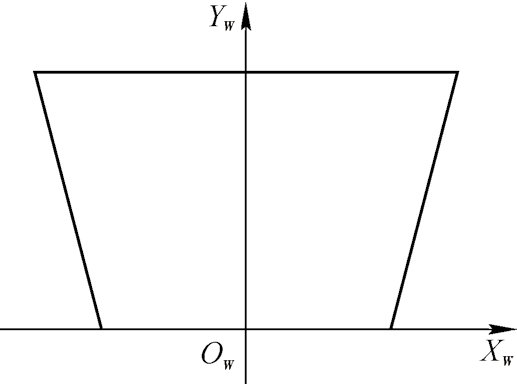
     图4 现实平面坐标系  2.1 像素平面到参考平面由于摄像机垂直于参考平面 , 所以像素平面到参考平面是等比例缩放的，它们之间只相差一个比例系数。由于参考平面AD 边与现实平面AD 边重合，可以通过实际测量得到AD 边的实际长度。参考平面与像素平面等比例缩放，由图像像素长宽比可求得AB' 长度。若W=|AD |，L =|AB' |，图像像素分辨率为m×n ，可得对应像素平面上一点p (u ，v ) 的参考平面坐标为P (Xc ,Yc )，有  

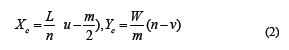
   2.2 参考平面到现实平面虚拟参考平面与现实平面在模型中是简单的平面投影关系，只要求解出平面投影的单应性矩阵，就能得到它们之间的映射关系。平面投影定理[8]：对于一个平面投影，一定存在一个非奇异3×3 矩阵H，使得对任何P 2 上的齐次点x ，有h (x )=Hx 。    

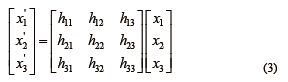
   或简记为x' =Hx 。其中H 称为单应性矩阵，这个投影变换有8 个自由度。将参考平面坐标（Xc，Yc），现实平面坐标（Xw，Yw）用齐次坐标表示为（Xc，Yc，1），（Xw，Yw，1）。则参考平面与现实平面间投影关系为    

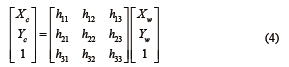
   由于现实空间点在同一平面，设h 33=1, 每一组对应点可得：    

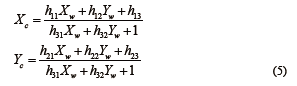
   由四组对应点就可以得到8 个关于H 的元素的线性方程组    

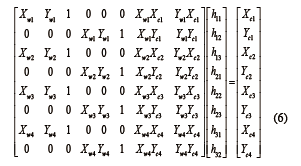
   用AH=B 来表示上式，则H=A-1B 。检测到图像上特征点的像素坐标值，通过式（2）、式（4）可得该特征点在现实平面对应点的坐标，由此可以达到单目视觉定位的目标。  

3 AGV 定位实验与结果分析

 为了验证本文算法的精度，设计了AGV 定位实验。采用MV-U300 工业相机，6~12 mm 变焦镜头，拍摄室内地面。为了验证该算法的精度，在地面上放置一张4×4 的黑白棋盘图。棋盘长宽200 mm，每小格边长50mm，如图5 所示。测得相机视野四个顶点坐标分别为A（-235, 0），B（-575，960），C（575,960），D（235,0）；由相机参数计算得到的参考平面的四个角点坐标为A' (-235,0)，B' (-235,352.5)，C' (235,352.5)，D' (235,0)；计算投影变换的单应性矩阵，有    

     

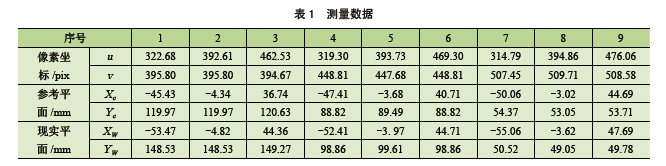
   图5 原始图像（左）与变换图像（右）  为检验本文算法的定位精度，对所采集图像进行Hough 变换检测直线，从而获取图中所示棋盘图黑白色块的9 个交点像素坐标( 自左至右、从上往下排)，通过本文算法求得对应的参考平面交点，再通过单应性矩阵求得对应点的现实平面坐标。具体实验数据见表1。通过现实平面的实际坐标计算黑白色块的边长，与真实值50 mm 比较，可以发现横排误差在±3% 以内，竖排误差在±5% 以内；竖排误差比横排误差大，主要是因为图像竖向放大系数相对变化较大。结果表明，该方法测量精度较高，可以满足一般的定位系统要求。    

     

4 结论

 本文提出的算法结合单目视觉导引AGV 小车，省去了传统视觉定位方法中的摄像机标定环节，采用平面投影的思路解决单目视觉定位，简化了视觉导引AGV小车导引模块的硬件配置与定位计算。该算法针对通用摄像机模型针孔相机模型，利用平面投影原理，对平坦路面实现了单目视觉定位。实验结果表明，该方法简单可行，对室内AGV 和室外平坦路面AGV 的路径导航与视觉避障都有一定的实用价值，为解决机器视觉的定位、测量问题提供了一种新思路。