

FPGA有符号数,定点小数表示及计算机数值表示规则
可编程逻辑
描述
计算机体系中,计算机并不认识负数,那么计算机是如何表示负数呢?
当计算机需要考虑负数时,我们常称有符号数表示;反之则为无符号数表示。
有无符号数代表了当前运算过程是否存在负数,这个符号数的意义是什么,需要从1+1=(1)0讲起。
以C语言的char类型为例,char字符占用8bit,从0000 0000 到1111 1111 ,正常人都知道1+(-1) = 0,而在8bit的char类型里面,什么数字+1会变成0?
答案是:1111 1111 + 0000 0001 = (1)0000 0000
可以看到1111 1111与0000 0001 相加最后会产生一个进位1和0000 0000,由于8bit的限制,进位溢出,最后的结果就是0000 0000。
所以,在有符号数表示的情况下,-1在计算机的表示方式就是1111 1111,同样,-2对应1111 1110等,最后得出规律,负数的表示方式为其绝对值的补码的表示方式。取补码过程如下:
以-1为例,8bit情况下
- -1的绝对值为1,其对应的8bit表示:0000 0001
- 位取反,得反码,1111 1110
- 反码加一得补码,1111 1111
而正数则做好自身即可,不需做变换;有符号数表示情况下,n bit信号可以表示从
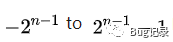
的整数,无符号数表示情况下,n bit信号可以表示从

的整数,注意信号的表示范围,小心运算结果溢出,即运算结果超出上下限导致结果不对;
实际上,有符号情况下,最高位都是符号位,影响数据的正负性;当最高位为1,表示负数;最高位为0,则为非负数,这就是为什么会用有符号数表示当前存在负数情况的意义。
回到BPSK的FPGA工程中,我们需要遵循开头所述的映射规则,
- 0 -> -1
- 1 -> +1
一行代码解决:
wire[1:0] code_o ;assign code_o =(code ==1'b1)?2'b01:2'b11;
因为在FPGA中,数据的位宽可以随意设置,我们设置映射后的数据位宽为2bit,相较于m序列输出的code信号只增加一个符号位,并通过三目运算符完成需要的有符号数表示,符合需要的映射规则。
因为后续与载波相乘可能会涉及到FPGA内部的小数表示,所以这里一并讲到。
FPGA本身无法表示小数,其内部的小数表示都是按照某些协定的规则去理解的。
FPGA表示小数有定点数和浮点数两种方法,从简单的定点数讲起,复杂的浮点数将在下篇文章讲到。
熟知数电的数值规则可知,1.5可以表示为(01.10)的二进制,即:

同理,0.75可以表示为(00.11)的二进制。
虽然FPGA并没有小数点,但我们心中有这个小数点。
两者相加,0110 + 0011 = 1011
在无符号数情况下,在心中加上对应小数点,(10.11)也就是2.25 。
但在有符号情况下,这个结果就不对,超过了4bit有符号2个小数位能表示的上限,这个时候就需要进行符号位扩展,即扩展最高位,将最高位复制多个,放在最高位。
增加一个符号位,00110 + 00011 = 01011,这在有符号情况下就对了。
注意,定点数做加法需要对准小数点,1.5可以用(01.1)表示,但是为了与(00.11)相加,(01.10)尾部需增加一个0,不影响大小却使两个数的小数点对齐,也就是说两个定点小数相加,小数位少的需要在尾部加零,直到两者小数位一样。
乘法规则,为了表示特殊结果,使用1.5(01.10)和-0.75(11.01)相乘。

相乘过程 图1
从图1可以看到相乘过程,前三行比较简单,到第四行时,符号位1乘以0110,这个时候0110需要取补码,并且扩展1位符号位防止溢出,如果符号位为0则第四行直接为0;
可知最终结果为11101110,而(01.10)和(01.10)的小数位都是2位,相乘后为4位,所以最终表示为(1110.1110),根据补码计算,可知结果为-1.125,结果正确。
乘法规则需要注意最高位符号位,适当时可以扩展符号位防止数据溢出,并根据乘数的小数位确定最终的小数位。
小数位的确定根据两个数的小数位数相乘,再自行加在最终结果上。
-
定点数表示实数的方法以及定点数在硬件上的运算验证2025-10-28 118
-
定点小数运算2025-07-25 439
-
请问AFE5801 AD转换后数字信号是用有符号数还是无符号数表示的?2025-02-11 339
-
FPGA定点数截位的基本准则2023-06-19 2271
-
FPGA浮点数表示及计算机数值表示规则2023-06-16 2079
-
计算机组成原理——数值型数据的表示2023-05-25 6909
-
FPGA零基础学习:数字电路中的数字表示2023-02-15 1406
-
请问AFE5801 AD转换后数字信号是用有符号数还是无符号数表示?2019-05-24 3474
-
一文了解FPGA浮点小数与定点小数的换算及应用2018-06-28 8113
-
在FPGA里浮点数与定点数表示法原理展示2017-11-18 9279
-
有符号数,无符号数,浮点数探讨2015-04-29 6009
-
定点小数的表示方法2009-10-13 8683
-
计算机的运算方法2009-04-11 453
全部0条评论

快来发表一下你的评论吧 !

