

FPGA浮点数表示及计算机数值表示规则
可编程逻辑
描述
定点数硬件实现简单,但表示的范围有限,且部分的小数运算IP核只支持浮点数运算,因此这里还需要提到浮点数的相关内容。
通过介绍FPGA浮点数的表示方法和用法,进而讲述计算机浮点数的表示规则,这部分涉及数电,微机原理的基础知识。
浮点数需要提到IEEE754标准,计算机的浮点数表示依照这个标准,以IEEE754的单精度浮点数为例。
IEEE754单精度浮点数为32位,分为符号位,8位的指数部分,23位的尾数部分;
以十进制下的12.5为例,首先12.5非负,所以符号位为0;
12.5转换为二进制,1100.1,将其科学计数法化(正规化),变成了
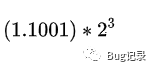
可知道此时2的指数为3,加上预设的偏移值127,得到了130,即1000 0010;这就是指数部分。
(1.1001)去掉整数得到尾数1001,剩余尾数补0,这就是尾数部分。
所以最终的IEEE754单精度值为 0 1000 0010 1001 0000 0000 0000 0000 000
整合为16进制,为41 48 00 00 。
再以-0.375为例,符号位为1;
0.375转换为二进制,0.011,科学计数法化(正规化),

可知2的指数位-2,加上127为125,即0111 1101;
(1.1)去掉整数得到尾数1,剩余尾数补0
最终为1 0111 1101 1000 0000 0000 0000 0000 000
整合为16进制,为BE C0 00 00。
反过来,通过浮点数的16进制表示,推出相应的10进制数,公式如下:
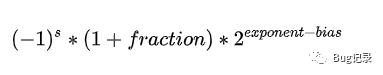
s是符号位,决定数据的正负,fration是最后的23位对应的10进制小数,exponent是8位的指数部分,bias是预设的偏移值,32位中为127;
当然,这样的计算方法没有办法表示0,所以做了特殊规定,当exponent为0时,相应的公式变成了这个样子:

当fration也为0时,就表示出0了。当exponent为最大值,fration为0,表示正/负无穷大;fration不为0会报NaN,不是一个数。
浮点数加法:
以正数相加为例, 0.3 + 0.7 = ?
- 0.3 -> 3E 99 99 99
- 0.7 -> 3F 33 33 33
可以知道,0.3的exponent为125,0.7的exponent为126;两者的exponent不一致,需要进行移位操作保持一致。这里移位的原则是小exponent向大exponent保持一致。所以0.3需要向右移动一位,保持exponent一致;
即(1) 0011 0011 0011 0011 0011 001 -> (0) 1001 1001 1001 1001 1001 100
然后进行两者尾数相加,这部分跟定点数加法规则一致。

得到结果3f 7f ff ff,转换为10进制为0.9999999403953552;也就是说在计算机浮点数操作过程中,0.3+0.7不等于1,这也就是为什么编程里面浮点数不推荐直接做比较的原因,由于浮点数精度的原因,浮点数做比较更推荐使用与预设值做减法取绝对值,如果差值在一个很小的范围内,则认为相等。
如果是正负相加,负数需要取补码进行相加操作,并扩展符号位,观察结果的正负性;如果结果的整数部分大于1,要进行科学计数法化(正规化)。
浮点数乘法:
- 尾数相乘,得到结果,以12.5和-0.375为例,相关的浮点数表示在介绍IEEE754环节已给出;
12.5 ->41 48 00 00 ; -0.375 -> BE C0 00 00

- 计算两者的exponent差值,得到结果1;将1中的结果科学计数法化(正规化),得到最终的exponent为127+1+1=129;
- 将两者的符号位做异或计算,得到结果1,所以最终结果的符号位为1;最终结果为C0 96 00 00,转换为10进制就是-4.6875 。
相对比而言,浮点数能够表示更宽的数据范围,但计算过程可能较为复杂,但是明白它的表示规则之后,将定点小数转换成浮点数也并不难,这样就可以用到浮点运算的IP核了。
经过各种处理之后的数据,为了平衡数据精度和资源占用,又需要使用到数据截位。
-
定点数表示实数的方法以及定点数在硬件上的运算验证2025-10-28 119
-
一文带你秒懂IEEE 754浮点数2024-03-18 12470
-
modbus浮点数怎么读取2023-12-28 9419
-
单精度和双精度浮点数的区别2023-12-13 14117
-
定点数和浮点数的概念 浮点数二进制序列与指数表达式之间的转化2023-08-22 9828
-
FPGA有符号数,定点小数表示及计算机数值表示规则2023-06-16 3208
-
什么是浮点数?浮点数在内存中的存储2022-11-09 7126
-
基于FPGA实现的自定义浮点数2022-10-10 1948
-
浮点数基础知识科普2020-03-08 17062
-
单片机浮点数运算的源码设计2018-03-07 11182
-
在FPGA里浮点数与定点数表示法原理展示2017-11-18 9280
-
第7章 DSP定点数和浮点数2016-09-22 4253
-
浮点数的表示方法2009-10-13 17042
全部0条评论

快来发表一下你的评论吧 !

