MATLAB基础教程(xlsread和xlswrit函数+数据拟合+数值计算)

1、xlsread和xlswrit函数

        在MATLAB中经常会用到数据的读取，首先是从Excel中读取数据到MATLAB中去。下面给出原始Excel数据内容：

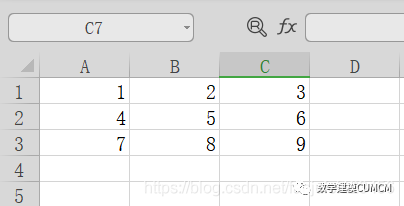
        在MATLAB读取结果如下：

 

m=xlsread('fanjufei.xls',1,'A1:C3')


m =


     1     2     3
     4     5     6
     7     8     9

 

其中xlsread可以直接从Excel中读取文件，'fanjufei.xls'表示读取文件的名称，1表示位于sheet1；'A1：C3'表示读取数据的范围。

xlswrite函数:

        可以从MATLAB中写入数据到Excel中去，下面给出要写入数据：

 

clear
clc
n=[1 2 3 4;5 6 7 8;9 10 11 12];
xlswrite('fanjufei.xls',n,3,'B2:E4')

 

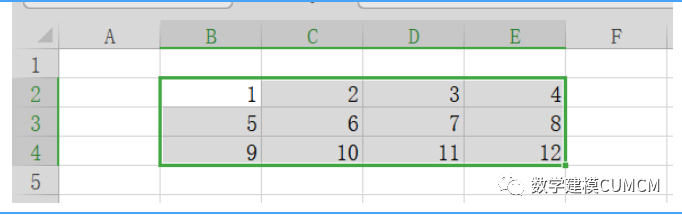
2、数据拟合

2.1 多项式拟合

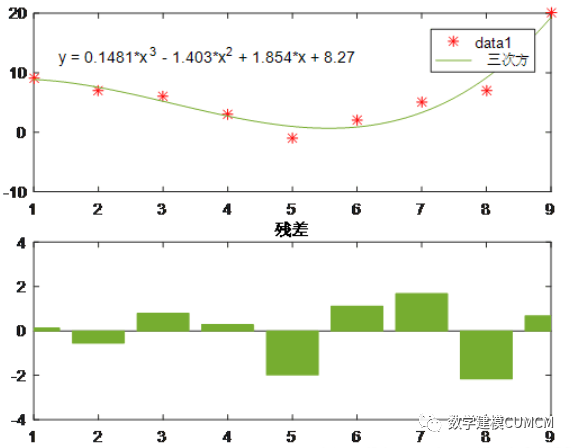
        例如：有两组数据为x=[1 2 3 4 5 6 7 8 9];y=[9 7 6 3 -1 2 5 7 20];写出x与y的表达式；

 

clear
clc
x=[1 2 3 4 5 6 7 8 9];
y=[9 7 6 3 -1 2 5 7 20];
P=polyfit(x,y,3);
xi=010;
yi=polyval(P,xi);
plot(xi,yi,x,y,'r*');

 

注释：polyfit(x,y,N)，x、y为原始数据，N为拟合最高次幂，

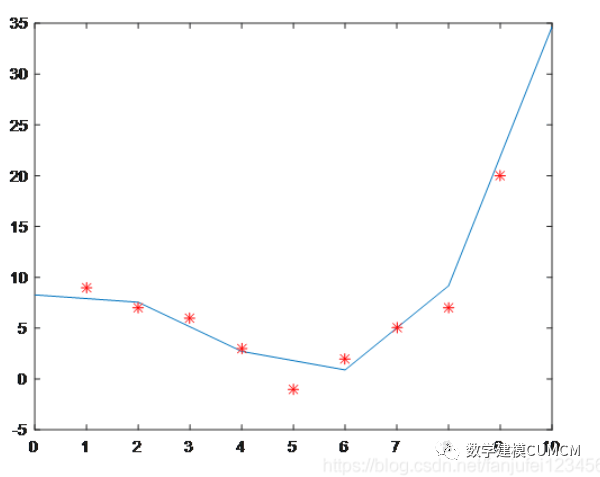
polyval(P,xi)，P为各项的系数，结果展示为：

                                P  0.148 -1.403 1.8536 8.2698

 故多项式的结果为：

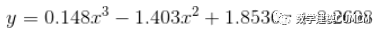
2.2 工具箱拟合

        打开工具→基本拟合，选定拟合的方式。

 

x=[1 2 3 4 5 6 7 8 9];
y=[9 7 6 3 -1 2 5 7 20];
plot(x,y,'r*');

 

得出结果如下：

2.3 自定义拟合函数

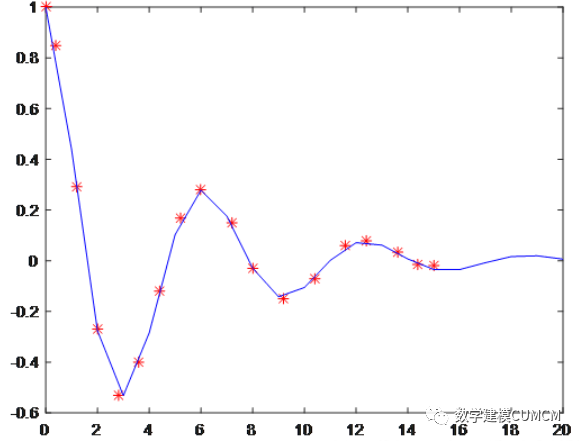
        例如：要拟合数据：

 

clear
clc
syms t
x=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];
f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
cfun=fit(x,y,f)
xi=020;
yi=cfun(xi);
plot(x,y,'r*',xi,yi,'b-');

 

结果：

 

cfun = 


     General model:
     cfun(t) = a*cos(k*t)*exp(w*t)
     Coefficients (with 95% confidence bounds):
       a =      0.9987  (0.9836, 1.014)
       k =      -1.001  (-1.006, -0.9958)
       w =     -0.2066  (-0.2131, -0.2002)

 

        注释：fittype是自定义拟合函数，cfun=fit(x,y,f)拟合数据x、y，x、y必须为列向量。

        故结果为：

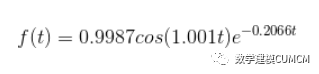
3、数值计算

3.1 多项式

（1）多项式表示方法

（2）多项式的运算

多项式乘除运算

    计算代码：

 

clear 
clc


%多项式相乘conv
u=[2 4 5 6];%多项式
v=[10 20 30];%多项式
p=[1 2 3];%多项式
w=conv(u,v)  %conv为多项式相乘函数，也可以嵌套使用；
m=conv(conv(u,p),v)  


%多项式相除deconv
[q,r]=deconv(w,v) %q为商，r为余数；

 

结果：

 

w =


    20    80   190   280   270   180


m =


 20         120         410         900        1400        1560        1170         540


q =


     2     4     5     6


r =


     0     0     0     0     0     0

 

多项式的导函数

  k=polyder(p),返回多项式p的导函数；
  k=polyder(a,b),返回多项式a乘以b的导函数；

  [q,d]=polyder(b,a),返回多项式b整除a的导函数，其分子返回给q，分母为d；

 

clear
clc
x=[1 2 3 4];
y=[1 2 3 4];
z=polyder(x,y)

z =


     6    20    40    60    50    24

 

多项式求值

     y=polyval(p,x),代数多项式求值，若x为一数值，则求在该点的值；若为向量、矩阵，则求向量、矩阵中的每一个值；
     y=polyvalm(p,x),矩阵多项式求值，要求x为方阵；

 

p=[1,2,3];
x=1:5;
y=polyval(p,x)

y =


     6    11    18    27    38

 

多项式的根

    函数roots：可以求出多项式等于0的根；
    函数poly：可以通过多项式等于0的根，求出多项式；

 

p=[1 2 1];
r=roots(p) %求p的根
v=poly(r)  %求r根的多项式

r =


    -1
    -1


v =


     1     2     1

 

3.2 曲线拟合

        曲线拟合用一个比较简单的函数去逼近一个未知的函数，曲线拟合最优的标准采用最小二乘法原理，拟合的结果使得误差的平方和最小。

        在MATLAB上最常采用polyfit函数来求最小二乘拟合多项式的系数，再用polyval函数求出多项式在所给出点的值；

 

x=linspace(0,2*pi,50);
y=cos(x);
p=polyfit(x,y,6);
t=linspace(0,2*pi,50);
y1=polyval(p,t);
plot(x,y,t,y1,'r*')

 

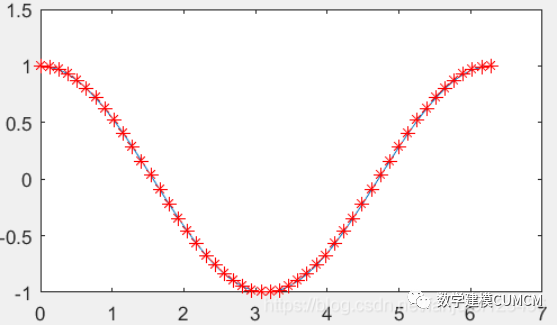
 从图像上可以看出拟合比较好，红色星号都在曲线上；

3.3 数据插值

（1）一维数据插值

        插值函数：yi=interp1(x,y,xi,method)

        根据在x，y处的值，计算函数在xi处的值，其中xi的值不能大于x的值；

        method插值方法：linear（线性插值）、nearest（最近点插值）、cubic（3次多项式插值）、spline（3次样条插值）；

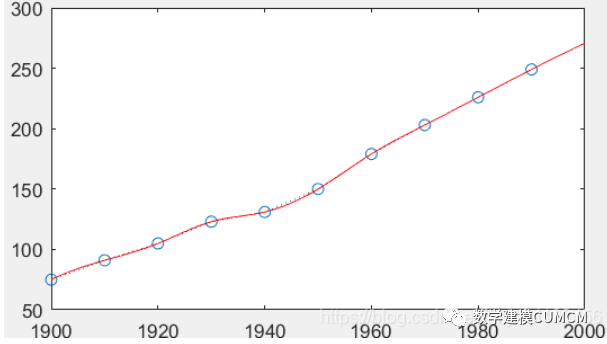
        例2：下面为1900—1990每隔10年的人口普查数据：

                t=19001990;

                p=[75 91 105 123 131 150 179 203 226 249]

求在1985年人口数值；

 

t=19001990;
p=[75 91 105 123 131 150 179 203 226 249];
yi=interp1(t,p,1985)

 

  得出1985年的人口数为： 

 

yi =


  237.5000

 

估计1900—2000年人口数值

 

t=19001990;
p=[75 91 105 123 131 150 179 203 226 249];
xi=1900:2000;
yi=interp1(t,p,xi,'spline');
plot(t,p,':o',xi,yi,'-r')

 

（2）二维数据插值

         插值函数：Z1=interp2(X,Y,Z,XI,YI,method)

         X,Y为原始采样点，Z为对应的采样值，XI,YI表示欲插值的点，method为插值方法与一维插值方法一样；

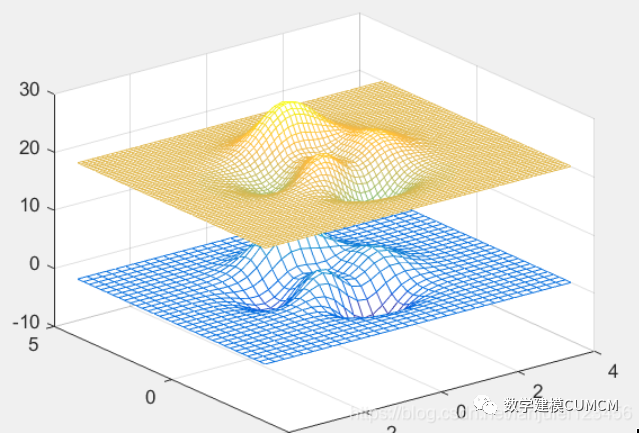
         例3：为函数peaks插入更多的线条；

 

[X,Y]=meshgrid(-44);
Z=peaks(X,Y);
[XI,YI]=meshgrid(-44);
ZI=interp2(X,Y,Z,XI,YI);
mesh(X,Y,Z)
hold on
mesh(XI,YI,ZI+20)

 

3.4 数值微积分

（1）数值微分

        在MATLAB中没有直接求数值导数的函数，只有计算向前差分的函数diff，其调用格式为：

        DX=diff(X)：计算向量X的向前差分，DX(i)=X(i+1)-X(i)，i=1......n-1；

        DX=diff(X,n)：计算X的n价向前差分；

        DX=diff(A,n,dim)：计算矩阵A的n价差分，dim=1（默认值）

 

x=[3 2 1];
dx=diff(x)

dx =


    -1    -1

 

（2）数值积分

  被积函数是解析式

  MATLAB有两种函数求解定积分，调用格式为：

          quad(函数,a,b,tol,trace)

          quadl(函数,a,b,tol,trace)

  其中，a为下限，b为上限，tol为精度，trace是否展现积分过程；

 

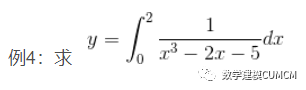
f=inline('1./(x.^3-2*x-5)');
y=quad(f,0,2)
y1=quadl(f,0,2)

y =


   -0.4605
y1 =


   -0.4605

 

被积函数为表格定义

    用trapz(x,y)来进行计算，x为向量，y为x的函数；

 

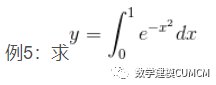
x=01;
y=exp(-x.^2);
trapz(x,y)

ans =


    0.7468

 

二重积分数值求解

  MATLAB提供的函数为：

                                  y=dblquad(f,a,b,c,d,tol,trace)，

 

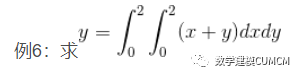
function f= fan(x,y)
f=x+y;
end

y=dblquad('fan',0,2,0,2)

 

  结果：

 

y =


     8

 

3.5 线性方程组求解

（1）直接解法

  对于方程Ax=b来说，可以用x=A；即x=inv(A)*b;

 

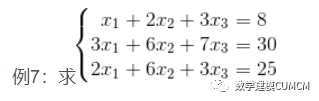
A=[1 2 3;3 6 7;2 6 3];
b=[8 30 25]';
x=A

x =


   17.0000
    0.0000
   -3.0000

 

（2）LU求解、QR求解、Cholesky求解

  例8：求例7；

 

A=[1 2 3;3 6 7;2 6 3];
b=[8 30 25]';
[L,U]=lu(A); %LU分解
x=U(L)


[Q,R]=qr(A); %QR分解
x_val=R(Q)


R=chol(A);   %Cholesky分解
x_val_1=R(R')

 

3.6 常微分方程数值求解

基于龙格—库塔法，MATLAB提供的常微分方程求解的函数为：

          [t,y]=ode23('fname',tspan,y0)，二价、三价龙格—库塔法；

          [t,y]=ode45('fname',tspan,y0)，四价、五价龙格—库塔法；

         fname是定义f(t,y)的函数文件名，该函数文件必须返回一个列向量；tspan形式为[t0,tf]表示求解区间，y0是初始状态列向量；t      给出时间向量，y为状态向量；

 

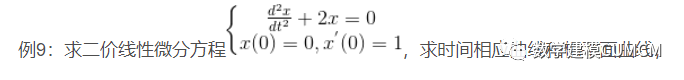
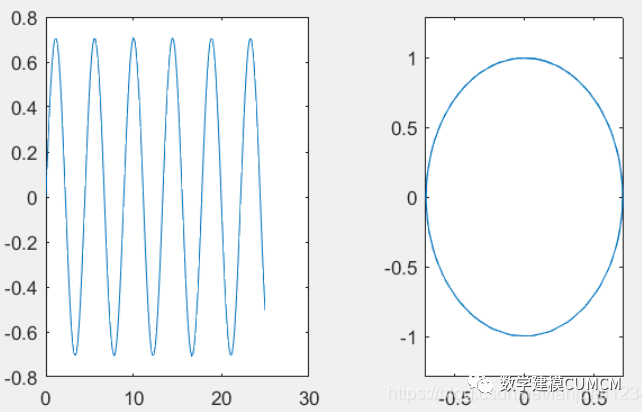
function f = fan(t,x)
f=[-2*x(2);x(1)];
end

tf=25;
[t,y]=ode45('fan',[t0,tf],[1,0]);
subplot(121);
plot(t,y(:,2))
subplot(122);
plot(y(:,2),y(:,1))
axis equal

 

　审核编辑：汤梓红