RF至位解决方案可为材料分析应用提供精密的相位和幅度数据

Ryan Curran, Qui Luu, 和 Maithil Pachchigar

在分析远程站点的材料时，无法把探针放进材料中，此时，高频收发器为准确量化材料的体积分数提供了一种可行的方法，而且不存在直接接触材料时的不利影响。正交调解器为测量这些应用的幅度和相移提供了一种强大的新方法。这里谈到的接收器信号链采用ADL5380宽带正交解调器、 ADA4940-2超低功耗、低失真、全差分ADC 驱动器和AD7903双通道、差分、16 位、1 MSPS PulSAR® ADC，不但可以提供准确的数据，同时还能确保操作的安全性和经济性。

在图1 所示接收器中，一个连续波信号从发射(Tx)天线发出，通过待分析的材料，到达接收(Rx)天线。接收到的信号将相对于原始发射信号进行衰减和相移处理。该幅度变化和相移可用来确定媒介内容。

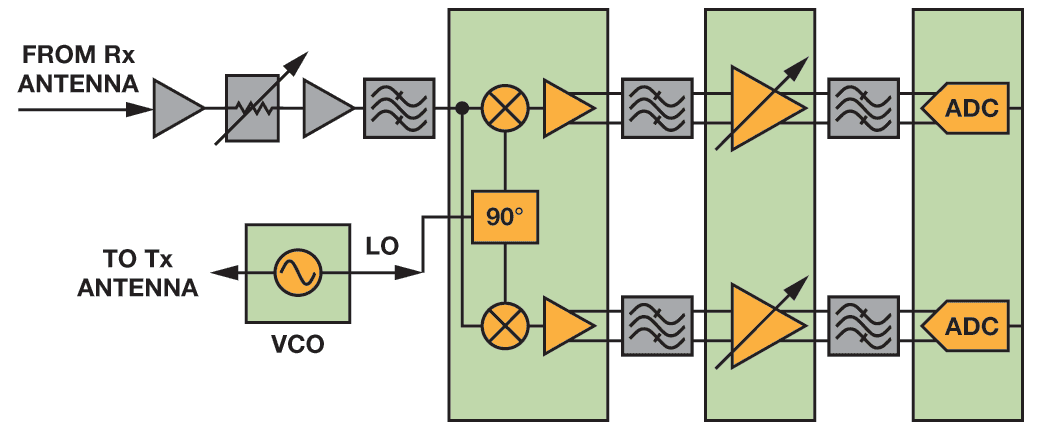
图1. 接收机功能框图

幅度和相移可以直接关联元件的透射率和反射率属性，如图2 所示。举例来说，在油气水流中，对于介电常数、损耗和分散度而言，水高，油低，气超低。

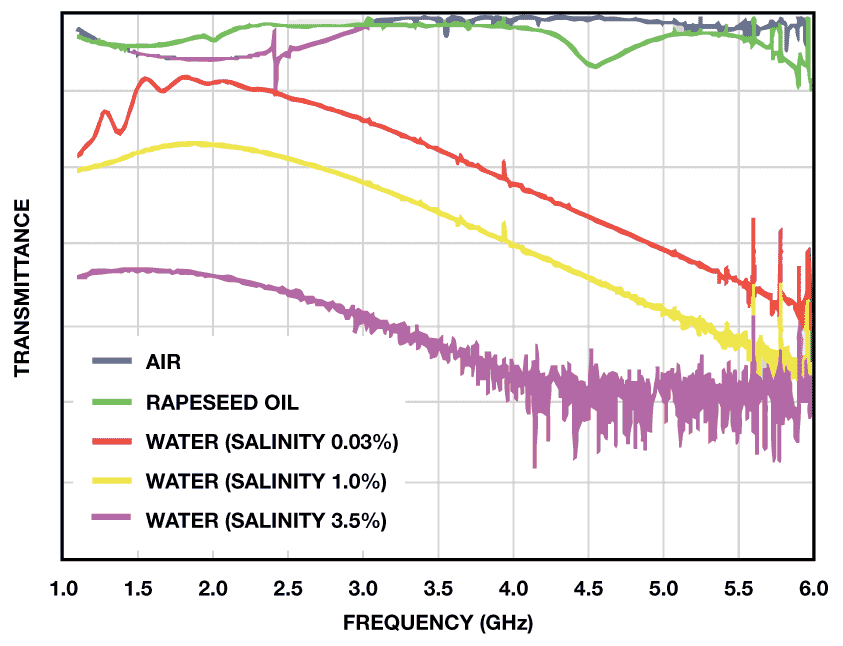
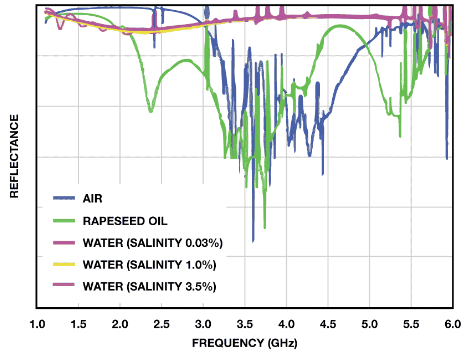
图2. 不同均质媒介的透射率和反射率

接收器子系统的实现

图3 所示接收器子系统把RF 信号转换成数字信号，以精确测量幅度和相位。信号链由一个正交解调器、一个双通道差分放大器和一个双通道差分SAR ADC 构成。这种设计的主要目的是在高频RF输入动态范围较大的条件下，获得高精度的相位和幅度测量结果。

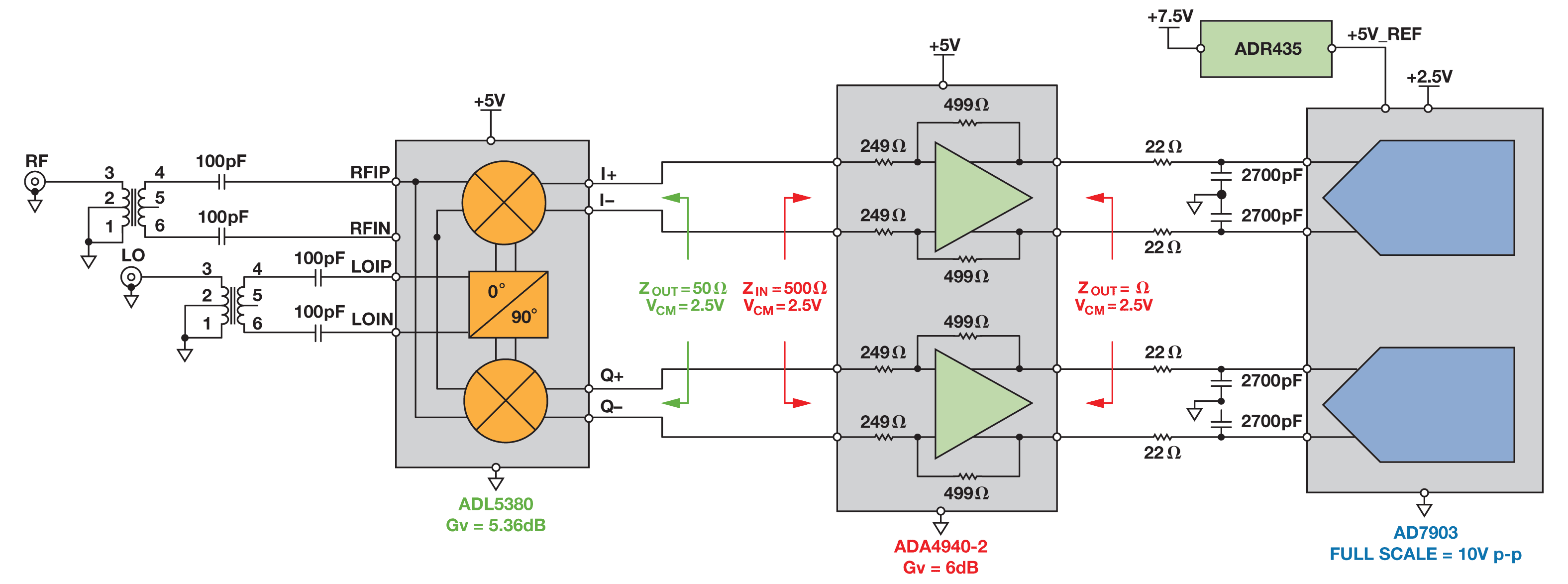
图3. 面向材料分析的接收器简化子系统

正交解调器

正交解调器提供一个同相(I)信号和一个正好反相90°的正交(Q)信号。I 和Q 信号为矢量，因此，可以用三角恒等式计算接收信号的幅度和相移，如图4 所示。本振(LO)输入为原始发射信号，RF 输入为接收信号。解调器生成一个和差项。两个信号的频率完全相同，ωLO = ωRF，因此，结果会过滤掉高频和项，差项则驻留于直流。接收信号的相位为ϕRF，不同于发射信号的相位ϕLO。该相移为ϕLO – ϕRF，是媒介介 电常数导致的结果，有助于确定材料内容。

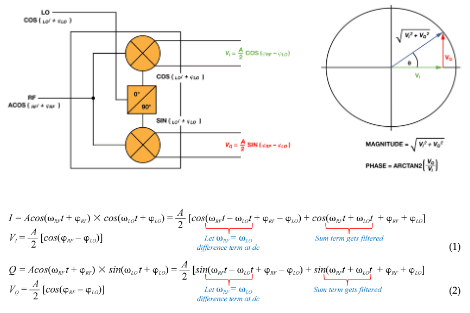
图4. 利用正交解调器测量幅度和相位

真实I/Q 解调器具有许多缺陷，包括正交相位误差、增益不平衡、LO-RF 泄漏等，所有这些都会导致解调信号质量下降。要选择解调器，首先确定RF 输入频率范围、幅度精度和相位精度要求。

ADL5380 采用5 V 单电源供电，可接受400 MHz 至6 GHz 范围内的RF 或IF 输入频率，是接收器信号链的理想选择。根据配置，可提供5.36 dB 电压转换增益，其差分I 和Q 输出可以把2.5 V p-p差分信号驱动至500 Ω 负载。在900 MHz 时，其噪声系数为10.9 dB，IP1dB 为11.6 dBm，三阶交调截点(IIP3)为29.7 dBm，动态范围出色；而0.07 dB 的幅度平衡和0.2°的相位平衡则可实现杰出的解调精度。采用高级SiGe 双极性工艺制造，提供微型4 mm × 4 mm、24 引脚LFCSP 封装。

ADC 驱动器和高分辨率精密ADC

ADA4940-2 全差分双通道放大器具有卓越的动态性能和可调输出共模，是驱动高分辨率双通道SAR ADC 的理想之选。该器件采用5 V 单电源供电，在2.5 V 共模下可提供±5 V 差分输出。根据配置可提供2 倍增益(6 dB)，并把ADC 输入驱动至满量程。RC滤波器(22 Ω/2.7 nF)有助于限制噪声，减少来自ADC 输入端容性DAC 的反冲。采用专有SiGe 互补双极性工艺制造，提供微型4 mm× 4 mm、24 引脚LFCSP 封装。

AD7903 双通道16 位1 MSPS 逐次逼近型ADC 具有出色的精度，满量程增益误差为±0.006%，失调误差为±0.015 mV。该器件采用2.5 V 单电源供电，1 MSPS 时功耗仅12 mW。使用高分辨率ADC的主要目标是实现±1°的相位精度，尤其是当输入信号的直流幅度较小时。ADC 所要求的5 V 基准电压源由ADR435低噪声基准电压源产生。

如图5 所示，接收器子系统利用ADL5380-EVALZ, EB-D24CP44-2Z, EVAL-AD7903SDZ, 和 EVAL-SDP-CB1Z评估套件实现。这些电路组件针对子系统中的互连优化。两个高频锁相输入源提供RF 和LO 输入信号。

图5. 接收器子系统评估平台

表1 总结了接收器子系统中各个组件的输入和输出电压电平。在 解调器的RF 输入端，11.6 dBm 的信号产生的输入在ADC 满量程 范围的–1 dB 之内。表中假定，ADL5380 的负载为500 Ω，转换增 益为5.3573 dB，功率增益为–4.643 dB，ADA4940-2 的增益为6 dB。 该接收器子系统的校准程序和性能结果将在后续章节讨论。

表1. 接收器子系统各组件的输入和输出电压电平

 

RF 输入 (dBm)	ADL5380 输出		AD7903 输入 (dBFS)
	(dBm)	(V p-p)
+11.6	+6.957	4.455	–1.022
0	–4.643	1.172	–12.622
–20	–24.643	0.117	–32.622
–40	–44.643	0.012	–52.622
–68	–72.643	466µ	–80.622

 

接收器子系统误差校准

接收器子系统有三个主要误差源：失调、增益和相位。

I 和Q 通道的各个差分直流幅度与RF 和LO 信号的相对相位存在 正弦关系。因此，I 和Q 通道的理想直流幅度可以通过以下方式计算得到：

 

 

 

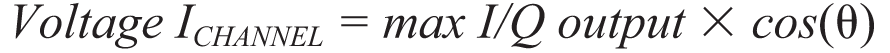
(3)

 

 

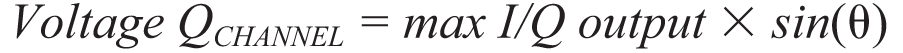
(4)

 

随着相位移过极化坐标，理想状况下，有些位置会产生相同的电 压。例如，I（余弦）通道上的电压应与+90°或–90°相移相同。然而，对于本应产生相同直流幅度的输入相位，恒定相移误差（不受RF 和LO 的相对相位影响）会导致子系统通道产生不同结果。这种情况如图6 和图7 所示，其中，当输入应为0 V 时，结果产生了两个不同的输出码。这种情况下，–37°的相移远远大于含有锁相环的真实系统的预期值。结果，+90°实际上表现为+53°，–90°表现为–127°。

通过10 个步骤从–180°到+180°收集结果，其中，未校正数据产生图6 和图7 所示椭圆形。通过确定系统中的额外相移量，可以解决该误差问题。表2 显示，系统相移误差在整个传递函数范围内都是恒定不变的。

表2. 接收器子系统在0-dBm RF 输入幅度条件下的实测相移小结

 

输入相位 RF至LO	平均I 通道输出代码	平均Q 通道输出代码	I 通道电压	Q 通道电压	实测相位	实测接收器子系统相移
–180°	–5851.294	+4524.038	–0.893	+0.690	+142.29°	–37.71°
–90°	–4471.731	–5842.293	–0.682	–0.891	–127.43°	–37.43°
0°	+5909.982	–4396.769	+0.902	–0.671	–36.65°	–36.65°
+90°	+4470.072	+5858.444	+0.682	+0.894	+52.66°	–37.34°
+180°	–5924.423	+4429.286	–0.904	+0.676	+143.22°	–36.78°

 

系统相位误差校准

对于图5 所示系统，当步长为10°时，平均实测相移误差为–37.32°。 在已知该额外相移时，可以算出经调整的子系统直流电压。变量 ϕPHASE_SHIFT 定义为观测到的额外系统相移的平均值。相位补偿信 号链中产生的直流电压可以计算如下：

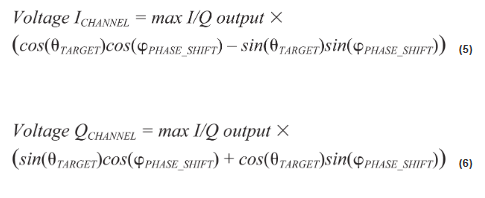
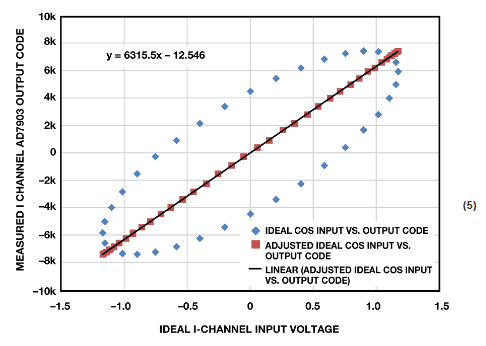
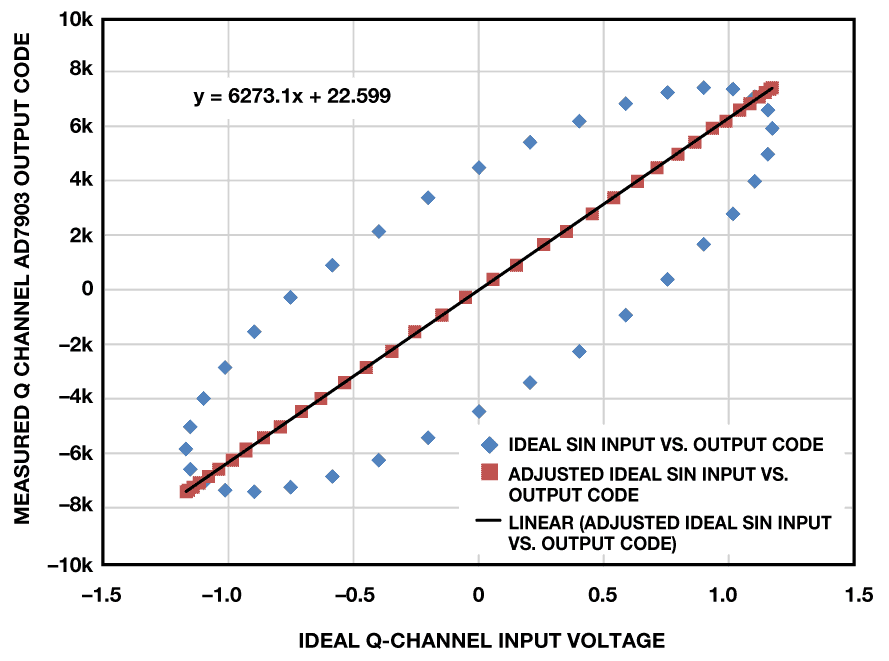
对于给定的相位设置，等式5 和等式6 提供了目标输入电压。现在，子系统已线性化，可以校正失调误差和增益误差了。图6 和图7 中同时显示了线性化的I 和Q 通道结果。对数据集进行线性回归计算，结果将产生图中所示较优拟合线。该拟合线为各个转换信号链的实测子系统传递函数。

 

图6. 线性化的I 通道结果

(5)

 

 

图7. 线性化的Q 通道结果

(6)

 

系统O_set 误差和增益误差校准

接收器子系统中各信号链的理想失调应为0 LSB，但是，对于I通道和Q 通道，实测失调分别为–12.546 LSB 和_22.599 LSB。最优拟合线的斜率代表子系统的斜率。理想子系统斜率可计算如下：

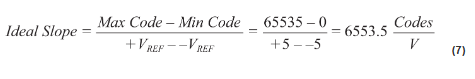
图6 和图7 中的结果表明，I 通道和Q 通道的实测斜率分别为6315.5 和6273.1。为了校正系统增益误差，必须调整这些斜率。校正增益误差和失调误差可以确保，利用等式1 计算得到的信号幅度与理想信号幅度相匹配。失调校正与实测失调误差正好相反：

要计算各子系统信号链的感知模拟输入电压，则须在I 通道和Q通道上使用等式11。利用这些完全调整过的I 通道和Q 通道电压来计算以各直流信号幅度定义的RF 信号幅度。要评估整个校准程序的精度，可以把收集到的结果转换成理想子系统电压，后者产生于调解器输出端，假设条件是不存在相移误差。这可以通过以下方式实现：用前面计算得到的平均直流幅度乘以每次试验的实测相位正弦分数（除掉其中计算得到的相移误差）。计算过程如下：

 

 

 

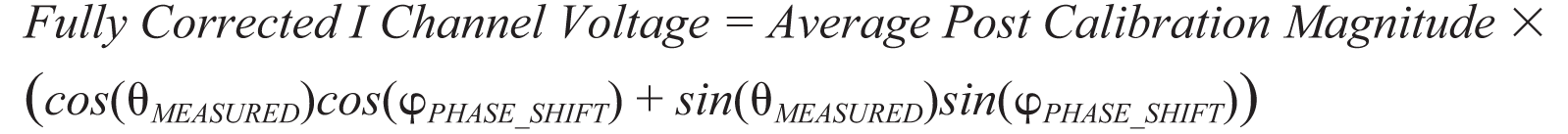
(12)

 

 

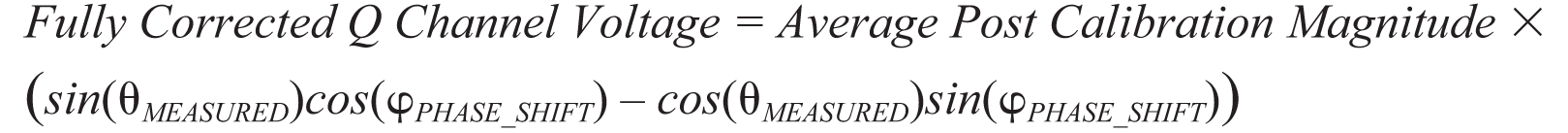
(13)

 

ϕ相移为前面计算得到的相位误差，平均校准后幅度为来自等式1 的 直流幅度结果，已经过失调误差和增益误差补偿。表3 所示为在0 dBm RF 输入幅度条件下，各目标相位输入的校准程序的结果。等式12 和等式13 计算得到的校正因子将集成到旨在以此处所示方式检测相位和幅度的任何系统之中。

接收器子系统评估结果

表3. 0 dBm RF 输入幅度条件下某些目标相位输入端实现的结果。

 

目标相位	I 通道完全校 正输入电压	Q 通道完全校 正输入电压	完全校正相 位结果	绝对实测相位 误差
–180°	–1.172 V	+0.00789 V	–180.386°	0.386°
–90°	–0.00218 V	–1.172 V	–90.107°	0.107°
0°	+1.172 V	+0.0138 V	+0.677°	0.676°
0.676°	+0.000409 V	+1.171 V	+89.98°	0.020°
+180°	–1.172 V	+0.0111 V	+180.542°	0.541°

 

图8 为实测绝对相位误差直方图，其中，对于从–180° 到 +180°的 每10°步长，其精度均高于1°。

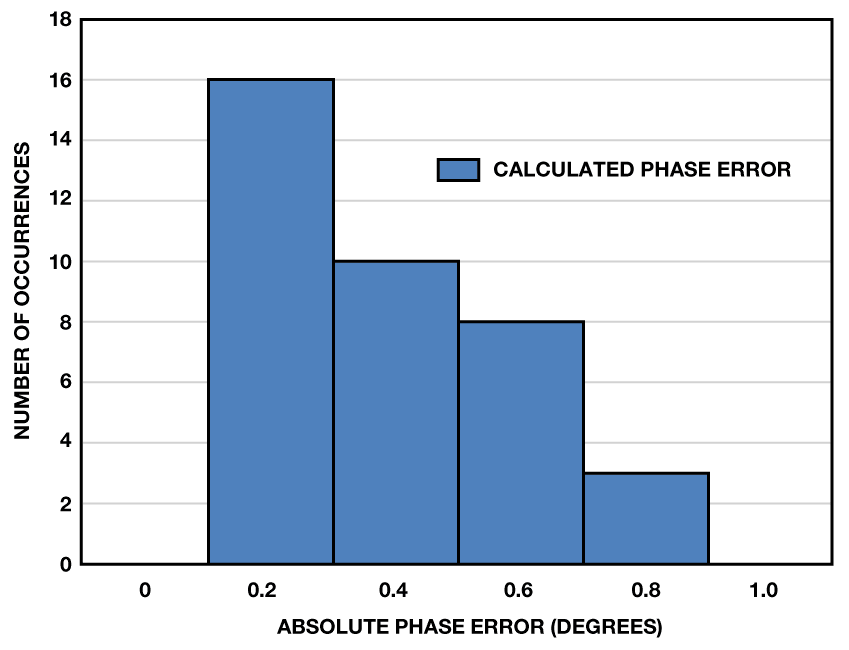
图8. 0 dBm输入电平（相位步长为10°）条件下的实测绝对相位误差直方图

为了在任何给定输入电平条件下精确测量相位，RF 相对于LO 的感知相移误差(ϕPHASE_SHIFT)应恒定不变。如果实测相移误差开始以目标相位步长(ϕTARGET)或幅度函数的形式发生变化，则这里所提校准程序的精度将开始下降。室温下的评估结果显示，900 MHz条件下，对于最大值为11.6 dBm、最小值约为–20 dBm 的RF 幅度而言，相移误差保持相对恒定。

图9 所示为接收器子系统的动态范围以及相应幅度导致的额外相位误差。当输入幅度降至–20 dBm 以下时，相位误差校准精度将开始下滑。系统用户需要确定可接受的信号链误差水平，以确定可接受的最小信号幅度。

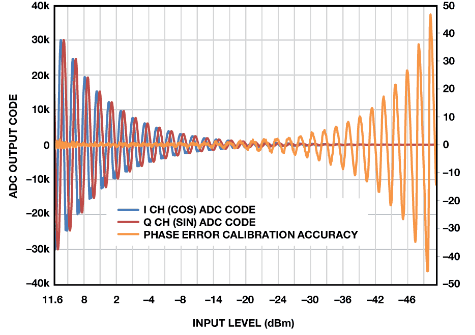
图9. 接收器子系统的动态范围以及相应的额外相位误差

图9 所示结果用5 V ADC 基准电压源收集。该ADC 基准电压源的幅度可以降低，从而为系统提供更小的量化水平。这样，在小信号条件下，相位误差精度会略有提升，但会增加系统饱和几率。为了提高系统动态范围，另一种不错的选择是采用一种过采样方案，该方案可以提高ADC 的无噪声位分辨率。求均值的采样每增加一倍，结果可使系统分辨率增加½ LSB。给定分辨率增量的过采样比计算方法如下：

 

 

 

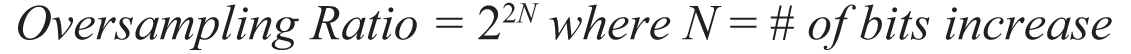
(14)

 

当噪声幅度不再能随机改变各采样的ADC 输出代码时，过采样会达到一个效益递减点。在该点时，系统的有效分辨率将不能再次提升。过采样导致的带宽下降并非大问题，因为系统是以缓慢变化的幅度测量信号的。

AD7903 评估软件提供一个校准程序，允许用户针对三个误差源，对ADC 输出结果进行校正：相位、增益和失调。用户需要收集系统未经校正的结果，确定本文计算的校准系数。图10 所示为图形用户界面，其中，校准系数已高亮显示。 系数一旦确定，则可利用这个面板来计算解调器的相位和幅度。极化坐标为观测到的RF 输入信号提供了一种直观的呈现方式。幅度和相位计算通过等式1 和等式2 计算。用"采样数(Num Samples)"下拉框，通过调整每次捕获的采样数，可实现对过采样比的控制。

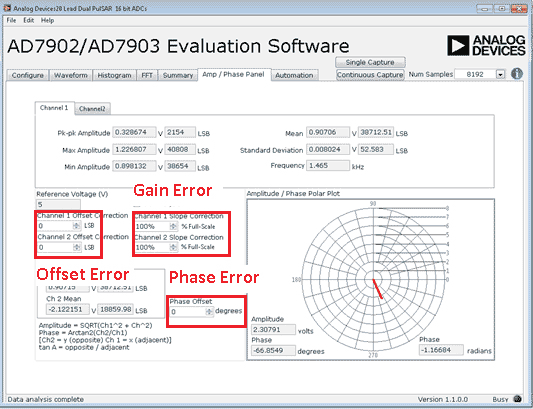
Figure 10. Receiver subsystem calibration GUI.

结论

本文探讨了远程检测应用面临的主要挑战，并提出了一种利用ADL5380、ADA4940-2 和AD7903 接收器子系统的新型解决方案，该方案可以精确、可靠地测量材料内容。提出的信号链具有宽动态范围的特点，在900 MHz 条件下，可实现0°至360°的测量范围，精度优于1°。

审核编辑：郭婷