Buck变换器稳态分析原则

变换器稳态分析原则

前言：以Buck变换器为例，对小纹波近似、电感伏秒平衡以及电容安秒平衡进行解释说明。

图1所示为Buck变换器，所有器件均视为理想元件，电感两端电压及电容电流参考方向如图中所示。

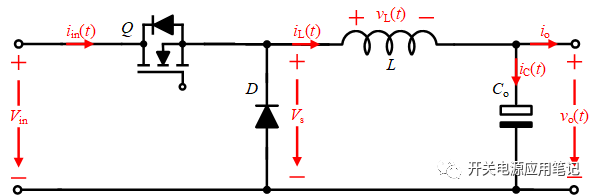
图1 Buck变换器

傅立叶分析：周期波形的直流分量等于其平均值。所以在电路中，可以通过傅立叶分析求得平均值来求解变换器周期波形的直流分量。图2所示为Buck变换器开关端口电压波形，图2(a)为Vs时域波形，当占空比D=0.5时，对时域波形进行傅立叶变换可得如图2(b)所示的Vs频域波形。由图2(b)可知，周期性开关电压除了包含fs=0的直流分量外，还含有开关频率交流成分谐波。而对电压型变换器而言，设计的目的在于获得稳定的输出电压（即：期望输出电压仅含直流量不含交流量），因此，可通过对变换器添加LC滤波器（如：Buck变换器的输出电感和电容）滤除开关频率谐波而获得想要的直流分量。

（注：此处所述LC滤波器仅为变换器内部的LC元件，且LC截止频率远小于开关频率；而对于两级电路架构之间的LC滤波器，其作用更多体现在前级变换器输出端口与后级变换器输入端口之间的阻抗匹配，其目的在于消除前后级之间的低频耦合，此时的截止频率与前后级变换器控制的开关频率相关性较小。）

图2 开关端口电压波形

所以傅立叶分析求解电路表达式（如电压型变换器的输出电压）的过程过于繁琐，因此在稳态条件下，通过引入小纹波近似来推导电感的伏秒平衡和电容的安秒平衡（或电荷平衡），以对变换器进行直接分析。

01小纹波近似

何为小纹波近似？小纹波近似是指在稳态条件下，当波形中的交流纹波分量幅值远小于其中的直流分量大小时，忽略交流纹波分量，对电路进行分析时将实际波形近似等效成仅含直流分量，此过程简称小纹波近似（或线性纹波近似）。

小纹波近似为何只能用于连续波形（如：CCM下的电感电流和电容电压），而不能用于断续波形（如：开关电压、开关电流或电感电压）？对于稳态下的连续波形，其组成可看成直流分量叠加一个由于低通滤波器对开关谐波不完全衰减而引起的交流纹波分量；而对于不连续波形，由于波形本身仅含交流纹波分量而不含直流量，因此无法忽略交流纹波，所以小纹波近似并不适用。

（注：所以DCM下，分析电容电压时小纹波近似可用，但是分析电感电流时不能直接使用，需采用广义状态平均法来分析。）

此外，在对变换器波形的分析中，如果开关周期比电路的固有时间常数（主要指变换器中滤波器的响应时间）小很多，则小纹波近似合理。

02电感伏秒平衡

图3所示为稳态下的电感电流、电压以及输出电压波形。实际输出电压vo( t )由直流分量和交流纹波分量构成：

 

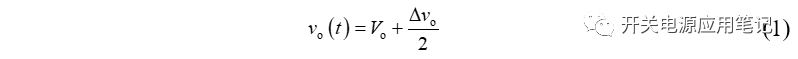
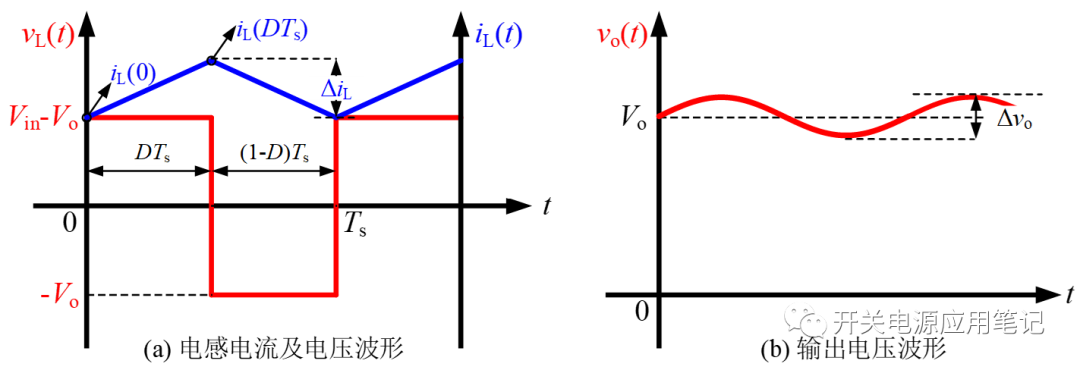
图3 电感电流、电压及输出电压波形

实际设计中，输出电压纹波分量幅值远小于直流分量幅值（如：Δvo≤1%Vo），即：

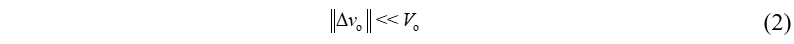
利用小纹波近似，可得：

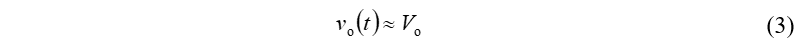
图4所示为Buck变换器在开关管导通和关断状态下的等效电路。利用小纹波近似做开关管导通期间和关断期间的分析。

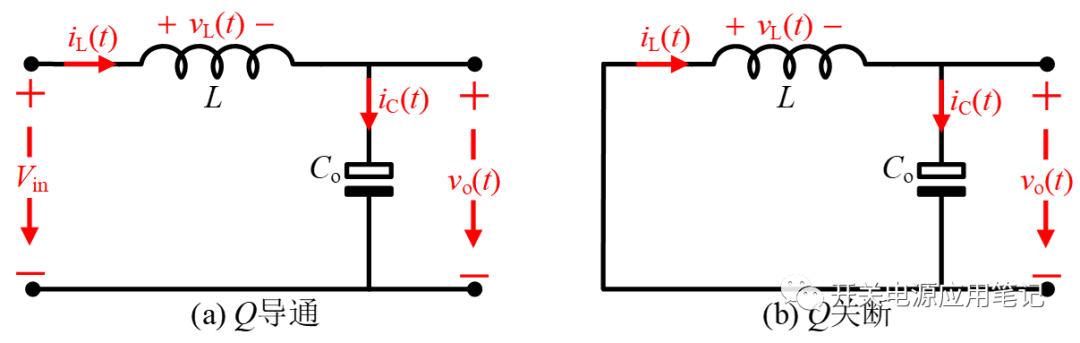
图4 Buck变换器开关状态等效电路

①开关管导通期间，电感两端电压vL(t)为：
 

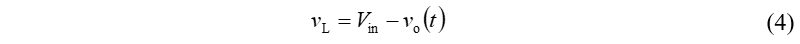
利用小纹波近似，可得：

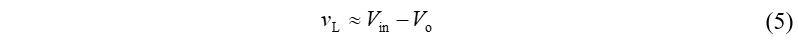
所以在开关管导通期间，电感两端电压基本恒定，其与电流的关系为：

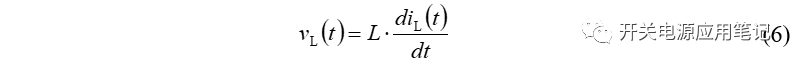
进而可得电感电流上升斜率为：

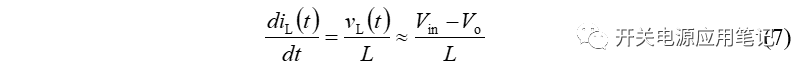
因为上升斜率恒定，所以电感电流线性增加。

②在开关管关断期间，电感两端电压vL(t)为：

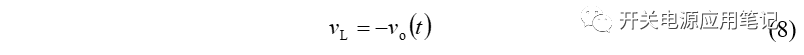
利用小纹波近似，可得：

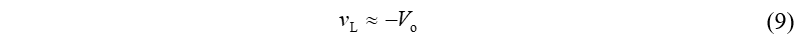
所以在开关管关断期间，电感两端电压同样恒定，可得电感电流下降斜率为：

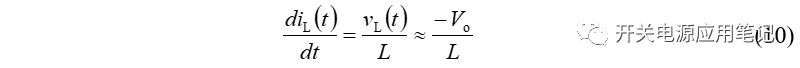
因为下降斜率恒定，因此电感电流线性减小。

结合式(7)、式(10)以及图3，可得稳态下电感电流峰值与谷值差值ΔI为：

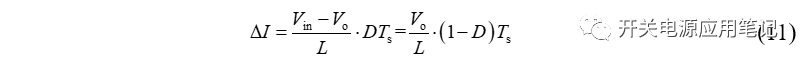
进而可得电感感量为：

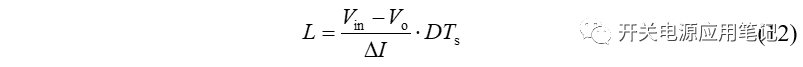
以上分析均在稳态条件下利用小纹波近似对变换器进行分析；在暂态时，变换器工作过程分析如下。

图5所示为电感电流的暂态过程波形。假设在t=0时，变换器开始工作，则电感电流和输出电压初始状态均为0。
 

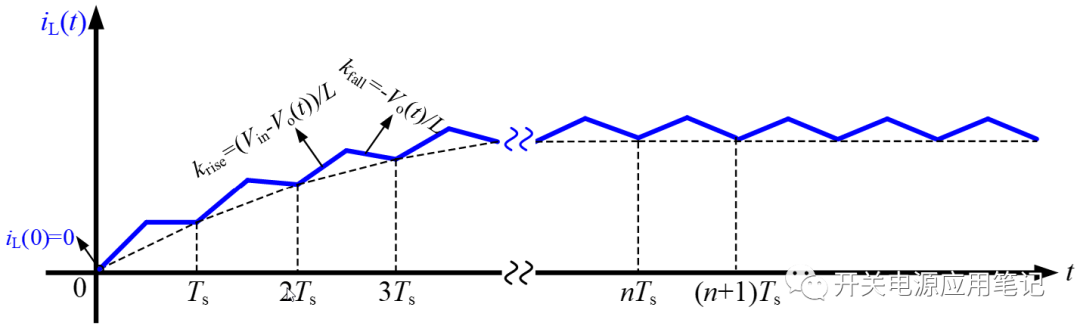
图5 电感电流暂态过程波形

在第一个开关周期内，开关管导通期间，输出电压为0，则电感两端电压为：

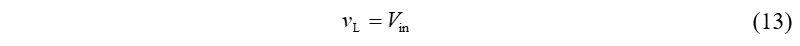
电感电流上升斜率krise最大，为：

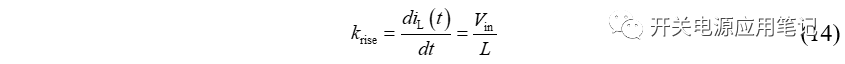
开关管关断期间，电感两端电压为：

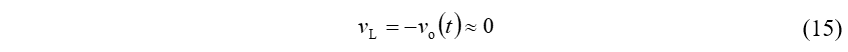
电感电流下降斜率kfall最小，为：

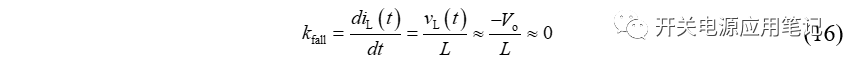
因此，在第一个开关周期内，电感电流呈净增加，即：iL(Ts)-iL(0)>0。在整个暂态过程中，电感电流终值≠初始值（因为t=0时电感电流为0，而要使得电感能够储备能量，在暂态过程中的每一个周期内，电感电流的终值都一定大于初始值），所以无法利用二者相等的条件求解电路的状态方程，在暂态过程中只能逐步迭代去求解任意时刻的电流值（在整个暂态过程中，电感电流在开关管导通期间的上升斜率由最大值逐渐减小，在开关管关断期间的下降斜率由最小值逐渐增大，直至电感电流净增量为0达到稳态）。

由于电感电流流向输出端，所以输出电容被充电，电容电压也逐渐建立。在电感电流迭代的同时，输出电容电压也在迭代（在整个暂态过程中，电容电压在开关管导通期间上升斜率由最大值逐渐减小，在开关管关断期间下降斜率由最小值逐渐增大，直至电容电压净增量为0达到稳态）。

当变换器达到稳态时时，每个开关周期中电感电流与电容电压的终值和初始值之间的关系为：

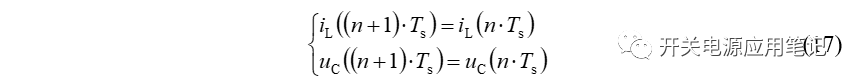
在一个开关周期内，对式(6)中的等号两端同时积分：

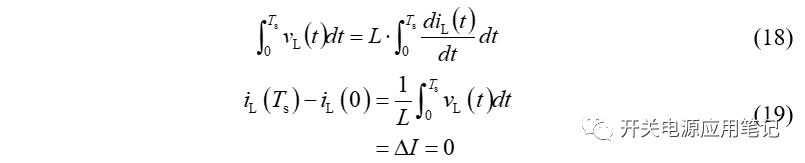
可得，在稳态条件下，施加在电感两端电压的积分一定为0，即电感电压vL(t)在一个周期下的总面积为0或伏秒积为0，称此为伏秒平衡。
 

将式(19)两端同时除以Ts，可得：

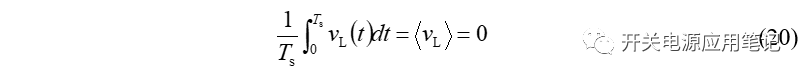
对图3中电感电压积分求得总面积 S ：

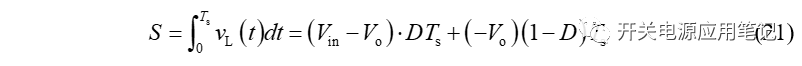
则电感两端平均电压为：

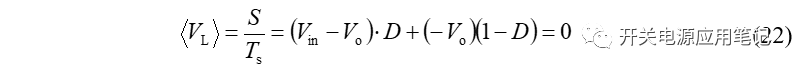
由式(22)可得输出电压表达式为：

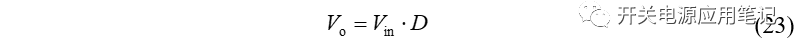
因此，通过电感的伏秒平衡可以推导出变换器输出电压的直流分量表达式，且其具有通用性，即其适用于任何变换器，只需勾勒出施加在电感上的电压波形，利用其平均值为0即可。

03电容安秒平衡

电容电流表达式为：

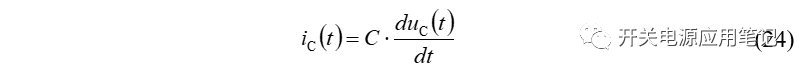
对式(24)中的等号两端同时积分，可得：

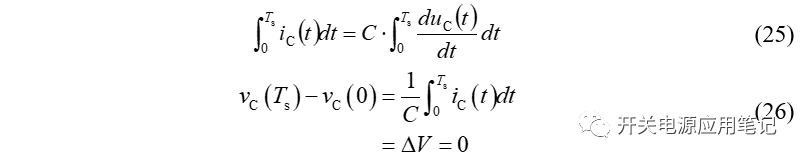
可得，在稳态条件下，施加在电容两端的电流积分一定为0，即电容电流iC(t)在一个周期下的总面积为0或安秒积为0，称此为安秒平衡。
 

将式(26)两端同时除以Ts，可得电容平均电流为：

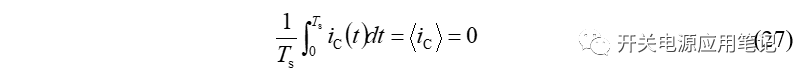
通过电容的安秒平衡可以推导出变换器稳态电流表达式。

总结：如果对电感施加直流电压，则磁通量将持续增加，电感电流将无限制地增加；如果向电容器施加直流电流，则电容器将连续充电，其电压将无限增加。因此在稳态条件下，电感一定满足伏秒平衡，电容一定满足安秒平衡。