数字信号处理：DSP系统设计入门课程

David Skolnick 和 Noam Levine

如果您已经阅读了本系列的第1部分（或者已经熟悉DSP处理实际信号的一些方法），您可能想详细了解如何使用DSP实现数字滤波器（如第1部分中描述的滤波器）。本文是系列文章的第二篇，介绍以下 DSP 主题：

建模过滤器变换函数

将模型与 DSP 架构相关联

尝试使用数字滤波器

本系列旨在从希望将DSP添加到其设计库中的模拟系统设计人员的角度来描述这些主题。使用本系列文章中的信息作为介绍，设计人员可以就何时DSP设计可能比模拟电路更高效做出更明智的决策。

建模过滤器转换函数

第1部分比较了模拟和数字滤波器的特性，并提出了为什么可以通过数字方式（使用DSP）实现这些滤波器;本部分重点介绍数字滤波器应用的一些机制。

使用数字滤波的三个主要原因是（1）更接近理想滤波器近似值，（2）能够在软件中调整滤波器特性，而不是通过物理调谐，以及（3）滤波器响应与采样数据的兼容性。第1部分介绍的两个最著名的滤波器是有限脉冲响应（FIR）和无限脉冲响应（IIR）类型。FIR 滤波器响应称为有限响应，因为它的输出仅基于一组有限的输入样本;它是非递归的，没有极点，在其S平面上只有零。另一方面，IIR滤波器的响应可以无限期地持续（并且可能不稳定），因为它是递归的，即其输出值受到输入和输出的影响。它的 s 平面上有极点和零点。图 1 显示了第 1 部分中出现的典型滤波器架构和求和公式。

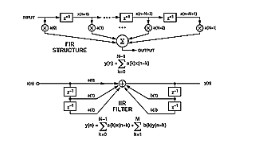
图1.滤波器方程及其延迟线模型。

要对这些过滤器进行数字建模，可能需要两个步骤。首先，将这些公式视为在计算机上运行的程序。此步骤包括将公式分解为数学步骤（例如，乘法和加法），并确定计算机执行所需的所有其他操作（处理指令和数据，测试状态等）以在软件中实现公式。

其次，将这些操作编写为程序。这可能是一项相当艰巨的任务。幸运的是，有很多“预制”软件可用，通常是像C这样的高级语言（HLL），在某种程度上简化了（但绝不是消除！）编程工作。不过，从学习的角度来看，从汇编语言开始可能更有启发性;此外，汇编语言算法通常比必须优化系统性能的 HLL 更有用。在某些高级语言的抽象级别，程序可能看起来不太像方程。例如，图 2 显示了作为 C 程序实现的 FIR 算法的示例。

float fir_filter(float input, float *coef, int n, float *history)

{

int i;

float *hist_ptr, *hist1_ptr, *coef_ptr;

float output;

hist_ptr = history;

hist1_ptr = hist_ptr; /* use for history update */

coef_ptr = coef + n -1; /* point to last coef */

/*form output accumulation */

output = *hist_ptr++ * (*coef_ptr-);

for(i = 2; i < n; i++)

{

*hist1_ptr++ = *hist_ptr; /* update history array */

output += (*hist_ptr++) * (*coef_ptr-);

}

output += input * (*coef_ptr); /* input tap */

*hist1_ptr = input; /* last history */

return(output);

}

有许多支持算法建模的分析包可用;请参阅本文末尾的参考资料，了解几个流行的软件包。在本系列的不同时间，我们将回到算法建模。现在，继续讨论该过程，在这些滤波器算法建模之后，它们就可以在DSP架构中实现了。

将模型与DSP架构相关联：对于编程，必须了解DSP架构的四个部分：数字、存储器、序列器和I/O操作。此体系结构讨论是通用的（适用于一般 DSP 概念），但它也是具体的，因为它与本文后面的编程示例相关。图 3 显示了本节介绍的通用 DSP 架构。

建筑

数字部分：由于 DSP 必须在单个指令周期内完成乘法/累加、加、减和/或位移运算，因此针对数字运算优化的硬件是所有 DSP 处理器的核心。正是这种硬件将DSP与通用微处理器区分开来，通用微处理器可能需要许多周期才能完成这些类型的操作。在数字滤波器（和其他DSP算法）中，DSP必须完成涉及数据值和系数的多个算术运算步骤，以实时产生通用处理器无法实现的响应。

数字运算发生在DSP的乘法/累加器（MAC）、算术逻辑单元（ALU）和桶形移位器（移位器）中。MAC执行乘积总和运算，这些运算出现在大多数DSP算法（如FIR和IIR滤波器以及快速傅里叶变换）中。ALU 功能包括加法、减法和逻辑运算。对位和字的操作发生在移位器内。图 3 显示了 MAC、ALU 和移位器的并行度，以及数据如何流入和流出它们。

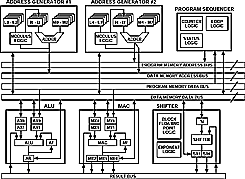
图3.有用的 DSP 架构。

从编程的角度来看，使用单独数字部分的DSP架构提供了极大的灵活性和效率。数据有许多不冲突的路径，允许单周期完成数值运算。DSP的架构还必须为MAC操作提供宽动态范围，能够处理两倍于输入宽度的乘法结果，以及可以安装而不会溢出的累加器输出。（在 16 位 DSP 上，此功能相当于 MAC 的 16 位数据输入和 40 位结果输出。需要此范围来处理大多数DSP算法（例如滤波器）。

数字部分的其他功能可以促进实时系统中的编程。通过使操作依赖于由数值运算产生的各种条件状态，这些状态可以作为程序执行、进位、溢出、饱和、标志或其他状态测试中的变量。使用这些条件，DSP 可以根据数值运算快速处理有关程序流的决策。需要不断将数据馈送到数字部分，这是影响DSP存储器和内部总线结构的关键设计因素。

内存部分：DSP存储器和总线架构设计以速度需求为导向。数据和指令必须在每个指令周期流入DSP的数字和排序部分。不能有延误，不能有瓶颈。设计的所有内容都集中在吞吐量上。

 

哈佛和冯诺依曼架构的词源 - 根据弗吉尼亚理工大学计算机科学系的John A. N. Lee： 哈佛系列机器的开发者霍华德·艾肯（Howard Aiken）坚持在他的所有机器中分离数据和程序。在我最熟悉的Mark III中，他甚至为每个鼓准备了不同尺寸的鼓。 “冯·诺依曼的概念是，通过将指令视为数据，可以对程序进行更改，增强程序'学习'的能力。 “出于某种原因，后者被赋予了冯·诺依曼的名字，而前者的名字来自哈佛大学的机器系列。”

 

为了正确看待吞吐量，可以看看DSP存储器设计与其他微处理器存储器之间的区别。大多数微处理器使用包含数据和指令的单个存储器空间，使用一条总线作为地址，另一条用于数据或指令。这种架构被称为冯诺依曼架构。冯诺依曼架构中对吞吐量的限制来自于必须在每个周期的一段数据或一条指令之间进行选择。在DSP中，存储器通常分为程序存储器和数据存储器，每个存储器都有单独的总线。这种类型的架构被称为哈佛架构。通过分离数据和指令，DSP可以在每个周期中获取多个项目，从而使吞吐量翻倍。指令缓存、结果反馈和上下文切换等其他优化也提高了 DSP 吞吐量。

DSP 存储器架构中的其他优化与重复存储器访问有关。大多数DSP算法（如数字滤波器）需要以重复访问模式从存储器中获取数据。通常，这种类型的访问用于从一系列地址中获取数据，该范围充满了来自要处理的真实信号的数据。通过减少“管理”存储器访问所需的指令数量（开销），DSP可以“保存”指令周期，从而为每个周期处理信号的主要工作留出更多时间。为了减少开销并自动管理这些类型的访问，DSP 利用专用数据地址生成器 （DAG）。

大多数DSP算法要求在单个周期内从存储器中获取两个操作数，以成为算术单元的输入。为了以灵活的方式提供这两个操作数的地址，DSP 有两个 DAG。在DSP改进的哈佛架构中，一个地址生成器通过数据存储器地址总线提供地址;另一个通过程序存储器地址总线提供地址。通过为下一条数字指令及时执行这两个数据获取，DSP能够维持指令的单周期执行。

DSP算法（例如示例数字滤波器）通常需要对地址范围（缓冲区）中的数据进行寻址，以便地址指针从缓冲区的末尾“环绕”回缓冲区的开头（缓冲区长度）。此指针移动称为循环缓冲。（在滤波器方程中，每个求和基本上都是由数据点循环缓冲区和系数循环缓冲区的乘法累加序列得出的）。循环缓冲的变体（在某些应用程序中是必需的）将地址指针推进每个“步长”大于一个地址的值，但仍以给定长度环绕。这种变化称为模循环缓冲。

通过其DAG支持各种类型的缓冲，DSP能够在硬件中执行地址修改和比较操作，以实现最佳效率。在软件中执行这些功能（如在通用处理器中发生）会限制处理器处理实时信号的能力。

由于缓冲是一个不寻常的概念，但却是数字信号处理的关键，因此一个简短的缓冲示例非常有用。在图 4 所示的示例中，从地址 30 开始，内存中驻留了八个位置的缓冲区。地址生成器必须计算保留在此缓冲区内的下一个地址，但保持适当的数据间距，以便跳过两个位置。地址生成器将地址 30 输出到地址总线上，同时将地址修改为 33 以进行下一个周期的内存访问。此过程重复，在缓冲区中移动地址指针。当地址 36 修改为 39 时，会出现特殊情况。地址 39 位于缓冲区外部。地址生成器检测到地址已落在缓冲区边界之外，并将地址修改为 31，就像缓冲区的末尾连接到缓冲区的开头一样。更新、比较和修改不会产生任何开销。在一个周期内，地址36被输出到地址总线上。在下一个周期，地址31被输出到地址总线上。这种模循环缓冲可满足插值滤波器等算法的需求，并节省处理指令周期。

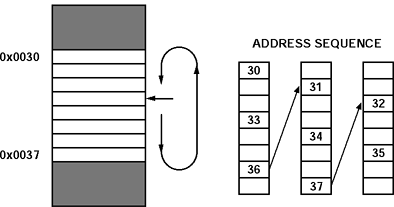
图 4.模循环缓冲示例。

音序器部分：由于大多数DSP算法（例如示例滤波器）本质上是重复的，因此DSP的程序序列器需要循环遍历重复的代码，而不会产生开销，同时从循环的结束返回到循环的开始。此功能称为零开销循环。能够在没有开销的情况下进行环路是DSP与传统微处理器区别的一个关键领域。通常，微处理器要求在软件中维护程序循环，在循环的末尾放置条件指令。此条件指令确定地址指针是移动（跳转）回循环顶部还是另一个地址。由于从存储器中获取这些地址需要时间，而信号处理时间的可用性在DSP应用中至关重要，因此DSP不能浪费周期以这种方式检索条件程序排序（分支）的地址。相反，DSP 在硬件中执行这些测试和分支功能，存储所需的地址。

如图5所示，DSP在一个周期内执行环路的最后一条指令。在下一个周期，DSP评估条件并执行循环顶部的第一条指令或环路外的第一条指令。由于 DSP 使用专用硬件进行这些操作，因此不会在软件评估条件、检索地址或分支程序执行上浪费额外的时间。

图5.程序循环示例。

输入/输出 （I/O） 部分：正如一再指出的那样，需要向DSP提供巨大的数据吞吐量;关于其设计的所有内容都集中在将数据汇集到数字、内存和序列器部分。数据的来源和输出的目的地（信号处理的结果）是DSP与其系统和现实世界的连接。完成信号处理任务需要许多I/O功能。非 DSP 存储器阵列存储处理器指令和数据。通信通道（如串行端口、I/O 端口和直接存储器访问 （DMA）通道）将数据快速传入和传出 DSP。其他功能（如定时器和程序启动逻辑）简化了DSP系统开发。DSP 系统中典型 I/O 任务的简要列表包括以下内容（以及许多其他任务）：

引导加载：在复位时，DSP通常通过外部存储器接口从外部源（EPROM或主机）加载指令。

串行通信：DSP 通过同步串行端口 （SPORT） 接收或传输数据，与编解码器、ADC、DAC 或其他设备通信。

内存映射 I/O：DSP 通过外部设备解码的非 DSP 存储器位置接收或传输数据。

试验数字滤波器

在对滤波器算法进行建模并查看了一些DSP架构特性之后，人们准备开始研究如何用DSP汇编语言对这些滤波器进行编码。到目前为止，讨论和示例都是通用的，几乎适用于所有DSP。此处的示例特定于ADI公司的ADSP-2181。该处理器是一个定点、16 位 DSP。术语“定点”是指分隔尾数和指数的“点”在算术运算期间不会改变其位位置。定点DSP的编程可能更具挑战性，但它们往往比浮点DSP便宜。“16位DSP”中的“16位”是指DSP数据字的大小。该DSP使用16位数据字和24位宽指令字。DSP 由数据大小而不是指令宽度指定，因为数据字大小描述了 DSP 可以最有效地处理的数据宽度。

该软件有两个部分。主例程包括寄存器和缓冲区初始化以及中断向量表，以及数据样本准备就绪时执行的中断例程。初始化后，DSP 在主例程中执行指令，执行一些后台任务、循环访问代码或在低功耗待机模式下空闲，直到从 A/D 转换器获得中断。在此示例中，处理器在低功耗待机模式下空闲，等待中断。

FIR 滤波器中断子例程（代码的最后一段）是滤波器程序的核心。处理器响应中断，保存主例程的上下文并跳转到中断例程。此中断例程处理滤波器输入样本，从存储器读取数据和滤波器系数，并将其存储在DSP处理器的数据寄存器中。处理输入样本后，DSP将输出样本发送到D/A转换器。

.module/RAM/ABS=0 FIR_PROGRAM;

/******** Initialize Constants and Variables *****************/

.const taps=127;

.var/dm/circ data[taps];

.var/pm/circ fir_coefs[taps];

.init fir_coefs: ;

.var/dm/circ output_data[taps];

/******** Interrupt vector table *****************************/

reset_svc: jump start; rti; rti; rti;

/*00: reset */

irq2_svc: /*04: IRQ2 */

si=io(0); /* get next sample */

dm(i0,m0)=si; /* store in tap delay line */

jump fir; /* jump to fir filter */

nop; /* nop is placeholder */

irql1_svc: rti; rti; rti; rti; /*08: IRQL1 */

irql0_svc: rti; rti; rti; rti; /*0c: IRQL0 */

sp0tx_svc: rti; rti; rti; rti; /*10: SPORT0 tx */

sp0rx_svc: rti; rti; rti; rti; /*14: SPORT1 rx */

irqe_svc: rti; rti; rti; rti; /*18: IRQE */

bdma_svc: rti; rti; rti; rti; /*1c: BDMA */

sp1tx_svc: rti; rti; rti; rti; /*20: SPORT1 tx or IRQ1 */

sp1rx_svc: rti; rti; rti; rti; /*24: SPORT1 rx or IRQ0 */

timer_svc: rti; rti; rti; rti; /*28: timer */

pwdn_svc: rti; rti; rti; rti; /*2c: power down */

/******* START OF PROGRAM - initialize mask, pointers **********/

start:

/* set up various control registers */

ICNTL=0x07; /* set IRQ2, IRQ1, IRQ0 edge sensitive */

IFC=0xFF; /* clear all pending interrupts */

NOP; /* add nop because of one cycle */

/* synchronization delay of IFC */

SI=0x0000;

DM(0x3FFF)=SI; /* sports not enabled */

/* sport1 set for IRQ1, IRQ0, FI, FO */

IMASK=0x200; /* enable IRQ2 interrupt */

i0=^data; /* index to data buffer */

l0=taps; /* length of data buffer */

m0=1; /* post modify value */

i4=^fir_coefs; /* index to fir_coefs buffer */

l4=taps; /* length of fir_coefs buffer */

m4=1; /* post modify value */

i2=^output_data; /* index to data buffer */

l2=taps; /* length of data buffer */

cntr=taps;

do zero until ce;

dm(i0,m0)=0; /* clear out the tap delay data buffer */

zero: dm(i2,m0)=0; /* clear out the output_data buffer */

/**** WAIT for IRQ2 Interrupt - then JUMP to INTERRUPT VECTOR **/

wait: idle; /* wait for IRQ2 interrupt */

jump wait;

/******* FIR FILTER interrupt subroutine ***********************/

fir cntr=taps-1; /* set up loop counter */

mr=0, mx0=dm(i0,m0), my0=pm(i4,m4);

/* fetch data and coefficient */

do fir1loop until ce; /* set up loop */

fir1loop: mr=mr+mx0*my0(ss), mx0=dm(i0,m0), my0=pm(i4,m4);

/* calculations */

/* if not ce jump fir1loop;*/

mr=mr+mx0*my0(rnd); /* round final result to 16-bits */

if mv sat mr; /* if overflow, saturate */

io(1)=mr1; /* send result to DAC */

dm(i2,m0)=mr1;

rti;

/******* END OF PROGRAM *************************************/

.endmod;

请注意，此程序使用 DSP 功能，这些功能以零开销执行操作，通常由条件引入。特别是，程序循环和数据缓冲区以零开销进行维护。滤波器循环核心中的多功能指令执行乘法/累加运算，同时从内存中获取下一个数据字和滤波器系数。

程序检查过滤器计算的最终结果是否有任何溢出。如果最终值溢出，则该值将饱和以模拟模拟信号的削波。最后，恢复主例程的上下文，并通过中断返回 （RTI） 指令将指令流返回到主例程。

查看和预览

本文的目的是提供滤波器理论与数字滤波器实现之间的联系。在此过程中，本文将介绍如何使用 HLL 程序对滤波器进行建模、使用 DSP 架构以及试验滤波器软件。本文介绍的问题包括：

过滤器作为程序

DSP 架构（通用）

DSP 汇编语言

由于这些问题涉及许多有价值的细节级别，在这篇简短的文章中无法公正地描述，因此您应该考虑阅读Richard Higgins的文本，VLSI中的数字信号处理和Paul Embree的文本，实时DSP的C算法（见下面的参考文献）。这些文本提供了DSP理论，实现问题和实践简化（发布时可用的设备）的完整概述，以及练习和示例。下面的参考部分还包含进一步放大本文问题的其他来源。为准备本系列的下一篇文章，您可能需要免费获取ADSP-2100系列用户手册*或ADSP-2106x SHARC用户手册。 这些文本提供有关ADI公司的定点和浮点DSP架构的信息，这是这些文章的主要主题。在本系列中，每个部分都增加了一些功能或信息，有助于实现开发DSP系统的系列目标。

审核编辑：郭婷