数字信号处理：DSP系统设计入门课程

在听过很多关于数字信号处理（DSP）技术的知识之后，您可能想了解DSP可以做什么，研究为什么DSP在许多类型的操作中比模拟电路更受欢迎，并了解如何学到足够的知识来设计自己的DSP系统。本文是系列文章的第一篇，是朝着寻找问题的答案迈出重要的第一步的机会。本系列从寻求更多工具处理模拟信号的模拟系统设计人员的角度介绍DSP主题。阅读本系列的设计人员可以了解DSP处理模拟信号的可能性，以及在哪里可以找到其他信息和帮助来源。

什么是DSP？简而言之，DSP是处理器或微型计算机，其硬件、软件和指令集针对高速数字处理应用进行了优化，这对于实时处理表示模拟信号的数字数据至关重要。DSP的作用很简单。例如，当充当数字滤波器时，DSP根据信号样本接收数字值，计算对这些值进行操作的滤波器功能的结果，并提供代表滤波器输出的数字值;它还可以根据这些值的属性提供系统控制信号。DSP的高速算术和逻辑硬件经过编程，可快速执行模拟滤波器变换的算法。

提供这种能力的设计元素算术运算符、存储器处理、指令集、并行性、数据寻址的组合构成了 DSP 与其他类型的处理器之间的关键区别。了解实时信号和DSP计算速度之间的关系，为这种组合的特殊性提供了一些背景知识。实时信号作为一系列来自模数转换器（ADC）的单个样本进入DSP。为了实时进行滤波，DSP必须在下一个样本到达之前完成处理每个样本所需的所有计算和操作（通常更新涉及许多先前样本的过程）。为了对具有大量频率内容的真实信号执行高阶滤波，需要真正快速的处理器。

为什么要使用 DSP？

为了了解DSP的计算类型，并了解模拟电路与DSP系统的比较情况，可以根据滤波器功能比较这两个系统。熟悉的模拟滤波器使用电阻器、电容器、电感器、放大器。它可以便宜且易于组装，但难以校准、修改和维护随过滤器顺序呈指数级增长的难度。出于多种目的，使用DSP可以更轻松地设计、修改和依赖滤波器，因为DSP上的滤波器功能基于软件、灵活且可重复。此外，要创建具有高阶响应的灵活可调滤波器，只需修改软件，与纯模拟电路不同，无需额外的硬件。理想的带通滤波器具有图1所示的频率响应，具有以下特性：

通带内的响应完全平坦，相移为零

阻带中的无限衰减。
有用的补充包括：

通带调谐和宽度控制

阻带滚降控制。

如图1所示，使用二阶滤波器的模拟方法需要相当多的交错高Q值部分;调整和调整它的难度可想而知。

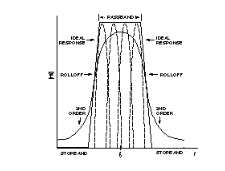
图1.理想的带通滤波器和二阶近似。

使用DSP软件，滤波器设计有两种基本方法：有限脉冲响应（FIR）和无限脉冲响应（IIR）。FIR滤波器对脉冲的时间响应是当前和有限数量的先前输入样本的直接加权和。在没有反馈的情况下，当样品到达“线的末端”时，它对给定样品的响应结束（图2）。FIR滤波器的频率响应没有极点，只有零点。相比之下，IIR 滤波器被称为无限，因为它是一个递归函数：它的输出是输入和输出的加权和。由于它是递归的，因此它的响应可以无限期地继续。IIR滤波器频率响应具有极点和零点。

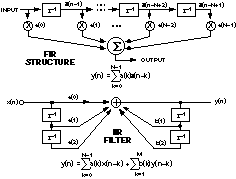
图2.滤波器方程和延迟线表示。

xs 是输入样本，ys 是输出样本，as 是输入样本权重，bs 是输出样本权重。n 是当前采样时间，M 和 N 是编程的采样数（滤波器的顺序）。请注意，为这两种类型指示的算术运算只是总和和乘积，可能数量很大。事实上，乘加法是许多DSP算法的情况，这些算法表示非常精密和复杂的数学运算。

近似理想滤波器包括应用具有适当系数和足够高阶数或抽头数的传递函数（将输入样本序列视为抽头延迟块）。图3显示了90抽头FIR滤波器与各种阶次锐截止切比雪夫滤波器的响应。90抽头示例表明滤波器可以接近理想滤波器的程度。在DSP系统中，对图90所示的3抽头FIR滤波器进行编程并非易事。相比之下，使用纯模拟电路尝试这种近似水平并不具有成本效益。支持使用DSP近似理想滤波器的另一个关键点是长期稳定性。使用FIR（或具有足够分辨率以避免截断误差累积的IIR），可编程DSP可以一次又一次地实现相同的响应。高阶纯模拟滤波器响应随时间推移不太稳定。

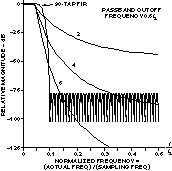
图3.90抽头FIR滤波器响应与尖锐截止切比雪夫滤波器的响应相比。

数学变换理论和实践是创建DSP应用和理解其局限性的核心要求。本系列文章通过几个信号分析和处理示例来介绍DSP概念。该系列还提供了进一步研究的文本参考，并确定了简化信号处理软件开发的软件工具。

对真实信号进行采样

现实世界的现象模拟了声音、光、热、电、磁等物理过程不断变化的能级。传感器将这些电平转换为可管理的电压和电流信号，ADC对这些信号进行采样并将其转换为数字信号进行处理。ADC的转换速率或采样频率在实际信号的数字处理中至关重要。

该采样率由为给定应用充分处理信号所需的信号信息量决定。为了使ADC提供足够的样本来准确描述实际信号，采样速率必须至少是模拟信号最高频率分量的两倍。例如，为了准确描述包含高达20 kHz频率的音频信号，ADC必须以至少40 kHz的频率对信号进行采样。由于到达信号很容易包含高于20 kHz的元件频率（包括噪声），因此在采样之前，必须通过ADC之前的低通滤波器馈送信号来消除它们。该滤波器称为抗混叠滤波器，旨在消除20 kHz以上可能破坏转换信号的频率。

但是，抗混叠滤波器的频率滚降有限，因此必须为滤波器的过渡带提供额外的带宽。例如，输入信号带宽为 20 kHz 时，可能允许 2 到 4 kHz 的额外带宽。

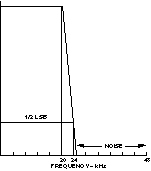
图4.抗混叠滤波器理想响应。

图4显示了抑制频率高于48 kHz采样速率一半的任何信号所需的滤波器。抑制意味着衰减到ADC分辨率的1/2最低有效位（LSB）以下。在没有高度复杂的模拟滤波器的情况下实现这种抑制水平的一种方法是使用过采样转换器，例如Σ-Δ型ADC。它通常以兆赫兹速率获得低分辨率（例如，1位）样本，比最高频率分量的两倍快得多，大大减轻了对转换器前面的模拟滤波器的要求。内部数字滤波器（工作中的DSP！）恢复所需的分辨率和频率响应。对于许多应用，过采样转换器可减少系统设计工作量和成本。

处理真实信号

ADC采样速率取决于被采样模拟信号的带宽。此采样率设定了可供处理的样本的速度。一旦系统带宽要求确定了A/D转换器采样速率，设计人员就可以开始探索DSP处理器的速度要求。

所需采样率下的处理速度受算法复杂性的影响。通常，DSP需要在接收第二个样本之前完成与第一个样本相关的所有操作。采样间隔时间是DSP执行所有处理任务的时间预算。对于音频示例，48 kHz 采样率对应于 20.833 μs 采样间隔。图5显示了模拟信号和数字采样速率。

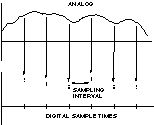
图5.采样训练和处理时间。

接下来考虑DSP的速度与算法（包含变换或其他数字运算集的软件）的复杂性之间的关系。复杂的算法需要更多的处理任务。由于样品之间的时间是固定的，因此复杂性越高，处理速度越快。例如，假设该算法要求在样本之间执行 50 个处理操作。使用前面示例的 48 kHz 采样率（20.833 μs 采样间隔），可以计算所需的最低 DSP 处理器速度，以每秒百万次操作 （MOPS） 为单位，如下所示：

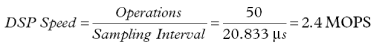
因此，如果样本之间的所有时间都可用于实现算法的操作，则需要性能级别为 2.4 MOPS 的处理器。请注意，基于每秒操作数 （MOPS） 和每秒指令数 （MIPS） 的 DSP 的两个常见额定值并不相同。具有 10-MIPS 额定值的处理器，每条指令可以执行 8 个操作，其性能与具有 40 MIPS 额定值的更快处理器的性能基本相同，每个指令只能执行 2 个操作。

对各种真实信号进行采样

有两种基本方法可以获取数据，一次一个样本或一次一个帧（连续处理与批处理）。基于样本的系统，如数字滤波器，一次采集一个样本的数据。如图6所示，在时钟的每个时钟周期，一个样本进入系统，并输出一个处理后的样本。输出波形不断发展。

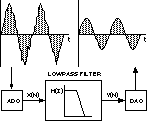
图6.在数字滤波器中连续处理样品的示例。

基于帧的系统，如频谱分析仪，用于确定时变波形的频率分量，获取帧（或样本块）。处理发生在整个数据帧上，并生成转换后的数据帧，如图 7 所示。

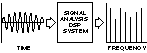
图7.数据块的批处理示例。

对于 48 kHz 的音频采样率，处理 1024 个样本帧的处理器的帧采集间隔为 21.33 毫秒（即 1024 x 20.833 μs = 21.33 毫秒）。在这里，DSP有21.33毫秒的时间来完成该数据帧所需的所有处理任务。如果系统实时处理信号，则不得丢失任何数据;因此，当DSP处理第一帧时，它也必须获取第二帧。数据采集是DSP特殊架构特性发挥作用的一个领域：处理器灵活的数据寻址功能与其直接存储器访问（DMA）通道相结合，有助于实现无缝数据采集。

响应真实世界的信号

不能假设样本之间的所有时间都可用于执行处理指令。实际上，必须为处理器准备时间以响应外部设备，从而控制数据的进出。通常，外部设备（如ADC）使用中断向处理器发出信号。DSP对该中断的响应时间或中断延迟直接影响实际信号处理的剩余时间。

中断延迟（响应延迟）取决于几个因素;最主要的是DSP架构的指令流水线。指令流水线由接收中断和程序执行恢复之间发生的指令周期数组成。DSP 中的流水线级别越高，中断延迟就越长。例如，如果处理器的周期时间为 20 ns，并且需要 10 个周期来响应中断，则在执行任何信号处理指令之前需要 200 ns。

当一次采集一个样本的数据时，如果DSP在下一个样本到达之前完成对每个样本的处理，则200 ns开销不会受到伤害。然而，当在一次处理一帧时逐个样本地采集数据时，中断的系统会浪费处理器指令周期。例如，运行基于帧的算法（如FFT）的中断响应时间为200 ns的系统，帧大小为1024个样本，将需要204.8 μs的开销。这相当于浪费了超过10，000个指令周期，以延迟DSP可以执行信号处理的生产时间。在具有DMA和双存储器访问等架构特性的DSP中，这种浪费很容易避免;它们使DSP在不中断处理器的情况下接收和存储数据。

开发数字数字信号处理器系统

在讨论了处理器、ADC、抗混叠滤波器的作用以及这些组件之间的时序关系之后，现在是时候了解一个完整的DSP系统了。图8显示了可用于数据采集和控制的典型DSP系统的构建模块。

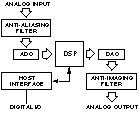
图8.将 DSP 系统的元素组合在一起。

请注意，组成DSP系统的组件很少，因为系统的大部分功能都来自可编程DSP。转换器将数据漏入和漏出DSP;ADC时序由精密采样时钟控制。为了简化系统设计，目前可用的许多转换器器件都结合了以下部分或全部功能：A/D转换器、D/A转换器、采样时钟以及用于抗混叠和抗成像的滤波器。这些类型的I/O组件中的时钟振荡器由外部晶体单独控制。以下是有关此类DSP系统中数据流的一些要点：

模拟输入：模拟信号由抗混叠滤波器适当限制频带，并施加到ADC的输入端。在选定的采样时间，转换器中断DSP处理器并使数字采样可用。ADC和DSP之间的串行和并行接口之间的选择取决于数据量、设计复杂性权衡、空间、功耗和价格。

数字信号处理：传入的数据由DSP的算法软件处理。当处理器完成所需的计算时，它将结果发送到DAC。由于信号处理是可编程的，因此在处理数据和通过增量编程调整提高系统性能方面具有相当大的灵活性。

模拟输出：DAC在下一个采样时钟将DSP的输出转换为所需的模拟输出。转换器的输出由低通抗成像滤波器（也称为重建滤波器）平滑，以产生重建的模拟信号。

主机接口：可选的主机接口允许DSP与外部系统通信，发送和接收数据和控制信息。

本文旨在概述主要的DSP设计概念，并解释为什么DSP更适合某些应用的模拟电路的一些原因。本文介绍的问题包括：

数字信号处理器概述

实时数字数字信号处理器操作

真实信号

采样率和抗锯齿滤波

DSP 算法时间预算

样本驱动数据采集与帧驱动数据采集

由于这些问题涉及许多有价值的细节级别，我们无法在这篇简短的文章中公正地对待，因此您应该考虑阅读Richard Higgins的文本，VLSI中的数字信号处理（请参阅下面的参考文献）。本文提供了DSP理论、实现问题和实践简化（发布时可用的设备）的完整概述，以及练习和示例。下面的参考部分还包含进一步放大本文问题的其他来源。为准备本系列的下一篇文章，您可能需要免费获取ADSP-2100系列用户手册*和ADSP-2106x SHARC用户手册。 这些文本提供有关ADI公司的定点和浮点DSP架构的信息，这是这些文章的主要主题。下一篇文章将涵盖以下领域：

信号处理的数学概述：它将介绍整个系列中出现的变换函数（频域）和卷积函数（时域）的数学原理。虽然数学处理必然是不完整的（没有推导），但将有足够的细节来考虑如何对操作进行编程。

数字信号处理器架构：本文将讨论DSP的算术逻辑单元（ALU）、乘法累加器（MAC）、桶移器和存储器总线的性质和功能，并描述支持DSP功能的数值运算。

DSP编程概念：对编程的讨论将把理论和实践（数学和建筑）结合在一起。最后，它将列出串联长度DSP设计项目的主要参数，作为示例提供。

审核编辑：郭婷