高性能、低成本电子秤的参考设计

Colm Slattery 和 Mariah Nie

        电子秤向更高精度和更低成本的方向发展，对低成本高性能模拟信号处理的需求不断增加。此要求的范围并不明显;大多数电子秤以1：3，000或1：10，000的分辨率输出最终重量值，这很容易通过12位至14位ADC（模数转换器）满足。然而，对电子秤的仔细检查表明，满足分辨率要求并不容易实现;事实上，ADC精度需要接近20位。在本文中，我们将讨论电子秤的一些系统规格，并讨论设计和构建电子秤系统的注意事项。考虑的主要方面是峰峰值噪声分辨率、模数转换器动态范围、增益漂移和滤波。我们将来自实际称重传感器的测量数据与来自稳定基准电压源的输入进行比较，使用电子秤参考设计作为评估板。

称重传感器

最常见的称重秤实现方案是使用桥式称重传感器，其电压输出与放置在其上的重量成正比。典型的称重传感器电桥如图1所示;它是一个具有至少两个可变臂的4电阻桥电路，其中电阻随施加的重量而变化，在2.5 V（电源电压的一半）的共模电平下产生差分电压。典型的电桥将具有 300 欧姆量级的电阻器。

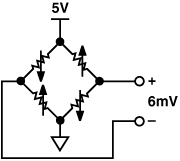
图1.称重传感器的基本电路。

称重传感器本质上是单调的。称重传感器的主要参数是灵敏度、总误差和漂移。

敏感性

典型称重传感器的电灵敏度（定义为满载输出与激励电压之比）为2 mV/V。具有 2mV/V 灵敏度和 5V 激励时，满量程输出电压为 10mV。通常，为了使用称重传感器量程中最线性的部分，只会使用该范围的三分之二左右。因此，满量程输出电压约为6 mV。因此，挑战在于测量6 mV满量程范围内的小信号变化，以获得可实现的最高性能，这在通常使用电子秤的工业环境中并非易事。

总误差

总误差是输出误差与额定输出之比。典型的电子秤的总误差规格约为 0.02%。这是一个非常重要的规格，因为它限制了理想信号调理电路所能达到的精度。因此，它决定了A/D转换器分辨率的选择，以及放大电路和滤波器的设计。

漂移

称重传感器也会随着时间的推移而漂移。图2显示了在24小时内测量的实际称重传感器漂移特性。在测量期间，温度基本上是恒定的，因此漂移与温度无关。所示结果（使用24位ADC测量的位变化数）显示总漂移为125 LSB，或约7.5 ppm。

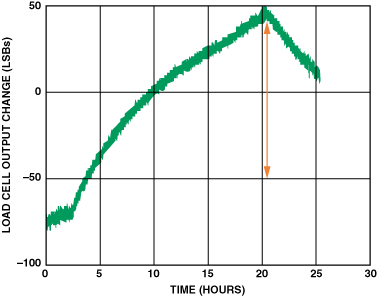
图2.长期称重传感器稳定性—24 小时绘图。

电子秤系统

设计电子秤系统时要考虑的最重要参数是内部计数、ADC动态范围、无噪声分辨率、更新速率、系统增益和增益误差漂移。系统必须设计为比率式，因此与电源电压无关——这将在后面讨论。

内部计数

如前所述，用户看到的典型电子秤系统的分辨率范围从低端的1：3，000到高端解决方案的1：10，000。例如，一个称重秤的重量分辨率可达 5 公斤，计数为 1：10，000，重量分辨率为 0.5 克。此分辨率（如LCD显示屏所示）通常称为外部计数。为了保证准确满足此分辨率，系统的内部分辨率必须至少提高一个数量级。事实上，一些标准规定系统的内部计数比外部计数好 20 倍。对于上面的示例，内部计数需要为 1：200，000。

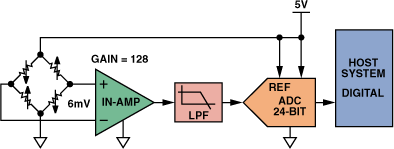
图3.典型的称重系统。

模数转换器动态范围

在使用标准高分辨率A/D转换器的电子秤应用中，不太可能使用ADC的整个满量程范围。在图1的示例中，称重传感器具有5 V电源和10 mV满量程输出。线性范围为6 mV。在前端使用增益为128级时，ADC输入将看到约768 mV满量程。如果使用标准2.5 V基准电压源，则仅使用ADC动态范围的30%。

如果在1 mV满量程范围内，内部计数需要精确到200：000，770，则ADC需要提高3×至4×才能满足性能要求。在这种情况下，对于1：800，000的计数，ADC将需要19位到20位的精度。现在可以理解信号处理要求带来的实际挑战。

增益和失调漂移

工业秤系统通常在 50 摄氏度的温度范围内运行。设计人员必须考虑系统在高于室温的温度下的精度，因为增益随温度漂移可能是误差的主要来源。例如，增益误差漂移为20 ppm/°C的1位稳定系统在50度范围内将具有50 LSB的误差。尽管系统在1°C时可能稳定为25 LSB，但在整个温度范围内实际上只有50 LSB的精度。因此，在设计电子秤时，选择具有低增益漂移的ADC是一个非常重要的考虑因素。

失调漂移不是那么大的考虑因素。大多数Σ-Δ型ADC采用固有的斩波模式技术设计，具有漂移更低、抗1/f噪声能力更强等优点，这对电子秤设计人员非常有用。例如，AD7799模数转换器的失调漂移规格为10 nV/°C。 在 20 位系统中，在整个 1 度工作范围内，总共仅产生 4/50 LSB 误差。

无噪声分辨率

阅读数据手册时的一个常见错误是没有注意噪声是指定为均方根（rms）还是峰峰值（p-p）。对于电子秤应用，最重要的规格是p-p噪声，它决定了无噪声代码分辨率。ADC的无噪声码分辨率是分辨率位数，超过该位数，由于与所有ADC相关的有效输入噪声，无法明确分辨单个代码。该噪声可以表示为均方根量，通常表示为LSB单位的数量（计数，2–n满量程）。乘以 6.6（捕获标准分布中所有值的 99.9%）得到合理的等效峰峰值（以 LSB 表示）。大多数ADI公司的Σ-Δ型ADC数据手册都规定了均方根和峰峰值或无噪声代码，如下表所示，摘自AD7799数据手册。

更新速率

在图4中可以看出，系统的无噪声分辨率取决于ADC的更新速率。例如，使用2.5 V基准电压源和4.17 Hz的更新速率，分辨率为20.5位p-p（增益为128）;而在 500 Hz 时，分辨率降低到 16.5 位。在电子秤系统中，设计人员需要在ADC采样的最低更新速率与更新LCD显示屏所需的输出数据速率之间取得平衡。对于高端电子秤，通常使用10 Hz ADC更新速率。

表I：采用7799.2 V基准电压源时AD5的输出RMS噪声（mV）与增益和输出更新速率的关系

 

更新速率	增益为 1	增益为 2	增益为 4	增益为 8	增益为 16	增益为 32	增益为 64	增益为 128
4.17赫兹	0.64	0.6	0.185	0.097	0.075	0.035	0.027	0.027
8.33赫兹	10.4	0.96	0.269	0.165	0.108	0.048	0.037	0.040
16.7赫兹	1.55	1.45	0.433	0.258	0.176	0.085	0.065	0.065
33.3赫兹	2.3	2.13	0.647	0.364	0.24	0.118	0.097	0.094
62.5赫兹	2.95	2.85	0.952	0.586	0.361	0.178	0.133	0.134
125赫兹	4.89	4.74	1.356	0.785	0.521	0.265	0.192	0.192
250赫兹	11.76	9.5	3.797	2.054	1.027	0.476	0.326	0.308
500赫兹	11.33	9.44	3.132	1.773	1.107	0.5	0.413	0.374

 

表二.AD7799的典型分辨率（位）与增益和输出更新速率的关系

 

更新速率	增益为 1	增益为 2	增益为 4	增益为 8	增益为 16	增益为 32	增益为 64	增益为 128
4.17赫兹	23 (20.5)	22 (19.5)	22.5 (20)	22.5 (20)	22 (19.5)	22 (19.5)	21.5 (19)	20.5 (18)
8.33赫兹	22 (19.5)	21.5 (19)	22 (19.5)	22 (19.5)	21.5 (19)	21.5 (19)	21 (18.5)	20 (17.5)
16.7赫兹	21.5 (19)	20.5 (18)	21.5 (19)	21 (18.5)	21 (18.5)	21 (18.5)	20 (17.5)	19 (16.5)
33.3赫兹	21 (18.5)	20 (17.5)	21 (18.5)	20.5 (18)	20.5 (18)	20.5 (18)	19.5 (17)	18.5 (16)
62.5赫兹	20.5 (18)	19.5 (17)	20.5 (18)	20 (17.5)	19.5 (17)	19.5 (17)	19 (16.5)	18 (15.5)
125赫兹	20 (17.5)	19 (16.5)	20 (17.5)	19.5 (17)	19 (16.5)	19 (16.5)	18.5 (16)	17.5 (15)
250赫兹	18.5 (16)	18 (15.5)	3.797	18 (15.5)	18 (15.5)	18.5 (16)	18 (15.5)	17 (14.5)
500赫兹	18.5 (16)	18 (15.5)	3.132	18 (16)	18 (15.5)	18.5 (16)	17.5 (15)	16.5 (14)

 

图4.AD7799模数转换器的等效输入噪声和分辨率。

电子秤参考设计

选择最佳ADC

用于电子秤应用的最佳ADC架构是Σ-Δ，因为它具有低噪声和低更新速率下的高线性度。另一个好处是噪声整形和数字滤波在片内实现。高频调制器中的集成可形成量化噪声，使噪声被推到调制器频率的一半。然后，数字滤波器将响应限制在明显较低的频率。这大大减少了用户对ADC数据进行复杂后处理的需求。

ADC还应包含一个具有高内部增益的低噪声可编程增益放大器（PGA），以放大称重传感器的小输出信号。与具有外部增益电阻的分立放大器相比，集成PGA可以优化以提供低温度漂。采用分立式配置时，温度漂移引起的任何误差都将通过增益级放大。AD7799专为电子秤应用而设计，具有出色的噪声规格（27 nV/rt-Hz）和最大增益为128 mV/mV的前端增益级。称重传感器可以直接连接到该ADC。

图5是ADI公司设计的电子秤系统评估板参考设计的框图。它由一个AD7799 ADC组成，由ADuC847微控制器控制。除了为AD7799提供数字接口和实现后处理外，ADuC847微控制器本身还包含一个24位、高性能Σ-Δ型ADC。这样，用户就可以比较包含AD7799 ADC的系统与采用ADuC847 ADC的完全独立系统（硬件连接相同）的测试结果，从而选择最能满足要求的设计。

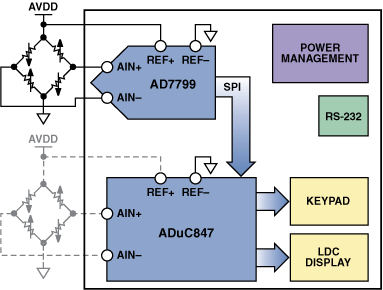
图5.参考设计框图。

测试结果

下图显示了使用电子秤参考设计的一些测试结果。所有结果均基于测量ADC输出代码的标准偏差，实际上是均方根噪声。为了转换为“无噪声分辨率代码”，我们使用以下计算：

标准偏差 = 均方根噪声 （LSB）

峰峰值噪声 = 6.6 × 均方根噪声 （LSB）

以分辨率位为单位的噪声 = log2（p-p 噪声）

ADC 无噪声分辨率（位）= 24 –（以位为单位的噪声）

= 24 – 日志2（6.6 × 均方根噪声 （LSB）） 分辨率位

图6显示了使用基准电压作为ADC输入的测量数据。实测基准的标准分布为3.25 LSB。 乘以6.6计算峰峰值噪声得到21.65 LSB。 将其转换为分辨率位会产生4.42位噪声。对于24位ADC，这意味着19.58位的“无噪声分辨率”。图7显示了在典型称重传感器上完成的相同测试。在这种情况下，“无噪声分辨率”为19.4位。这意味着称重传感器本身只会给最终结果增加0.2位噪声，因此ADC显示为该噪声的主要贡献者。

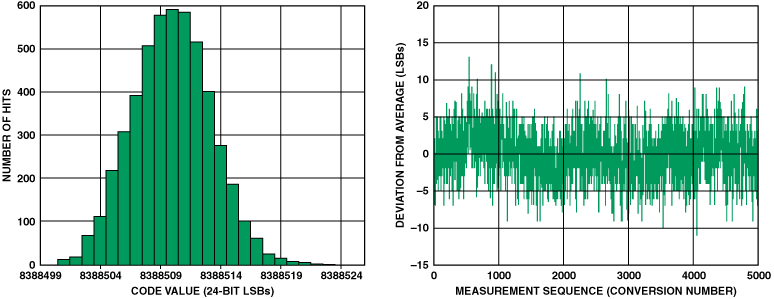
图6.AD7799在以下条件下的噪声性能：增益 = 64，更新速率 = 4.17 Hz，基准电压源 = 5 V，输入短路至基准电压源。RMS 噪声 = 3.2526 LSB，p-p 分辨率 = 19.576 位。

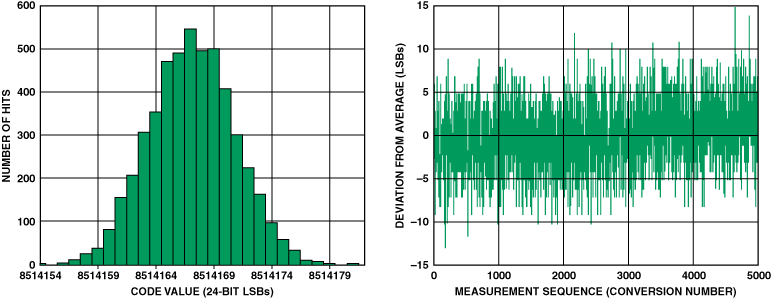
图7.AD7799在以下情况下的噪声性能：增益 = 64，更新速率 = 4.17 Hz，基准电压源 = 5 V，称重传感器输入。RMS 噪声 = 3.6782 LSB，p-p 分辨率 = 19.399 位。

改善ADC结果

低带宽、高分辨率AD7799的分辨率为24位。但是，如上所示，有效位数受噪声限制，具体取决于输出字速率和使用的增益设置。为了提高有效分辨率并尽可能多地消除噪声，ADuC847的微控制器被编程为采用平均算法以获得更好的性能。图8显示了模拟输入接地时从Σ-Δ型ADC获得的典型直方图。理想情况下，对于此固定直流模拟输入，输出代码应为常数。但是，由于噪声，围绕恒定模拟输入值的代码会分散。这种噪声是由ADC内部的热噪声和模数转换过程中固有的量化噪声引起的。代码传播本质上通常是高斯的。

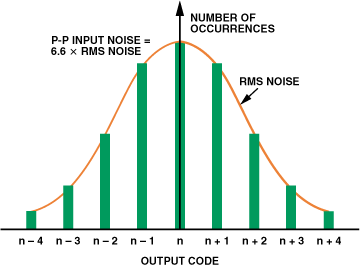
图8.测量恒定模拟输入的ADC的直方图。

平均滤波器是减少随机白噪声同时保持最锐利阶跃响应的好方法。这里讨论的设计软件使用移动平均算法。图 9 显示了基本算法流程。

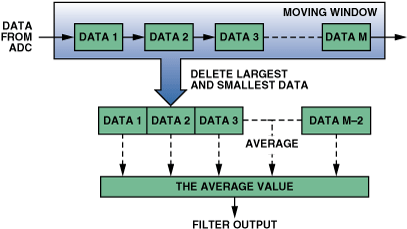
图9.平均算法。

移动平均滤波器对输入信号中的多个点求平均值，以产生输出信号中的每个点。滤波器的输入直接取自ADC。对最新的 M 个数据点进行操作，最小和最大的数据点（异常值）将从数据窗口中删除。其余 M – 2 点取平均值，如公式所示。

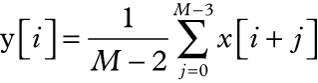
使用移动平均技术，输出数据速率与输入数据速率相同。这是一阶平均。对于更高的更新速率，通常使用二阶平均来降低波形色散。在这种情况下，第一阶段的输出通过第二阶段进行平均，以进一步改善结果。

图10显示了AD7799平均后的实测数据。将其与图 5 进行比较：平均后，最终结果提高了约 2.3 位（21.9 位对 19.6 位有效分辨率）。这种技术可以显著改善最终结果，而不会影响LCD输出更新速率。这种技术的唯一缺点是由于平均的流水线延迟而导致的建立时间较长。

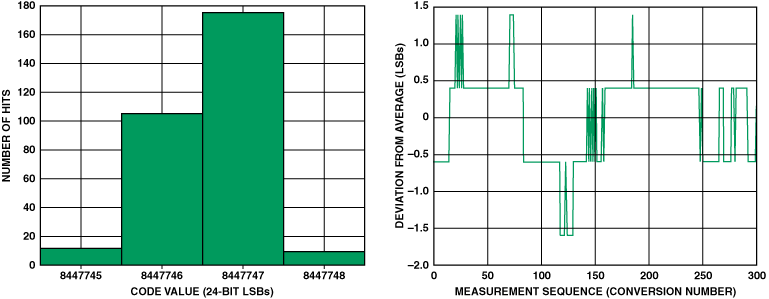
图 10.AD7799滤波后的噪声性能：增益 = 64，更新速率 = 4.17 Hz，基准电压源 = 5 V，称重传感器输入。RMS 噪声 = 0.611 LSB，p-p 分辨率 = 21.9 位。

缩短对重量变化的响应时间

基本算法可以提高噪声性能，但是当权重改变时就出现了问题。重量变化后，称重传感器的输出应在很短的时间内移动到另一个平衡状态。根据算法，滤波器的输出只能在滤波器刷新M次后指示最正确的结果。响应时间受平均点数的限制。需要特定的算法来判断权重的变化。图 11 显示了此算法的基本流程。

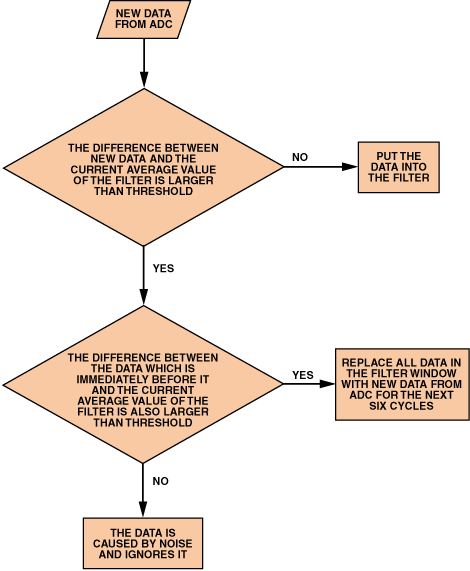
图 11.权重变化判断算法。

首先，使用双倍的判断步骤，以避免将故障视为权重变化。当来自ADC的两个连续数据点和滤波器输出之间的差异都超过阈值时，这被认为是权重变化。

第二阶段的所有M点都将填充相同的新数据，以便在重量变化后非常快速地跳过称重传感器的过渡期。此外，称重传感器本身具有稳定时间。为了弥补这一点，在检测到权重变化后，平均移动窗口中的所有数据将在接下来的六个连续平均周期内使用最新的ADC数据刷新，以传递恢复时间。六个刷新周期后，平均将恢复。

消除输出结果上的闪烁

称重秤对齐以显示 0：5，1 和 1：5，000 标准范围的 1.10 克分度或 000 克分度。当权重位于两个相邻显示权重之间的边距中时，显示将在这些权重之间闪烁。为了保持显示稳定，使用了图12中的算法：

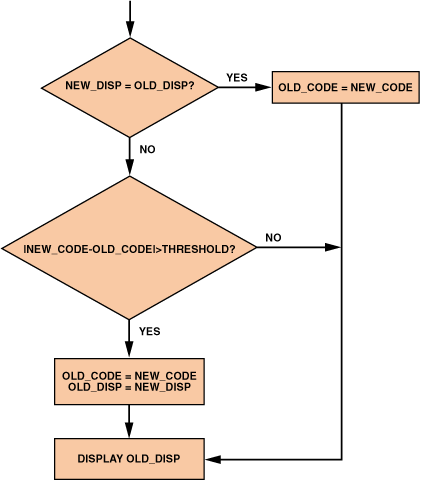
图 12.代码更改流程图。

在每个显示周期中，软件决定此周期中显示的重量是否与前一个周期相同。如果相同，LCD输出将不会改变，并且该过程将继续到下一个周期。如果不同，将计算这两个周期之间的内部代码差异。如果差值小于阈值，则视为噪声效应，因此仍会显示旧权重。如果差值大于阈值，它将更新显示。

比较ADuC847和AD7799 ADC性能

对于低成本电子秤设计，ADuC847及其板载ADC可提供单芯片解决方案。ADuC847集成了一个24位Σ-Δ型ADC和一个8052微控制器内核。内部ADC还具有增益为128 PGA，具有差分模拟输入和基准输入。它还包括 62K 字节的片上程序闪存和 4K 字节的片上数据闪存。下图13和图14中的曲线比较了ADuC847上的集成ADC与噪声较低的独立AD7799。两个测试的条件相同：模拟输入短路至2.5 V基准电压源，增益为64。正如我们所期望的，AD7799具有较低的噪声，因此适合高端应用，而ADuC847则适用于要求较低的电子秤。

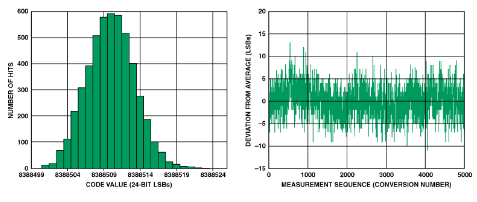
图 13.AD7799噪声性能：增益 = 64，更新速率 = 4.17 Hz，基准电压源 = 5 V，输入短路至基准电压源。RMS 噪声 = 3.2526 LSB，p-p 分辨率 = 19.576 位。

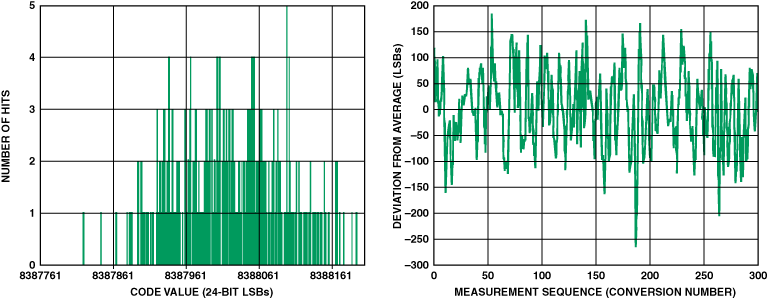
图 14.ADuC847噪声性能：增益 = 64，更新速率 = 5.35 Hz，基准电压源 = 2.5 V，输入短路至基准电压源。RMS 噪声 = 74.65 LSB，峰峰值分辨率 = 15 位，数据手册规格 = 15 位。

电子秤设计注意事项

比率式设计

为了获得最佳性能，参考设计中采用了比率测量技术（用于电桥激励和ADC基准的相同基准源），如图3所示。称重传感器的输出精度由电桥的激励电压决定。电桥输出与激励电压成正比，激励电压的任何漂移都会在输出电压中产生相应的漂移。通过使用与电桥激励电压成比例的电压作为ADC的参考源，如果实际电桥激励电压发生变化，测量精度不会下降。这种比例连接消除了激励源中漂移和极低频噪声的影响。为了滤除来自ADC输入端称重传感器的噪声，可以使用简单的一阶RC滤波器。

布局

布局对于使用高精度Σ-Δ型ADC获得最佳噪声性能至关重要。最重要的两个方面是接地和电源去耦。在此参考设计中，接地层分为模拟和数字部分。AD7799位于这两个接地层之间的分离层上方。一个起点用于连接AD7799正下方的接地层。AD7799的GND引脚应连接到模拟地。在此设计中，仅使用一个电源，但 AVDD 和 DVDD 端子之间有一个铁氧体磁珠。铁氧体磁珠在低频时具有低阻抗，在高频下具有高阻抗。因此，铁氧体磁珠可以阻挡DVDD中的高频噪声。选择铁氧体磁珠时，应研究其阻抗与频率的关系特性。在本设计中，选择600欧姆表面贴装封装的铁氧体磁珠。最后，使用 0.1μF 和 10μF 电容器对 AVDD 和 DVDD 电源进行去耦;它们应尽可能靠近设备放置。

硬件和软件

AD7799/ADuC847电子秤参考设计也可以使用RS-232接口连接到任何PC。这允许用户在评估系统时保存和处理数据。

审核编辑：郭婷