积分器和采样保持器中单极和两级运放环路带宽分析

前言

积分器和采样保持器(S/H)是数模混合集成电路中一个关键的模块，常被用来进行信号采样或积分。为了保持采样/积分的精度，积分器和采样保持器中运放需要在规定的时间内充分地建立，通常这个过程分为大信号建立和小信号建立两个过程，前者用运放的压摆率(Slew Rata,SR)衡量，后者和运放的闭环带宽BW，也可以说是时间常数()息息相关。因此，SR和BW是评价积分器或采样保持电路中运放的关键指标和设计考量。

本文分别对应用单级运放和两级运放两种情况下的积分器或S/H在积分/保持相位的带宽进行了简单的分析，以此为设计者在设计积分器/采样保持电路时设计运放提供参考。不足之处请读者指正。

积分器和S/H环路带宽分析

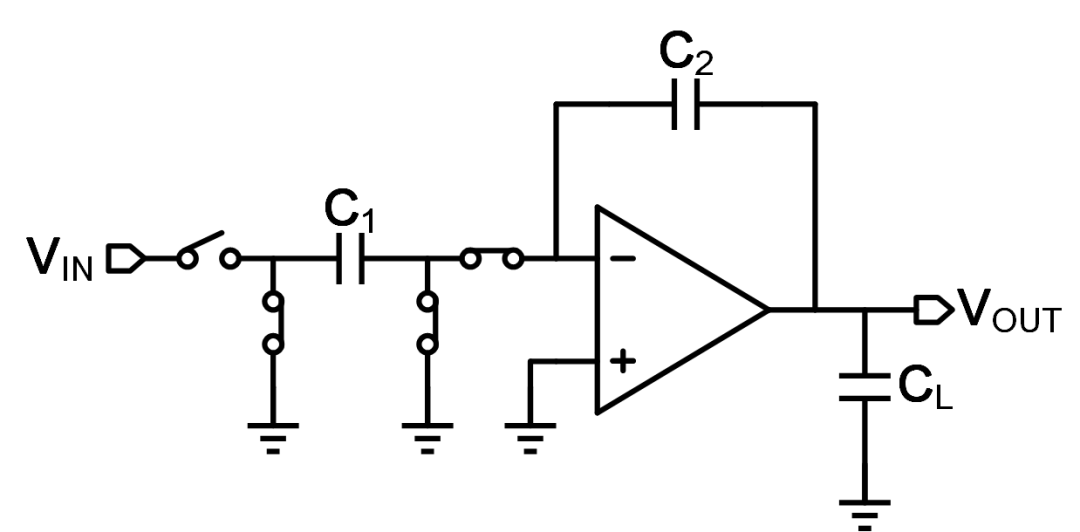
图1 积分器和S/H电路积分/保持相电路

积分器和S/H电路工作在积分或保持状态下电路如图1所示（为简化采用单端电路展示）。在该相位，由于闭环运放的虚短虚断特性，电容C1上的电荷全部转移至电容C2上。如果作为采样保持电路，则在采样相时通过额外的开关(图1未给出)对C2上的电荷清零，那么那保持相电荷完全转移后，得到输出为：V OUT =V IN *(C 1 /C 2 )。

如果作为积分器，那么第n个积分周期电荷完全转移后得到的输出为：V OUT [n]=V OUT [n-1]+V IN *(C 1 /C 2 )。

上述的过程并不是在开关切换之后就立即完成的，而是一个过程，其时间由运放的带宽（输入信号大时还存在大信号压摆过程）决定的。因为运放为了保持稳定性，一般为一个单极点系统，因此上述建立过程其实就是一个一阶RC小信号建立，运放的闭环带宽即反应建立的时间常数。因此，研究运放在该环路中的闭环带宽是探究建立时间或建立精度的重要过程。

单级运放积分器和S/H闭环带宽分析

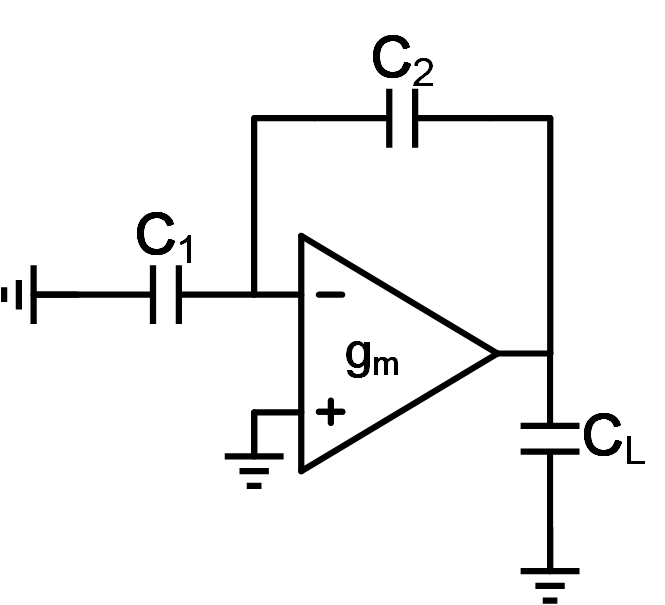
图2 单级运放积分器或S/H电路积分/保持相小信号模型

采用单级运放的积分器或S/H在积分或保持相的小信号如图2所示。要计算带宽，我们需要明确三个量：* 运放跨导gm

• 环路的反馈系数β
• 运放的等效负载电容Cequ

首先跨导gm即为运放的自身跨导值。

其次，反馈系数由电容C1和C2分压产生，其值为β=C 2 /(C 1 +C 2 )。

最后也是最重要的是等效负载电容。运放的输出负载电容由两部分组成：1) 积分器或S/H的负载电容C L ，通常这个电容为后面所衔接电路的输入电容；2) C1和C2组成的等效电容，由于运放的输入为虚断点，因此该等效电容即为C1和C2两个电容的串联值。运放的输出等效电容Cequ因此可以被表示为式(1)：

在计算闭环带宽时，本文提供如下两种思路：

思路1

首先根据运放跨导和等效负载电容计算出运放的单位增益带宽积GBW，如式(2)所示:

由于闭环增益为1/β，因此闭环带宽可通过GBW除以闭环增益1/β得到，如式(3)所示：

得到带宽后，时间常数即为1/BW，如式(4)所示：

思路2

闭环运放的输出阻抗可以表示为式(5)：

闭环运放的时间常数为Rout与Cequ的乘积，因此可被表示为式(6):

带宽即为时间常数的倒数。

上述两种方式在本质上是一样的，不过是两种不同的理解方式，而两者计算所得值也是相同的。

根据上述过程我们得到了积分或S/H电路在积分或保持相的闭环带宽和时间常数公式，在设计时我们可以通过该公式对自己设计的电路能否在时钟所给的时间内充分建立进行评估。

两级运放积分器和S/H闭环带宽分析

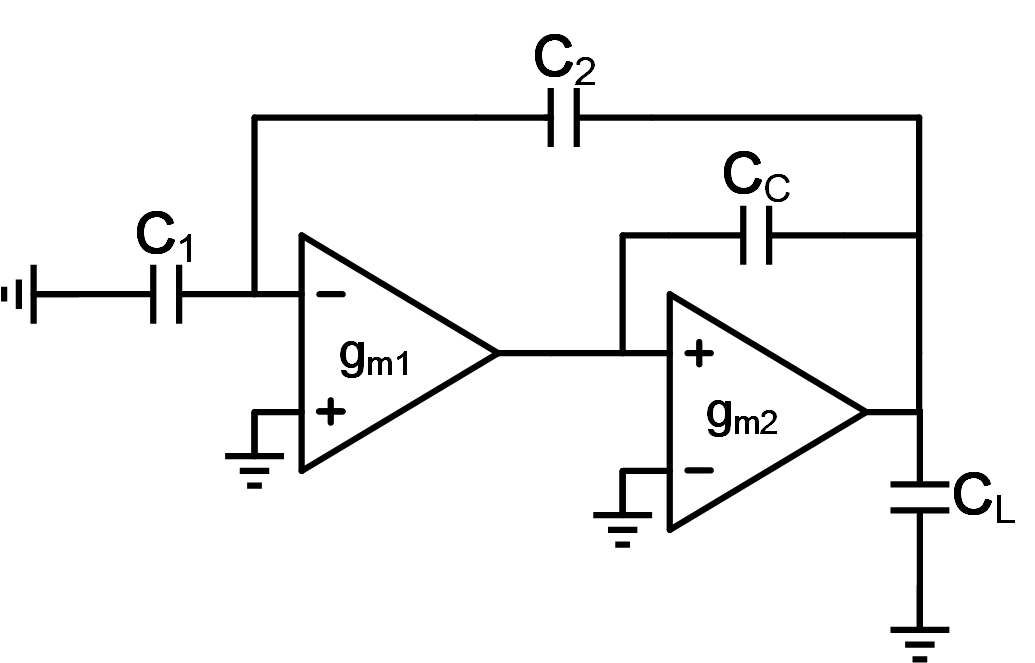
图3 两级运放积分器或S/H电路积分/保持相小信号模型

相比单级运放，两级运放的情况会更复杂一些，主要的原因为其包含两个极点。如图3所示，两个极点分别为第一级运放的输出和第二级运放的输出。通常我们在设计两级运放时，为了保证其具有足够的相位裕度，会通过密勒补偿将两个极点进行分裂，最终第一级运放输出形成的极点在补偿后成为主极点。计算两级运放组成的积分器或S/H电路的闭环带宽，按照我们在计算单级运放情况时采用的思路2，则需要我们计算形成闭环后的主极点大小，也就是计算主极点处的电阻（或电导）和电容值。主极点处的闭环点电导值为式(7)：

该公式的由来可以解释如下：

• 假如在第一级输出添加一个电压V，则该电压传到第二级输出值为gm2r out2 *V；
• 经过反馈路径传到第一级输入值为：βgm2r out2 *V；
• 之后在第一级输出产生的电流值大小为：βgm1gm2r out2 *V；

综上，第一级输出的跨导值为：βgm1gm2r out2 。上述rout2为第二级运放的小信号输出电阻（图3中省略）。

根据密勒效应，主极点处电容值为式(8)：

因此，运放闭环带宽表示为式(9):

运放闭环时间常数即为闭环带宽的倒数。

单级运放和两级运放情况下对比

式(9)中，我们可以明显地看出闭环的带宽为GBW-g m1 /CC与反馈系数β之积，而在单级运放中也是这样的，这也符合我们在拉扎维等书本上所学习的知识。但是，单级运放和两级运放还是存在区别，单级运放的带宽受负载电容C L ，采样电容C 1 ，积分电容或保持电容C2直接影响，而两级运放似乎不受这三个电容的影响（在反馈系数不变时），其只受到弥勒补偿电容CC的影响。造成这样结果的原因是两级运放本身在设计时便将第二级输出定为非主极点，其在保持相位裕度充足时，是不会影响带宽的。

在电路设计时，由两者区别可以得到一个启示：如果采用两级运放，电路中采样电容，积分或保持电容，负载电容改变只能通过影响反馈系数来影响闭环带宽和时间常数，如果只是改变了电容的绝对值而不改变反馈系数，那么时间常数就不需要重新仿真或者计算了。然后，如果采用单级运放，每一个电容的每一次更改都有可能影响到闭环带宽和时间常数，可能都需要重新仿真和计算。

总结

本文分别分析了采用单级和两级运放的积分器或采样保持电路的闭环带宽和时间常数计算方法，对比了两者的共同和不同之处，为读者在考虑积分器或采样保持电路能否充分建立时提供一些参考。不足之处请多多指正！