基于Opamp构建一个Wien桥式振荡器电路

　　振荡器电路是产生指定频率的特定波形的电路。当任何指定应用需要信号源时，这些电路会派上用场。在这里，我使用Opamp构建了一个原始的Wien桥式振荡器，该振荡器的尺寸最小，可为您的电路提供完美的信号源。

　　维也纳桥振荡器电路：

　　

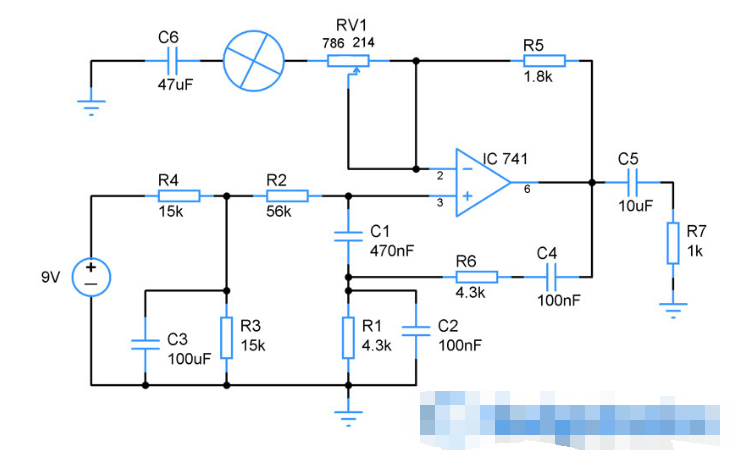
　　电路工作原理：

　　这是一个维也纳桥式振荡器。基本上，它只是一个具有一个正反馈（串联和并联RC网络）和一个负反馈（1.8k电阻，电位计和白炽灯泡）的放大器。其背后的想法是，串联/并联RC网络的精确信号衰减为3倍（-6dB）。这是因为两个网络以相同的频率共振，但一个是低通滤波器，另一个是高通滤波器。每个滤波器在中心频率处具有-3dB。当组合时，衰减变为-6dB。

　　为了使其工作，放大器必须具有3（6dB）的精确增益。在低于 3 的任何振荡都不会开始，而在高于 3

的任何振荡时，振荡将上升到截止失真。无论您多么努力，由于半导体的热漂移和电源轨的变化等原因，您永远无法将增益设置为正好3。惠普意识到，你可以用灯泡来稳定振幅。这是因为白炽灯泡具有正热系数（PTC）。这意味着当空闲时，它的电阻很低，当电流开始通过它时，它的电阻会增加。

　　让我们追溯振荡器中的过程。使用电位计，您可以将增益设置为略高于3。振荡开始上升，这通常会导致切断，更多的电流开始流过灯泡。随着电流的增加，灯泡的电阻也会增加。这导致负反馈增强，将增益降低到3以下。所以输出开始逐渐消失。随着它的减少，流过灯泡的电流越来越少，它的电阻也开始下降。这导致负反馈减弱，随后增益高于3。所以输出开始上升。这个循环一直持续到达到平衡状态并且输出稳定为止。

　　这种方法的几个优点是，由于灯泡的时间常数（Tau）比振荡低得多，它引起的失真远低于任何其他类型的稳定。这是因为其他类型的试图在波的每个周期中强制执行校正，在每个波中引入失真。这种方法在低得多的时间常数（几赫兹）下强制校正，因为灯丝需要时间来加热和再次冷却。另一个明显的优势是在很宽的电源电压范围内具有稳定性。

　　缺点之一是，如果您想要各种各样的频率，则需要在电路中采取一些预防措施，否则您需要重新调整负反馈以获得最佳失真。

　　输出波形：

　　

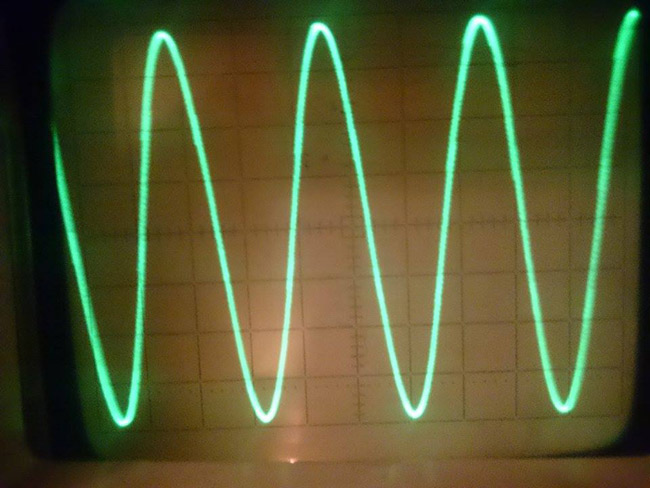
　　注意：

　　使用的运算放大器是IC 741。

　　您可以使用在圣诞树或任何其他装饰灯中找到的小灯