

对非线性系统的分析
描述
实际上的系统都是非线性的。
但是对非线性系统的分析,比对线性系统的分析,要复杂。
所以,在一些特定的条件下,就假设系统是线性的,比如说当输入信号很小的时候,我们可以假设放大器是线性的。
but,非线性其实一直都存在的。
比如说,对于一个RF接收机,当只有微小的小信号的时候,我们可以把他近似为线性系统。
但是如果有大的干扰信号进来,它就会有非线性行为。
一个无记忆的非线性系统,可以用下式表示。所谓无记忆系统,是指其输出,主要取决于当前的输入x(t),而和以前的输入无关。
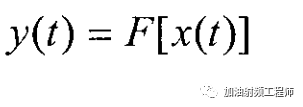
然后,将上式中的右边展开为一个幂级数,如下图所示。
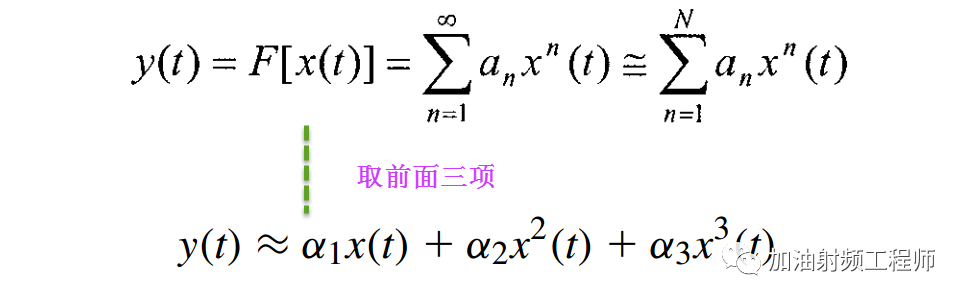
假设输入信号x(t)中包括三部分,分别为:
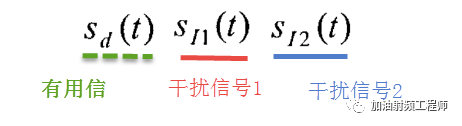
于是,非线性系统的输入y(t)为:
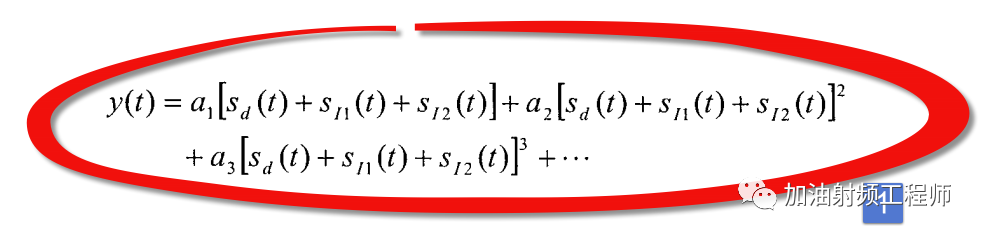
就是从这个式子,可以让我们观察到多种不同的非线性响应。
情况1:
增益压缩和Desensitization
增益压缩呢,就是指当有用信号功率增大时,系统的增益会呈现压缩的现象。
Desensitization,也是一种增益压缩,只不过是因为干扰信号的功率增大,导致系统的增益出现压缩,从而使得有用信号的增益下降,出现阻塞的现象。
假设有用信号为单音信号,频率为f0;干扰信号也为单音信号,频率为f1;另一个干扰信号为0,如下图所示。
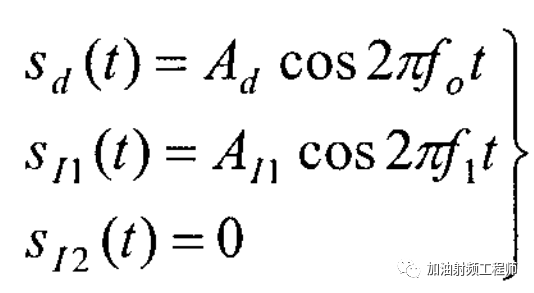
代入上式(1),可以得到:
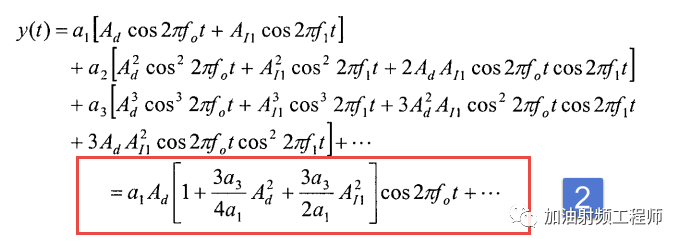
现在来对式2进行较为深度的剖析。
case1:
当干扰信号没有,且有用信号的幅度很小(Ad<<1)时,上式(2)可以简化为:
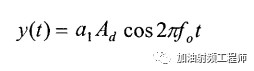
因此,此时系统的小信号增益为a1,这时的系统,近似为一个线性系统。
case2:
有用信号的幅度开始变大(干扰信号还是假设没有),此时系统的增益开始随着信号功率的变化而变化。
式2中括号里的第二项:

变得不能忽略。
如果a3的符号与a1的相反,那么随着信号功率的增加,系统增益变小。
这种现象称为增益压缩(gain compression).
此时,增益大小如下式所示。
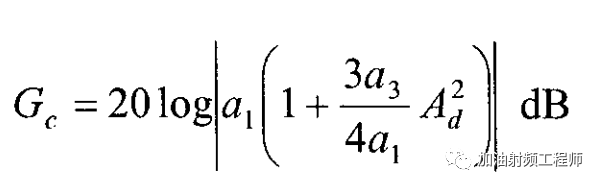
当增益比小信号增益下降1dB时,此时的输入功率,被称为输入1dB压缩点。
因此可以得到:
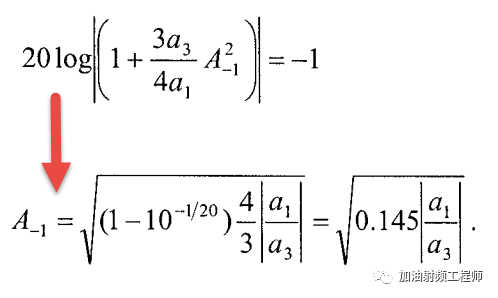
case3:
现在考虑上干扰信号,当a3<0时,如果干扰信号的幅度升高,系统的增益也会下降。
从式2中可知,干扰信号导致增益下降的幅度为:
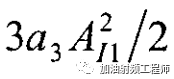
这种非线性现象,称为desensitization.
所以,当干扰足够强的时候,可能会导致系统的增益下降到0,此时有用信号的增益就是0,那么有用信号将会被完全阻塞。
情况2:
交调(crossmodulation)
如果输入信号x(t)包括一个小幅度的有用单音信号和一个强干扰信号,且该强干扰信号上有幅度调制,即:
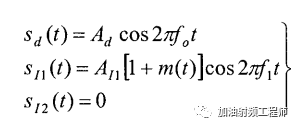
该非线性系统的输出变为:
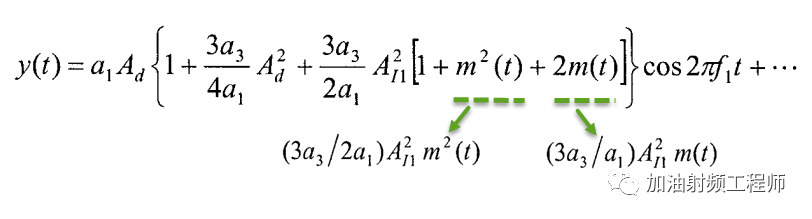
可见,除了desensitization和增益压缩项外,还有两个新增的项。
这些新的项,则表示强干扰信号上的幅度调制,由于系统的非线性特性,被转移到有用信号上了。
这种非线性现象称为交调(crossmodulation).
情况3:
互调(intermodulation)
现在考虑输入信号x(t)中,除了有用信号外,还有两个干扰信号,并假设他们都是单音信号,即:
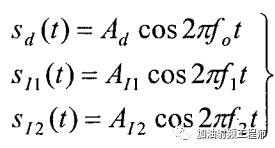
所以,可以得到:

在上式中,频率(f1±f2)的项,称为二阶互调产物;频率(2f1±f2)和(2f2±f1)的项为三阶互调产物。
这种非线性现象称为互调(intermodulation).
审核编辑:刘清
-
浅析非线性系统的相平面法2023-06-30 7027
-
线性系统的时域分析资料分享2021-06-30 1141
-
何长安非线性系统控制理论的PDF电子书免费下载2020-03-28 2143
-
自动控制系统教程之非线性系统分析的资料免费下载2020-01-10 1330
-
非线性系统描述函数法2016-05-31 1993
-
非线性系统辨识模糊模型参数收敛问题研究2011-08-19 895
-
非线性系统控制及解耦2011-05-11 886
-
非线性系统辨识2009-12-22 790
-
一种典型的非线性系统分析2009-08-29 1269
-
非线性系统输出反馈控制2009-08-13 624
-
基于正交小波网络的非线性系统辨识2009-06-24 537
-
基于多模型的非线性系统广义预测控制2009-06-17 723
全部0条评论

快来发表一下你的评论吧 !

