基于几何的泰森多边形来生成形体骨架

  世界各地的雨量分布存在着巨大的差异，即使是方圆百米内也可能出现东边日出西边雨的情况。那么科学家们是如何根据气象站的降雨数据计算各个地区的平均降雨量的呢？让我们一起来了解在计算平均降雨量中运用到的泰森多边形吧！     1911年，荷兰气候学家Thiessen根据离散分布的气象站的降雨量，提出了一种计算平均降雨量的方法，即将所有相邻气象站连成三角形，作这些三角形各边的垂直平分线，于是每个气象站周围的若干垂直平分线便围成一个多边形。应用这些多边形对气象观测站进行有效区域划分，多边形内所包含的一个唯一气象站的降雨强度来表示这个多边形区域内的降雨强度，这个多边形便被称为泰森多边形（Thiessen Polygon），泰森多边形也叫Voronoi图，或dirichlet图（下图中虚线构成的多边形就是泰森多边形，其每个顶点是每个三角形的外接圆圆心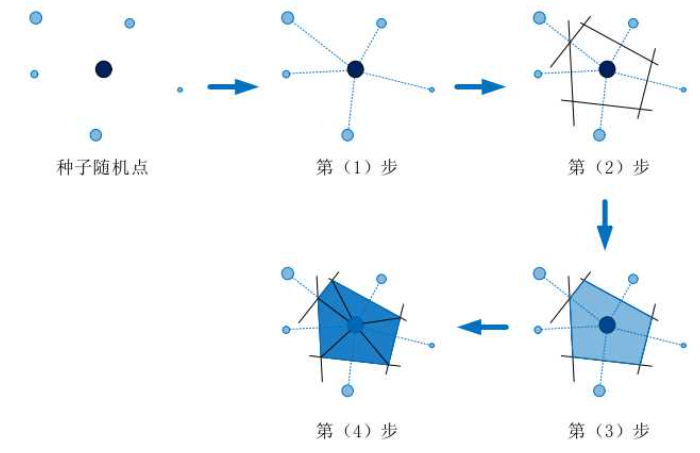）。   泰森多边形生成原理   上面我们提到的是基于制图算法生成Voronoi的方法，还有另外一种方法则是基于图形算法生成Voronoi的方法，即以离散点为圆心画圆，随着半径的逐渐增大，相邻的圆形会逐渐融合，直至生成最终的Voronoi。   基于制图算法生成Voronoi的方法 基于图形算法生成Voronoi的方法   泰森多边形最早由俄国数学家Georgy Fedoseevich Voronoi提出，它是关于空间邻近关系的一种算法。作为一种分隔空间的方式，在几何学、计算机图形、图像处理与模式识别、物理、化学、地理学、气象学以及机械制造等许多领域有广泛的应用。根据以上对泰森多边形的描述我们可以知道它具有以下性质：

高效性：每个泰森多边形内仅含有一个离散点；

泰森多边形内的点到相应离散点的距离最近；

位于泰森多边形边上的点到其两边的离散点的距离相等。

  因此，泰森多边形多用于定性分析、统计分析、邻近分析等。例如，可以用离散点的性质来描述泰森多边形区域的性质；可用离散点的数据来计算泰森多边形区域的数据；判断一个离散点与其它哪些离散点相邻时，可根据泰森多边形直接得出，且若泰森多边形是n边形，则就与n个离散点相邻；当某一数据点落入某一泰森多边形中时，它与相应的离散点最邻近，无需计算距离。  
 


在自然界中，泰森多边形的身影是随处可见的，如干涸的土地、长颈鹿的肌理、蜻蜓的翅膀、叶脉的形态等，再比如著名的建筑水立方。  
 

  生态学中常用泰森多边形法来确定空间实体的影响范围，如城市的影响范围及竞争分析。Brown在1965年最早把泰森多边形法用于树木竞争分析，提出潜在生长空间，利用树木为离散点所生成泰森多边形的面积来表示目标树可利用生存空间的大小；在图像处理领域，泰森多边形的应用之一是生成形体的骨架，许多研究采用基于几何的泰森多边形来生成形体骨架，从而把骨架作为形体的抽象表示。  
        责任编辑：彭菁利用