网络存储系统容错编码技术进展

 

　　1 存储容错编码评价指标

　　近20年来，随着计算机技术的迅猛发展，大规模存储系统的发展也十分迅速。当前，普通PC机的存储器的容量已经达到了太比特级别，这较之20年前的20 MB存储容量提高了10 000倍。

　　除了传统的磁盘驱动器之外，新型的固态存储(SSD)存储器也已经走向市场。尽管单个存储器的容量发展迅速，但是却仍然赶不上人们对存储容量需求的增长速度。

　　随着大型计算机系统由“以计算为中心”向着“以信息处理为中心”的转变，以及信息量的爆炸式增长，人们对海量存储系统的需求日益提高。海量存储系统本质上是将很多的单个存储器件(下面均以磁盘为例)，通过系统的接口，连接整合为一个虚拟的容量巨大的单一存储器，即磁盘阵列。

　　随着阵列中磁盘数目的增多，系统的可靠性也随之下降。工业界一般使用平均数据丢失时间(MTTDL)来衡量阵列的可靠性。

　　设单个磁盘的平均失效时间为MTTFdisk，则对于包含n块磁盘的无冗余阵列来说，其MTTDL可简单估计为：MTTDL=MTTFdisk/n。可见，当n较大时，整个系统的可靠性将成比例下降。这对于较大规模的系统来说是不可接受的。利用冗余数据编码来提高系统可靠性是公认的解决这一问题的较好方法。通过巧妙地将m块标准大小的磁盘上的数据，增加部分冗余校验信息，编码后存放于n块磁盘上，使得系统满足：对于任意k块磁盘失效，都可以通过其他n-k块未失效盘中的数据解码恢复，则称整个系统是k容错的，或者称k为系统的容错数。

　　分析表明[1]，对于k容错的系统来说，可以近似估计为：

　　

 

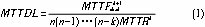
　　因而，在大规模系统中，容错数可以说是另一种对系统可靠性的描述方式。市场中一般磁盘的MTTFdisk为105左右，系统修复时间MTTR一般为10左右。根据(1)式可以看出，当系统磁盘数为103～104时，一般2容错或是3容错编码就基本上可以满足存储系统的容错要求。

　　系统用于增加容错能力而添加的冗余越多，系统的额外造价也将越高。因而在具有相同容错数的前提下，人们往往追求更小的冗余度，即(n-m)/n的值，其中n为系统磁盘数、m为存储用户数据的磁盘数。根据编码理论的Singleton界，k容错系统的最小冗余度为：k/n。达到这一最小值的编码方法称做MDS码。目前多数存储编码研究都集中于构造不同参数下的MDS码。

　　除了上述指标，任何计算机系统的速度与效率永远是需要考量的重要指标。这里我们不讨论如何有效地并行处理多磁盘中的数据读取(那是另外一个较大的课题)，而着重研究由于冗余编码带来的额外计算开销。对于即便是相同的编码方法，由于编/解码算法的不同，可能计算效率的差异较大。由于在计算机系统中，最终的编码运算都会反映为一些二进制运算，因而研究者通常使用编码需要的总的二进制异或运算次数来衡量由于额外冗余编码带来的系统计算开销。对于一个随机存取的存储系统来说，随机小块信息写操作的性能尤为重要。编码运算中每个单元所参与的平均异或次数可以用来衡量这一指标，我们称其为编码的更新复杂度。

　　综合上面讨论，存储系统容错编码问题可以归结为寻求对如下指标进行优化的编码方法

　　系统满足需要的容错性能，容错数为k的系统。

　　系统有较小(或最优)的冗余度

　　系统有较小(或最优)的编码/更新复杂度。

　　2 线性编码

　　对于单容错系统来说，简单的奇偶校验即可使得上面的3个指标达到最优。经典的系统都是使用的这种方法。然而对于k大于1的情况，问题的解决就不是那么简单了。从通信编码理论的丰富成果中，两种比较有代表性的编码方法被人们挑选出来，并用于解决存储容错问题，他们是二进制线性码和RS码。

　　2.1 多维阵列码

　　图1所示是二维阵列编码及校验矩阵。二维阵列码是奇偶校验的自然推广，由图1很容易看出它是双容错的。二维阵列码保持了单容错时奇偶校验码的最优编码复杂度的特性，但是二维阵列码的冗余度不再是最优的了。

　　

 

　　二维阵列码也很容易推广为k维阵列。并且容易得到这样编码的k容错特性。但是随着k的增大，冗余会越来越大[2-3]。

　　2.2 Full码

　　图2所示是FULL-2码。FULL-2码可看做是二维阵列码的推广。

　　

 

　　FULL码依然保持了最优的编码复杂度，并且冗余度要比阵列码好很多。然而不幸的是，当k大于3时，FULL-k码不再是k容错的[4]。

　　2.3 RS码

　　图3所示是RS码的校验矩阵。RS码从最佳的冗余特性出发。达到Singleton界的RS码被人们提出并广泛应用。

　　

 

　　校验矩阵通过线性变换可以化为系统矩阵，用存储系统的语言亦可显式地区分出系统中哪些单元用于存储校验单元。可以看出，矩阵中的元素不再是“0”、“1”，而为有限域元素的幂，故编码需要使用有限域运算。在计算机系统中，有限域元素最后还是会被映射为“0”、“1”单元。这时每个有限域元素一般会被映射为多个“0”、“1”单元，而有限域运算也可以被分解为这些“0”、“1”单元的复杂运算。我们仍然以编码所需的异或运算为基本单位，则编码所需的异或运算次数和编码算法的巧妙程度有关。目前较好的域运算算法所需的异或次数大约为O(n3)[5]，计算复杂度相当高。RS码是MDS码，故冗余度是最优的。

　　3 阵列编码

　　上述几种编码各有优缺点，那么是否存在对于多指标同时最优的k容错编码方法呢?自文献[5]提出EVENODD码起，一大类只使用异或运算的阵列编码被提出并被人们广泛研究。

　　多维阵列或FULL码等二进制线性码每块磁盘只取一个逻辑单元进行校验运算。而阵列码则在每块磁盘上取多个逻辑单元，一起交叉进行校验运算。校验计算同2进制线性码一样，只使用二进制异或运算，但冗余度却可以与RS码相同。

　　3.1 EVENODD码

　　EVENODD码的想法很简单，每块磁盘中取若干单元，排成方阵，然后将这些单元分成不同的校验组，另外添加两块磁盘用于存储校验单元。所有校验组均使用简单的二进制奇偶校验。

　　水平校验与对角校验如表1所示。表1中D代表用户数据单元，P代表冗余校验单元。可以看出，Disk1—Disk5存储用户数据单元;Disk6、7存储冗余校验单元。Disk6的各单元为用户数据各行的水平校验和，而Disk7的各单元为用户数据的辅对角线校验和。

　　

 

　　设存储用户数据盘的数目为p(如上例中p=5)，则系统包含p+2块磁盘，前p+1块磁盘中的最后一个单元为虚拟0元，故每盘实际包含p-1个单元，最后一块磁盘包含p个单元。可以证明，当p为素数时系统是双容错的。

　　简单计算可知此时的系统的冗余度为(2p-1)/((p+2)(p-1)+1)。由于最后的校验盘多出一个单元，所以冗余度稍稍大于最优的2/(p+2)。为了达到最优值，文献[5]中使用如下技巧：将多出的单元(即辅对角交验和)叠加到该盘其他单元上，构造MDS的EVENODD码如表2所示。

　　

 

　　表2也可表示为如表3所示。

　　

 

　　也就是说当第一辅对角校验和为1时，其他各对角校验为奇校验;当第一辅对角校验和为0时，其他各对角校验为偶校验。这就是它被命名为EVENODD码的原因。

　　3.2 RDP码

　　从表2可以看出，为了得到冗余最优，EVENODD码的辅对角线上的单元的更新复杂度很高。每次更新这些单元的数据时都要同时更新其他p个校验单元。对于双容错编码来说，最优值为2。文献[6]中构造的RDP编码将这些单元的更新复杂度均衡到每个单元，从而有效地消除了写操作中更新性能的不均衡。一个包含水平校验的对角线校验如表4所示。

　　

 

　　与EVENODD不同处在于，做对角校验时也包含了水平校验单元的一列(因此，数据单元也比EVENODD少了一列)。

　　同样的，RDP的最后一个校验盘多出一个单元，使得整个系统不为MDS码。但RDP码的优势在于，简单地将多出的单元删去，系统仍然为双容错的。即得到如表5所示阵列。

　　

 

　　从表5可以看出，所有数据单元的更新负载为2或3，分布比EVENODD码要均匀，不会产生由编码方式带来的额外“瓶颈”，但系统的平均更新复杂度是相同的。

　　3.3 Liberation码

　　从前面几种编码可以看出，所使用的方法都是水平校验加其他一种校验共同构成双容错。不同之处就在于“另一种校验”的不同选择。如将另一校验盘上的校验元看作一个“0”、“1”向量，每块数据盘上的单元对这些校验元的影响可用一个“0”、“1”矩阵来表示。如表5中的第1列的4个数据单元对Disk7中的各校验元的影响可表示为如图4所示矩阵。

　　

 

　　在这种表示下，前面所说的更新复杂度就对应着矩阵中1的个数。于是构造一个双容错阵列码的问题就转变为：寻找若干个这样的矩阵，使得其中1的个数尽量少，并且任意2个之和为满秩。

　　在p为素数时，文献[7]中构造的Liberation码使得p×p阶矩阵1的数目不超过p+1，其构造的p个矩阵可简单地描述为：各对角线加一个额外单元。第k个矩阵的额外的1单元的位置可描述为(k(p-1)/2 Mod p,1+k(p=1)/2 Mod p)。得到的编码如表6所示。

　　

 

　　3.4 PDHLatin码

　　前面这些编码为MDS码的充要条件均为：码长与素数相关(RDP为p+1，其他为p+2)。它们的双容错解码方法均为根据一个已知单元，然后通过校验关系与失效单元形成的链式关系依次恢复所有单元。这使人们理解到其容错能力的本质是任意两列都可以形成这样的关联结构。文献[8]中利用拉丁方构造了PDHLatin码，使得码长不再必须关联一个素数。

　　所谓拉丁方是指n×n的方阵中填入n个不同符号，使得每行每列的符号都不重复。显然拉丁方的每两列构成一个n元置换。所谓汉密尔顿拉丁方是指拉丁方的任何两列构成的置换为单环的。图5为一个9阶汉密尔顿拉丁方。

　　

 

　　从一个给定的汉密尔顿拉丁方，我们可以用与EVENODD码类似的方法构造编码，只不过各单元对于第二校验盘的校验关系不再依单元所在对角线位置决定，而是根据拉丁方相应位置的符号决定。根据图5，得到表7所示的PDHLatin码。

　　

 

　　3.5 X码

　　上面介绍的几种编码方法虽然都达到了冗余的最优，但在更新复杂度方面均稍高于最优值，那么是否可以达到两者同时最优呢?文献[9]提出的X码是一种这样的双容错编码。

　　X码的想法也很简单，仍然是在阵列中采用主对角线和辅对角线两种校验，但是通过巧妙地将校验单元分布到各个磁盘中(而不是像其他方法中，校验单元被分离出来，独立存放于校验盘)，使得系统同时达到了两方面指标同时最优。

　　为了满足双容错的要求，X码也要求阵列中包含的列数(或说码长)为素数。码长为素数p的X码中，每一列包含p-2个用户数据单元，2个冗余校验单元。

　　3.6 B码

　　是否还存在与X码相同特性的其他编码方案呢?显然将两个X码阵列重叠，系统仍然保持最优冗余与最优更新复杂度。

　　这样得到的新编码，在磁盘数目不变的情况下，每块盘需要关联的单元数目加倍。而在实际中，为了简化实现，我们实际上需要每块盘关联的单元数目尽量少。对于n块磁盘，在保持最优冗余与最优更新复杂度的条件下，每块盘最少需要多少个单元来关联校验呢?文献[10]提出的B码在双容错的情况下很好地解决了这一问题。

　　通过将编码构造等同于图论中的完全图完美-因子分解问题。并根据图论已有的结论，给出一种各方面性能均达到最优的编码。依据一个完全图的一种完美1因子分解方案，我们可以构造如表8所示的双容错编码——B码。

　　

 

　　这种编码，每块磁盘包含至多1个校验单元，并且只有一块磁盘不包含校验单元。它将n个符号的所有2元组分划为多列，并且满足双容错要求，因而在保持了最优冗余度与更新复杂度的前提下，码长达到最长。因而这种编码也被称做最长最低密度阵列码。

　　3.7 T码

　　对于3容错的最长最低密度阵列码的构造较之双容错要复杂很多。文献[11]最先给出了一种这样的构造，并利用计算机辅助证明了某些参数下，3、4容错最长最低密度阵列码的MDS性。在文献[12]中独立构造了同样的编码并利用组合结构近乎可分的不完全区组设计(NRB)给出了这种编码的组合解释，同时也给出了简明的代数证明。

　　T码从形式上与B码相同，每块磁盘包含至多1个校验单元，并且只有一块磁盘不包含校验单元。文献[12]证明了对于任意容错的最长最低密度阵列码均满足这种性质。

　　对于普遍参数的T码，或任意容错的最长最低密度阵列码的构造，仍是困难问题。

　　3.8 Weaver码

　　前面的编码都将优化冗余率最优设为第一目标，同时兼顾编码/更新复杂度。但在一些系统中，如果冗余率的适当损失可换来更好的性能或更易于部署，则也是可选择的。文献[13]从优先考虑系统编码/更新复杂度的角度，提出了易于构造的Weaver码。

　　由B码、T码的构造也可以看出，在保持更新复杂度最优的前提下，校验单元分布在各磁盘中的编码比较容易构造。为了简化问题，文献[13]选择具有循环对称性的阵列进行研究。也就是说要求编码满足：(1)所有数据单元参与的校验组数为常数;(2)所有校验组包含的单元数目为常数;(3)如果磁盘i上的数据单元j参与磁盘k上的校验单元p所代表的校验组，则必有对于任何0≤x< mod n块盘上的数据单元j参与磁盘k+x>

　　为了更容易地得到k容错编码，文献[13]放宽了冗余的要求，只研究每块磁盘中，冗余校验单元不少于用户数据单元的情况。这样，Weaver码的最好冗余率只有50%。

　　4 结束语

　　阵列码尽管有着很多性能优势，但在目前的存储系统中，还是RS码及层叠RAID(如RAID1+0等)使用得比较多。笔者认为其原因主要为以下几个方面：

　　首先是实现上的简单性因素：RS码已经是工业界流行的技术，无论软硬件都有成熟的实现方案，而层叠RAID原理十分简单，所以这两种编码实施最简单易行。与之相对，阵列码多种多样、原理复杂，实施需要一定的投入。目前海量存储系统正处于发展阶段，什么是“最好的”编码尚不能形成定论，因而就目前阶段来讲，最简单的就是最好的。

　　其次，受到目前大部分应用的存储需求影响：尽管将多个单个部件合成一个统一的虚拟部件会有好处，但也会有相应的问题。如对10 000块磁盘是合成1个系统好呢?还是组成10每个包含1 000块磁盘的小系统好呢?这要根据需求来判断。一般来说小一些的系统会更容易管理和维护。目前只有极少的应用需要对超过1 000块盘容量的数据并行的处理，因而将系统分为多个较小系统是有益的。

　　第三，硬盘的造价较低且发展迅速：这使得人们可以比较“奢侈”地使用存储空间，因而大型存储系统的建造目前还处于“粗旷经营”阶段。相对于易实施性、易维护性、易扩展性，当前阶段冗余率还并不是主要决定因素。

　　但是，随着单磁盘容量的日趋饱和，系统对性能、容错、节能等需求的不断变化，海量存储系统构造相应的也会不断发展。明天的存储系统将会需要具备什么特性的编码形式，还需我们不断探索。