HDSR便携式调频串联谐振试验装置的工作原理

本篇将和大家讨论串联谐振的原理，并分析串联谐振现象的一些特征，探索串联谐振现象的一些基本规律，以便在应用中能更自如的使用串联谐振和分析在试验过程中发生的一些现象。

一、串联谐振的产生

谐振是由R、L、C元件组成的电路在一定条件下发生的一种特殊现象。首先，我们来分析R、L、C串联电路发生谐振的条件和谐振时电路的特性。图1所示R、L、C串联电路，在正弦电压U作用下，其复阻抗：

Z=R+jωL-1ωC=R+jXL-XC=R+jX

  

 

 

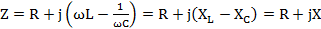
Χ(ω0)=ω0L-1ω0C=0 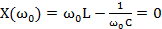  （式1）

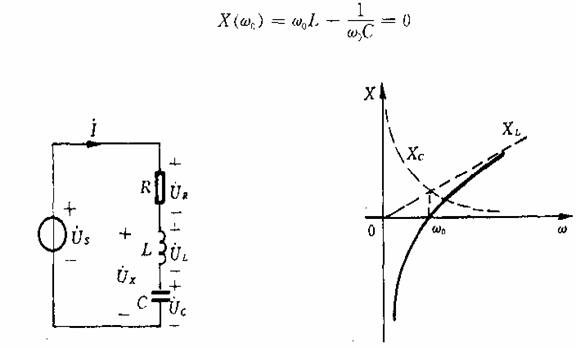
式中电抗X＝XL—Xc是角频率ω的函数，X随ω变化的情况如图2所示。当ω从零开始向∞变化时，X从﹣∞向﹢∞变化，在ω＜ω0时、X＜0，电路为容性；在ω＞ω0时，X＞0，电路为感性；在ω＝ω0时

图1                                          图2

此时电路阻抗Z(ω0)＝R为纯电阻。电压和电流同相，我们将电路此时的工作状态称为谐振。由于这种谐振发生在R、L、C串联电路中，所以又称为串联谐振。式1就是串联电路发生谐振的条件。由此式可求得谐振角频率ω0如下：

                ω0=1LC

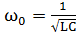
谐振频率为

                f0=12πLC

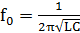
由此可知，串联电路的谐振频率是由电路自身参数L、C决定的．与外部条件无关，故又称电路的固有频率。当电源频率一定时，可以调节电路参数L或C，使电路固有频率与电源频率一致而发生谐振；在电路参数一定时，可以改变电源频率使之与电路固有频率一致而发生谐振。

图1                                          图2

此时电路阻抗Z(ω0)＝R为纯电阻。电压和电流同相，我们将电路此时的工作状态称为谐振。由于这种谐振发生在R、L、C串联电路中，所以又称为串联谐振。式1就是串联电路发生谐振的条件。由此式可求得谐振角频率ω0如下：

                ω0=1LC

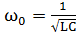
谐振频率为

                f0=12πLC

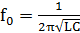
由此可知，串联电路的谐振频率是由电路自身参数L、C决定的．与外部条件无关，故又称电路的固有频率。当电源频率一定时，可以调节电路参数L或C，使电路固有频率与电源频率一致而发生谐振；在电路参数一定时，可以改变电源频率使之与电路固有频率一致而发生谐振。

 

二、串联谐振的品质因数

串联电路谐振时，其电抗X(ω0)＝0，所以电路的复阻抗

Zω0=R

  

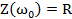
呈现为一个纯电阻，而且阻抗为最小值。谐振时，虽然电抗X＝XL—Xc=0，但感抗与容抗均不为零，只是二者相等。我们称谐振时的感抗或容抗为串联谐振电路的特性阻抗，记为ρ，即

ρ=ω0L=1ω0C=1LC∙L=LC

  

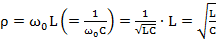
ρ的单位为欧姆，它是一个由电路参数L、C决定的量，与频率无关。

    工程上常用特性阻抗与电阻的比值来表征谐振电路的性能，并称此比值为串联电路的品质因数，用Q表示，即

Q=ρR=ω0LR=1ω0CR=1RLC

  

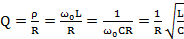
品质因数又称共振系数，有时简称为Q值。它是由电路参数R、L、C共同决定的一个无量纲的量。

三、串联谐振时的电压关系

谐振时各元件的电压分别为

URO=RIO=US

  

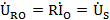
ULO=jω0LIO=jω0LUsR=jQUs

  

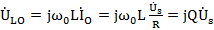
UCO=j1ω0CIo=-j1ω0CUSR=-jQUS

  

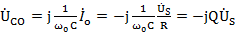
即谐振时电感电压和电容电压有效值相等，均为外施电压的Q倍，但电感电压超前外施电压90°，电容电压滞后外施电压90°，总的电抗电压为0。在电路Q值较高时，电感电压和电容电压的数值都将远大于外施电压的值，所以串联谐振又称电压谐振。

常见的试品如变压器、GIS系统、SF6断路器、电流互感器、电力电缆、套管等均为容性，系统配备的电抗器为感性，试验时先通过调节变频电源的输出频率使回路发生串联谐振，再在回路谐振的条件下调节变频电源输出电压使试品电压达到试验值。由于回路的谐振，变频电源较小的输出电压就可在试品上产生较高的试验电压。

在实际现场应用中试品上的高压电压和低压电压遵循以下公式：

U试 = QU激

其中：U试为高压谐振试验电压，Q为系统串联谐振的品质因数，      U激为激励变压器输出电压。

 例如：假设系统串联谐振的品质因数Q为30，激励变压器选择16kV的抽头，激励变压器额定输入电压为400V，如果激励变压器输入电压为100V时，高压电压计算步骤如下：

①计算激励变压器变比

激励变压器变比N=激励变压器所选抽头电压/输入额定电压

即：N=16kV/400V=16000/400=40

②计算激励变压器输出电压

激励变压器输出电压=激励变压器输入电压*激励变压器变比

即：U激=100V*40=4kV

③计算高压谐振试验电压

高压谐振试验电压=激励变压器输出电压*系统品质因数

即：U试=4kV*30=120kV

故系统最终的高压谐振试验电压为120kV。