【技术】FEC—数据防丢失，提升数据通信可信度！

 

 

前向纠错—FEC

前向纠错（FEC）是增加数据通信的可信度的方法。

 

前向的意义是纠错过程为单方向的，没有错误的信息反馈。利用数据进行传输冗余信息的方法，当传输中出现错误，将允许接收器再建数据。

 

即一种差错控制方式，信号在被送入传输信道之前会按一定的算法进行编码处理，加入带有信号本身特征的冗余码，在接收端按照相应算法对接收到的信号进行解码，从而找出在传输过程中产生的错误码并将其纠正。比较经典的编码解码方式例如汉明码、BCH码、RS码等。

 

汉明码（Hamming Code），是在电信领域的一种线性调试码，以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的消息流中插入验证码，当计算机存储或移动数据时，可能会产生数据位错误，以侦测并更正单一比特错误。

 

简单来说，前向纠错(FEC)就是在数据中添加冗余进行传输，检验出错误后通过冗余可以恢复原本的数据。汉明码是一种可用于前向纠错（FEC）的编码和解码方式。

 

一

奇偶校验

汉明码使用到了奇偶校验的方法，所以先复习一下——奇偶校验。

 

示例中高亮位为校验位，如果传输过程中，某一数据位发生错误，则检验便会不符合校验规则。

 

奇校验：所有传送的二进制代码的数位（含字符的各数位和校验位）中，“1”的个数为奇数。

 

例：1001 1011——0 1001 1011因传输的原始数据中，1的位数为5，奇数，所以校验位写0。

 

偶校验：所有传送的二进制代码的数位（含字符的各数位和校验位）中，“1”的个数为偶数。

 

例：1001 1011——1 1001 1011因传输的原始数据中，1的位数为5，奇数，所以校验位写1。

 

二

汉明码

1

什么是冗余

冗余，在汉明码中是附加在数据中的校验位，它是附加在数据的比特位之间，是一种二进制位，可以通过冗余位来检验数据错误和恢复正确的数据。那么，一个数据中的冗余位，应该是多少个，可以使用(式 2-1)计算：

2n >= m+n+1   (式 2-1)

(n:冗余位位数。m:数据位数。)

例：传输一个8位的数据0x9B，二进制表示为1001 1011，则计算n的结果为4：24>=8+4+1。

 

2

怎么分组

如下图2-1，假设有一个7位的数据，每个位编号1，2......7。分为3组：C1，C2和C3。

C1：1，2，4，5

C2：2，3，5，6

C3：4，5，6，7

 

始终假设，只有一个错误存在其中。

如果，只有C1区错误，C2和C3区没有错误，根据这个条件，可以看出，C2中2，3，5，6是没有错误的，C3中4，5，6，7没有错误，说明出错的是1。再来一次，如果C2和C3区有错误，C1区没有错误，这次我们可以排除C1中1，2，4，5没有错误，C2和C3只有一个错误，则出错的肯定是6。

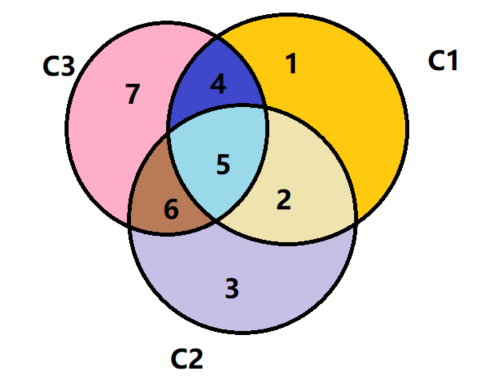
（图 2-1）

3

编码

接下来，我们开始编码了，使用奇校验方式，还是上面那个数字为例：0x9B，二进制表示位1001 1011，这是一个8位的数据，所以冗余位的个数位4，总的数据位数为12。

 

到这里，又出现了一个问题，冗余码放哪些位置呢？前面or后面？都不是，冗余码（奇偶校验码）穿插在数据中放置，放置的位置和冗余码数量有关，即位置在：20，21，22，23，24……2n-1。

 

示例为4个冗余位，则放置在第1，2，4，8位的位置上，如下图2-2，剩下的数据位，我们顺序填入需要编码的数据，如下图2-3。

（图 2-2）

（图 2-3）

 

这时候，我们发现了，图中我们不仅对数据位编号，并且表示为二进制，原因就是，数据位编号的二进制表示，是我们进行数据位分组的依据。接下来，我们开始分组：

①二进制编号第一位为1的：1，3，5，7，9，11    ————20

②二进制编号第二位为1的：2，3，6，7，10，11    ————21

③二进制编号第三位为1的：4，5，6，7，12        ————22

④二进制编号第四位为1的：8，9，10，11，12    ————23

 

高亮的编号位是每组对应填入奇偶检验位的位置，对实际的数据位数采用奇校验：

①组：1的个数为4，因此20处填入1

②组：1的个数为2，因此21处填入1

③组：1的个数为3，因此22处填入0

④组：1的个数为2，因此23处填入1

综上，编码后的数据为1001 1101 0111，如图2-4所示。

（图 2-4）

 

4

检错与纠错

数据传输过程中，如果没有错误，校验通过，则皆大欢喜。如果数据出错了呢，我们便要进行检错（找到错误）和纠错（纠正错误）。在此之前，我们还是要重复一下，汉明码最多只能纠错一个比特位的数据错误。我们接下来开始。

 

假设数据位编号为7的数据，在传输过程中，不小心，从”1“变成了”0”。如图2-5。

（图 2-5）

 

检错：

①奇校验第一组：目前数据位11，9，7，5，3，1数据表示为010111，此时数据位中1的个数为4，不满足奇校验，说明这一组数据中某一个位出错。因为要满足奇校验，所以需要补1满足。

（图 2-6）

 

②奇校验第二组：目前数据位11，10，7，6，3，2数据表示为000011，但是此时数据位中1的个数为2，不满足奇校验，说明这一组数据中某一个位出错。因为要满足奇校验，所以需要补1满足。

（图 2-7）

 

③奇校验第三组：目前数据位12，7，6，5，4数据表示为10010，但是此时数据位中1的个数为2，不满足奇校验，说明这一组数据中某一个位出错。因为要满足奇校验，所以需要补1满足。

（图 2-8）

 

④奇校验第四组：目前数据位12，11，10，9，8数据表示为10011，此时数据位中1的个数为1，满足奇校验，说明这 一组数据正确。只需要补0。

（图 2-9）

 

纠错：

重新校验之后，把补上的数位按照从高位到低位排列得出：0111，也就是7。所以，错误的数位编号为7，只需要将收到的数据的第七位取反，即得到正确的发送方发送的数据：1001 1101 0111。