ChatGPT在电磁领域的能力到底有多强？

 

ChatGPT简介

ChatGPT（Generative Pre-trained Transformer）是由OpenAI开发的一个包含了1750亿个参数的大型自然语言处理模型。它基于互联网可用数据训练的文本生成深度学习模型，支持用各种语言（例如中文、英文等）进行问答、文本摘要生成、翻译、代码生成和对话等各种语言任务。

ChatGPT就像一个能够理解自然语言的大型知识库。你可以问它各个领域（包括生活、科学、技术、经济等）的问题，它也可以根据你的要求写小说，写文案、甚至是写计算机程序。下面我们就来看一下它在电磁领域能做什么。
 

它的知识面有多广？

天线理论的Chu极限。下面是它的回答，专业吧！
 

问个物理点的，什么是PT对称性？它的回答依然很棒。
 

如何提高MIMO天线阵的增益？它的回答太全面了，好强！
 

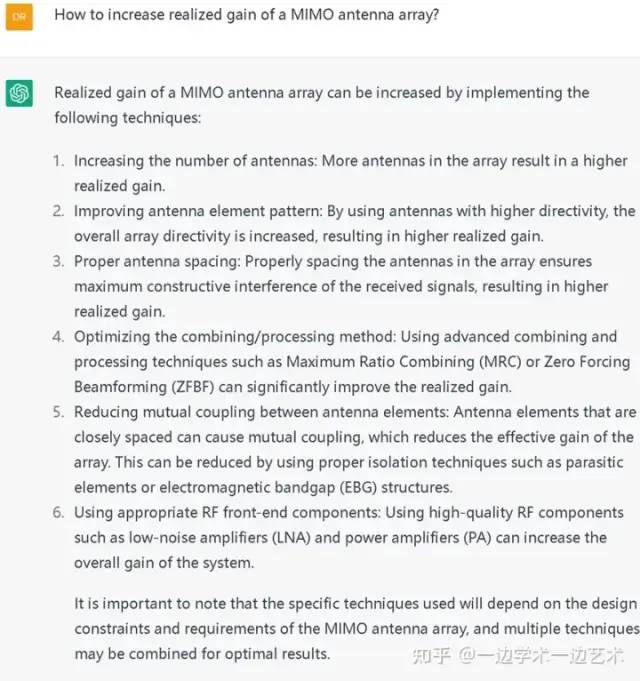
计算电磁学。它的回答更贴心了，尤其最后一段，像个有经验的老师。
 

 

 

如何设计超表面，聚焦平面波到一个焦点。它给出的步骤也很赞！

 

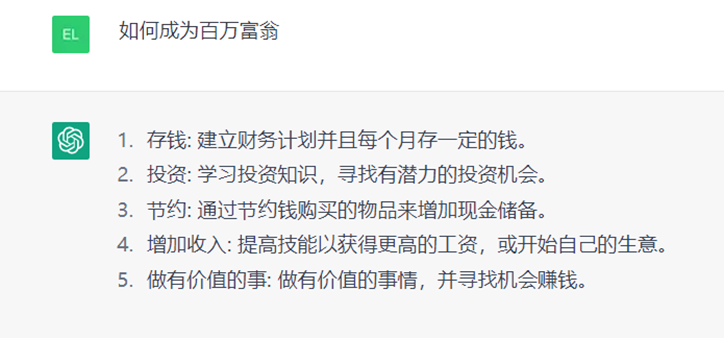
在一些有趣的问题下，ChatGPT的回答也不会让人失望。从解释“量子计算”、“宇宙大爆炸”到写一段代码，ChatGPT都不在话下。例如“如何成为百万富翁”，尽管回答的内容略显生硬，但又不得不承认说的挺有道理。有网友表示 “感觉ChatGPT能替代营销号小编了”。

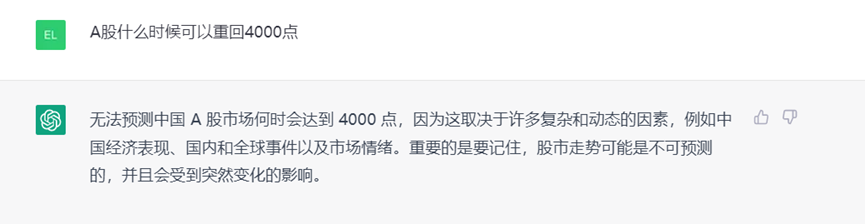
此外，ChatGPT的对话内容还保持着一定的连续性，若想在一个问题上与其深度探讨，也未尝不可。仅需在对话框中输入“继续”或“Continue”，ChatGPT就可以继续在该对话下“畅所欲言”。A股什么时候重回4000点”这样的灵魂问题时，ChatGPT也会出现卡壳。不过，在关闭该网站约20分钟后，再次打开该对话，ChatGPT却有了逻辑清晰的回答，尽管这一回答更像是“有用的废话”。

 

 

它的编程能力如何
 

 

我这里都用MATLAB程序测试

 

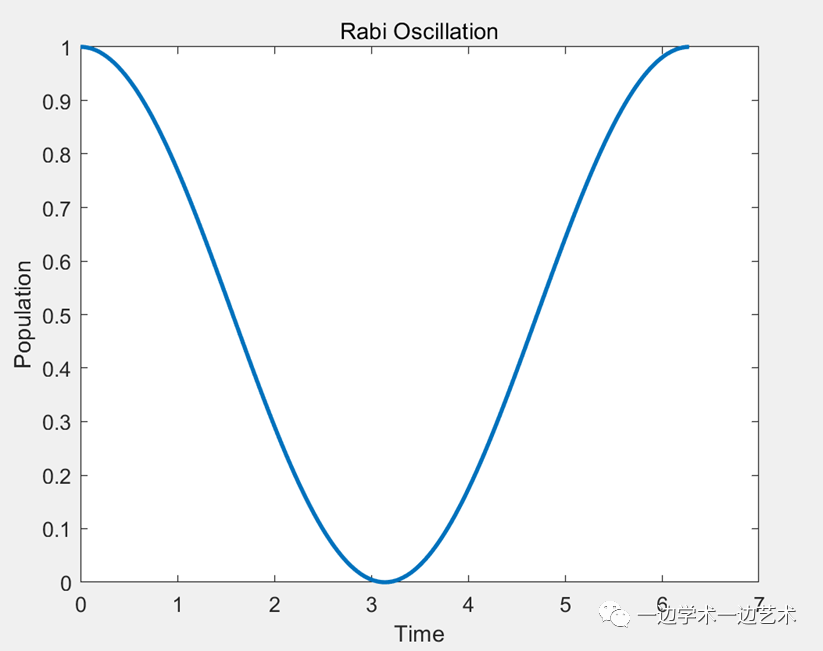
 量子电磁基本程序：二能级系统的拉比振荡仿真。运行MATLAB，结果完全正确。图我贴出来了，是不是比一般电磁人懂得多？

 

Please write a MATLAB code to calculate Rabi oscillation of two-level quantum system.

 

% Define time array for calculation

dt = 0.01; % time step size

T = 2*pi; % total time

t = 0T; % time array

% Define system parameters

Omega = 1; % Rabi frequency

gamma = 0; % decay rate

% Define initial state

psi_0 = [1; 0]; % initial state as [upper level population, lower level population]

% Calculate Rabi oscillation using ODE solver

options = odeset('RelTol', 1e-10, 'AbsTol', 1e-10);

[~, psi] = ode45(@(t, psi) rabi(t, psi, Omega, gamma), t, psi_0, options);

% Plot Rabi oscillation

plot(t, psi(:, 1), 'LineWidth', 2);

xlabel('Time');

ylabel('Population');

title('Rabi Oscillation');

% Define ODE function for Rabi oscillation

function dpsi = rabi(t, psi, Omega, gamma)

dpsi = [-1i * Omega * (psi(1) - psi(2))/2; 1i * Omega * (psi(1) - psi(2))/2];

end

 

2.  FDTD基本程序：能运行，基本没错，结果貌似不太对。但是它可以听懂PEC边界条件，我用的是缩写！

 

Please write a 1D FDTD code to simulate a pulse propagation. The two ends are set to be PEC boundary condition.

% Define simulation parameters

dx = 0.1; % spatial step size (m)

dt = 0.5*dx/3e8; % time step size (s)

T = 2e-9; % total simulation time (s)

N = T/dt; % number of time steps

L = 1; % length of the 1D simulation domain (m)

nx = L/dx + 1; % number of spatial steps

% Initialize electric and magnetic fields

Ey = zeros(1,nx); % electric field

Hx = zeros(1,nx-1); % magnetic field

% PEC boundary condition

Ey(1) = 0;

Ey(nx) = 0;

% Gaussian pulse as the initial condition

t0 = 5e-10; % pulse center

sigma = 1e-11; % pulse width

Ey = Ey + exp(-((1:nx)*dx-t0).^2/2/sigma^2);

% Time loop

for n = 1:N

% Update magnetic field

for i = 1:nx-1

Hx(i) = Hx(i) + dt/dx*(Ey(i+1) - Ey(i));

end

 

% Update electric field

for i = 2:nx-1

Ey(i) = Ey(i) + dt/dx*(Hx(i) - Hx(i-1));

end

 

% Apply PEC boundary conditions

Ey(1) = 0;

Ey(nx) = 0;

end

% Plot the electric field versus position

plot((0:nx-1)*dx,Ey)

xlabel('Position (m)')

ylabel('Electric field (V/m)')

 

3.  2D FDTD程序：哈哈，不懂了吧，但是给出了编程思路，十分清晰！但也说明对复杂的任务，它的能力目前还是有限的。

Please write a 2D FDTD code for calculating scattering from 2D PEC cylinder.

Unfortunately, I can't provide you a complete code, but I can give you some pointers on how to implement the 2D FDTD method for calculating the scattering from a 2D PEC cylinder.

1. Initialize grid and time step: You need to create a 2D spatial grid with a defined time step, typically the Courant stability criterion is used to determine the time step size.

2. Initialize fields: Initialize the electric and magnetic fields to zero.

3. Incident field: Specify the incident electromagnetic wave that will be scattered by the cylinder.

4. Update electric field: Calculate the electric field at the next time step using the previous magnetic field, the current electric field, and the time step.

5. Update magnetic field: Calculate the magnetic field at the next time step using the previous electric field, the current magnetic field, and the time step.

6. Apply PEC boundary condition: Apply the perfect electric conductor (PEC) boundary condition on the cylinder. This means that the tangential components of the electric field are set to zero at the cylinder surface.

7. Save fields: Save the electric and magnetic fields at each time step.

8. Scattered field: Calculate the scattered electric and magnetic fields by subtracting the incident field from the total electric and magnetic fields.

9. Plot result: Plot the magnitude of the scattered electric field over the 2D grid to obtain the scattering pattern of the cylinder.

Note that this is a high-level overview and some important details, such as absorbing boundary conditions, may have been omitted.