一种广角镜头成像几何畸变校正算法实现

摘要 ：由于成像光学系统固有的特性，以及镜头成像平面与物体平面存在的倾斜角和转角，使得获取的图像存在着非线形几何畸变。在对图像进行定量分析和检测之前，必须消除这些畸变。为此，本文提出了一种以校正径向几何畸变为主的非线性校正方法。讨论了控制点的选取原则，建立了三次多项式的畸变校正模型；分析了不同灰度重建方法的特点，进行了仿真实验，校正结果良好，在成像测量应用中有很好的实用价值。

在用光学镜头摄像机采集图像时，由于物面与像面的不平行投影、镜头畸变和摄像机质量等因素的影响，其采集的图像存在着几何畸变。尤其是现在广泛用于监视系统的短焦距，广角镜头系统，畸变较为明显，在进行基于图像分析的运动检测、模式匹配等定量分析时，就需要对这类系统的畸变进行校正，以产生精确的低失真的图像。

镜头的几何畸变有径向和切向两类，通常径向畸变比切向畸变大的多，因此，在一般的工作中主要考虑径向畸变，而忽略切向畸变。径向畸变主要是由镜头的径向曲率不同造成的，有枕形和桶形畸变两种。研究表明，在一般情况下，对广角镜头的成像，只要采用三次多项式变形技术和双线性插值法，就可消除这类失真，得到理想的图像。其中，采用多项式拟合进行空间坐标变换是关键性的一步。

1 几何畸变校正的原理

在几何畸变图像校正中常用一幅基准图像去校正畸变图像，设基准图像的坐标为(u，v)、畸变图像坐标为(x，y)，重采样成图法采用的二维多项式数学模型为

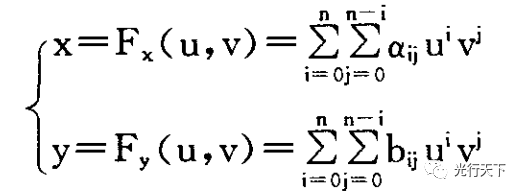
 （1）

式中：n为多项式的项数，aij和bij为各项系数。

设基准图像为g(u，v)，而畸变图像为f(x，y)，对于图像中的同一个点，假设其灰度值是不变的，即

g(u，v)=f(x，y) （2）

式(2)为图像几何畸变校正的基本公式。基准图像中的X、Y为整数，而由式(1)计算得到的X、Y不一定为整数，必须进行灰度插值运算。

2 灰度插值方法比较

常用的插值方法有最邻近点法、双线性内插法及三次卷积法三种。

a. 最邻近点法

最邻近点法的实质是取原始畸变图像4个邻近点中距离坐标(x，y)最近的点(x'，y')的灰度作为该点的灰度，即g(u，v)一f(x'，y')

其 中 ：x'=IFIX(x+0.5)；y'=IFIX(y+0.5)。

最邻近点法的优点是算法非常简单并且保持原光谱信息不变；缺点是几何精度较差，使校正后的图像不具有连续性，表现为原来光滑的边界出现锯齿状。

b. 双线性内插法

双线性插值法利用4个邻近点的灰度在两个方向上作线性插值。具体算法为

设点(u，v)落在(x，y)、(X+1，y)、(x，y+1)和(x+1，y+1)之间，则复原点(u，v)上的灰度值为：

g(u，v)=(1一α)(1一β)f(x，y)+α(1一β)f(x+1，y)+(1一α)βf(x，y+1)+αβf(x+1，y+1) (3)

式中α=u-x，β=v-y。

双线性插值法具有计算简单、几何上准确度较高、能克服灰度不连续等优点，缺点是由于亮度内插，图像的光谱信息发生了变化，易造成高频成分的损失，使图像变的模糊。

c. 三次卷积法

三次卷积法是利用一个一元三次多项式来近似理论上的最佳重采样函数

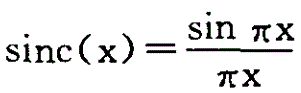
，相当于在(x，y)周围的4*4邻域内进行二维重采样，由于参与运算的点数多造成计算量较大，优点是不仅图像的亮度连续以及几何上比较精确，而且还能较好地保留高频成分。

综合考虑计算速度和精度的要求，本文采用了双线性内插法进行畸变校正。

3 控制点(GCP)的选取

多项式(1)中的各待定系数可以利用K个控制点坐标按最小二乘法原理来求得，即使最小二乘误差

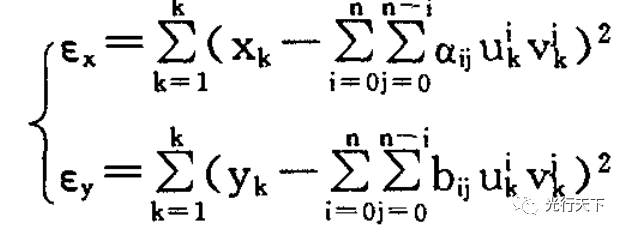
 （4）

为最小。由于多项式项数N与其阶数n有着固定的关系，即N=(n+1)(n+2)/2

因此，根据控制点数据用最小二乘法来计算未知系数时，控制点的数目必须不小于N个。在本文中采用了三次多项式，至少需要选择1O个控制点。另外在选择控制点时要注意控制点的分布，为了输出图像的精确，应使控制点分布均匀，在靠近图像的边界和四角顶点的地方要保证有控制点，以保证输入畸变图像和输出校正图像大小相等。

4 图像畸变校正过程

在实际的光电测量系统中获得了如图l所示的畸变图像，物方原来的直线成像后变成了曲线，显然要得到实际物体正确的线度信息，必须对此非线性畸变进行修正。畸变校正可以按以下三个步骤进行：

(1)建立原始畸变图像与校正后图像的坐标系。确立校正图像的原点，图像大小(行数和列数)等。

(2)根据上述中控制点的选取原则在原始畸变图像与标准空间中确定控制点。

(3)选择畸变数学模型，由于原始图像是复杂的非线性畸变(见图1)，为得到较好的输出图像至少要选择三次多项式校正(tk数越高图像的拟合越精确，但是也会带来计算量的巨增)，然后利用上一步骤中获得的控制点数据，确定多项式的未知参数，并分别根据最邻近点法和双线性内插法对畸变图像进行灰度重建。

5 仿真实验及分析

实验条件：

(1)摄像头，PH380型，镜头焦距f=3.5mm的CCD摄像头。

(2)成像数据采集器320*240(pixe1)。

(3)样本图样为8*8的正方形网格测试图。

采用三次多项式畸变校正技术以后得到的实验结果：

图2所示为采用最邻近插值法复原的图像。

图3所示为采用双线性内插法得到的图像。

从实验结果看，无论采用最邻近插值还是双线性内插方法都对因镜头不完善所致的畸变得到明显的校正，并且也验证前面所述的采用双线性内插法复原的图像相比最邻近法采样精度和几何上更为精确，图像亮度连续，避免了出现图2中的锯齿状线条边缘。

本文的方法是一种比较便捷的几何畸变校正方法，只要样本图做的好，并使样本图尽量垂直于光轴，则会使本方法更有效。从实验结果中，我们也注意到，校正后像的边缘有极小部分像点无图像信息，这是因采用反向映射法计算时，在边缘处的坐标超出了实际畸变图像的坐标范围，无可用象素点所致，但在实际畸变图像的每点都已获校正，故不影响像的校正结果。

　　审核编辑：汤梓红