

雷达方程与RF链路分析
电子说
描述
雷达方程大家一直是既熟悉又陌生的状态,熟悉在于其形式之简,无非就是几个物理量的乘除,物理模型及概念又清楚明了;陌生在于虽其形式之简,但使用起来终究有种食之无味,弃之可惜之感,之后就束之高阁了。原因在于,雷达方程本质是一个将环境电磁传播,目标散射属性,雷达射频硬件,信号处理算法等紧密联系起来的方程式。换句话说,雷达方程是一个将物理组件实体和软件信号虚体紧密联系的伟大方程。
方程同时涉及硬件,射频天线及软件算法。负责硬件的同学,可能熟悉PCB特性,比如怎么样的板材的介电常数比较稳定,损耗较小,从而实现高质量电磁辐射。负责射频天线的,对天线增益,阻抗匹配,传输线损耗比较熟悉。做软件算法的,对信噪比估计,FFT算法等比较擅长。但是,这三位同学如果只是限于自身领域,是不可能对雷达方程有更深层次认识的,始终会处于似懂非懂的境地,用起来也就味同嚼蜡了。
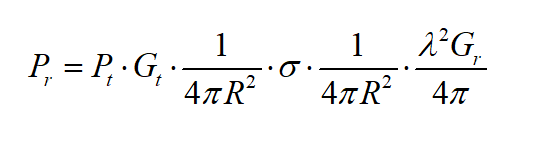
▲ radar equation
事实上,深入了解雷达方程并不需要硬件,射频天线及软件算法方面的艰深知识,只要这三个领域一些基本的知识概念即可,我尝试抛砖引玉,分享一种我的理解思路及分析逻辑。并且我也会分享关于雷达方程在工程中的作用以及使用注意点等。
需要说明,关于雷达方程模型解释方面的资料多如牛毛,考虑篇幅以及文章定位,不再赘述,读者可以自行查阅其他资料,这样做虽使得文章略欠系统性,但我希望主要把雷达方程最本质的东西呈现于你。
另外指出,雷达方程常用的还有对数形式,对于单发单收(SISO),方程如下,

▲ radar equation(log type)
我以一个具体的例子贯穿全文阐述雷达方程,并且联系实际。
大家可能看过TI radar chip的datasheet,比如AWR1642(如下图)

▲ 器件概述(局部)
其中蓝框内有个重要的参数指标RX噪声系数(Noise Figure,NF),在76-77GHz内可以做到14dB。噪声系数如何定义以及计算大家可以自行查阅资料。这个参数极为重要,并且越小越好。那么TI设计为14dB是否有什么依据,或者说TI将噪声系数设置为14dB有什么思考逻辑,又或者说这个数值是不是芯片性能与成本的某种平衡。我尝试从雷达方程的角度提供一个解释,从中也可以反应雷达方程的作用以及加深你对雷达方程的认识。
TI公司设计的AWR1642,功能框图如下。
 ▲ AWR1642功能框图
▲ AWR1642功能框图
其中,RX接收共有4路,如功能框图图蓝框所示,每一路可以称为接收模拟链路(RX analog chain),该链路包含两大核心组件,RF(如LNA,mixer),以及baseband(如IF,VGA,HPF等),需要指出,前述的噪声系数并不是链路中某个器件的噪声系数,而是整个模拟接收链路(rx analog chain)的整体噪声系数。因此,噪声系数(NF)可以理解为,对应于每个channel,接收信号在LNA输入到ADC输入这个过程中的信噪比损失。
那么这个信噪比损失也就是噪声系数设置为多少合适呢,如果太小,当然是极好的,好是好估计要费好多钱和头发,成本扛不住。如果太大,算法中有用信号被噪声淹没了,雷达就废了。不过,借助雷达方程,我们可以粗略估计其数值。

▲ 雷达电磁传播
首先,在确定NF之前,我们暂时先回到天线设计,我们设计的天线必须达到足够的灵敏度(Sensitivity),所谓灵敏度就是雷达天线能够接收微弱信号的能力表征。这与功能需求有关,比如,要求载频77GHz雷达在80m处检测到一个成人(rcs=0dBsm),并且雷达的辐射功率为12dBm,收发天线增益为12dBi。忽略一些损耗,根据前述雷达对数方程,在接收端某个channel,LNA输入前的雷达接收信号能量为-121dBm(Pr = rcs - R + Gt + Gr + Pt + K),这些量都是对数形式,K为方程中常数项的对数,所以Pr = 0 - 40*log10(80)+12 + 12 + 12 + 10 log10((0.00392.^2)/((4pi).^3)) =-121dBm。
假设rx端灵敏度足够高,能够检测接收-121dbm的信号功率,也就是说LNA端的输入是-121dBm,若不考虑通道增益不平衡以及环境杂波,每个channel的-121dBm能量将通过各自的rx analog chain 以及ADC处理。之后就是算法上距离维,速度维,角度维的处理。这个过程中,rx analog chain若干组件会放大接收信号,也就是接收信号获得增益,但同时也会引入噪声(通常是热噪声)。算法上的处理,如FFT处理同样引入信号处理增益。那上述这些增益及噪声与NF有何关联?继续分析。

▲ Receive Subsystem (Per Channel)
信号目标判决通常在算法层实施,如在range-Doppler map 进行阈值判断以及CFAR处理从而确定有效检测,这里有个算法上的核心工作: 确定全局信噪比 。信噪比的确定方法有很多,不过不在本文讨论之列,假设我确定了该信噪比SNR为17dB,也就是说,任何低于17dB的目标检测都视作无效目标检测点。
将前述增益,噪声,NF,以及SNR这几个量统一的方式就是修正后的雷达方程。其对数形式为,

其中SNR中的Pr是在算法中做完距离维,多普勒维FFT后估计的接收功率。如果Pr是LNA前的接收信号功率,那么上式将修正为,

本文开头的雷达方程止于接收端LNA之前的信号分析。如果再考虑rx analog chain以及信号处理算法链路,并引入检测信噪比,那么雷达方程的形式将得到修正,也就是得到式(1)。
修正后的雷达方程非常有用。我们首先用它来估计NF。
比如接收端的检测信噪比为17dB,上式kTNF表征热噪声,在微波频率上,噪声通常是在接收机内部产生的。在接收机输入级的电阻部分会由于导电电子的热运动而产生噪声,称为“热噪声”或“约翰逊噪声”,k为玻耳兹曼常数,数值上等于1.38e-23。T为热力学温度。NF为噪声系数。NTr中N为chirp个数,Tr为chirp时宽。
那么若NTr为10ms,也就是累计时间为10ms,该数据代入方程(1)后得到,
NF = -40*log10(80)+12+12+12-81+174-20-17 = 15.8dB
通常,NTr要远大于10ms,对NF的要求更低。所以式中的数据相对苛刻些。至此我们完成了NF的合理估计。那么你可能还有疑惑,方程(1)如何来的?
事实上,式(1)的非对数形式为,

其中的NTr = NMTs,其中M为chirp采样点个数,Ts为快时间维采样间隔。所以,上式可以进一步得到,

其中P_algo是算法中估计信号功率,P_beforeADC是信号输入ADC之前的功率,P_LNA是LNA前测量的信号功率。由此可见,式(1)与本文开头的雷达方程也是统一的,只不过经过算法处理后需要补偿FFT的增益而已。
以上分析以及计算都是基于一定的前提条件,包括但不限于
1 收发天线无波束倾斜(no Antenna beam tilt measurement),也就是天线辐射boresight.必须对准0°。天线波束tilt与多种因素有关,比如PCB,天线与馈电设计,RF,壳体与天线罩。像一些高增益天线以及低成本PCB材料容易发生波束tilt,需要详细测试或校准。
2 无多通道天线增益不平衡以及无相位失配(mismatch),如果存在问题,需校准。
3 忽略PCB传导损耗(Conductor Loss),介电常数变化,铜箔不平整等问题。
4 不考虑温度影响,否则需要温度校准。比如温度对相位的校准表。
5 环境路径损耗,天气引起的各类损耗,可以作为修正项引入。
事实上,式(1)的作用包括但不限于,
*TX-RX 回环SNR测量计算,并与RF链路理论分析结果对比,从而评估SNR合理性
*将TX输出功率以及RX端噪声系数整合,能够识别整个链路中发射端天线增益,输出功率,接收端天线增益可能存在的问题。
也就是说,如果你的雷达测距范围在算法上已经穷途末路,那不妨试试雷达方程链路分析手段,或许你会发现一些链路组件值得改进优化的点,从而进一步增强你的雷达测距性能。
-
ISM RF产品的无线链路计算2012-04-12 3421
-
怎么简化RF信号链路的分析?2019-10-18 2686
-
用于Si4455 868 MHz RF收发器的EZRadio双向链路开发套件2020-05-22 2461
-
新手求助磁链定向中的重要控制方程有哪些?2021-06-30 1406
-
浅析磁链方程2021-09-06 2996
-
超宽带合成孔径雷达方程研究2016-12-28 1014
-
无人机的RF链路的设计指南2017-09-14 1121
-
RF MEMS技术的雷达系统的解析2017-11-07 1025
-
ISM RF产品的无线链路预算表2017-11-24 2347
-
采用NF可简化RF信号链路的研究分析2019-07-15 2784
-
雷达方程及其推导过程2023-08-23 3278
全部0条评论

快来发表一下你的评论吧 !

