

如何使用Python中的SciPy库计算系统的脉冲响应?
电子说
描述
引言:脉冲响应是信号处理和系统分析中的重要概念,它描述了系统对单位脉冲输入的响应。通过分析系统的脉冲响应,我们可以了解系统的时域特性、频域特性以及对不同输入信号的响应方式。本文将详细介绍脉冲响应的概念,并展示如何使用Python中的SciPy库计算系统的脉冲响应。
一、脉冲响应的概念
脉冲响应是指系统对单位脉冲信号的响应。单位脉冲信号是一个在时刻t=0处取值为1,其余时刻取值为0的信号。脉冲响应可以描述系统对任意输入信号的响应情况,因为任意信号都可以看作是单位脉冲信号的线性组合。通过观察脉冲响应,我们可以了解系统的时域特性,包括系统的延迟、振荡、衰减等。
二、脉冲响应的计算
在Python中,我们可以使用SciPy库来计算系统的脉冲响应。SciPy库提供了信号处理模块(scipy.signal),其中包含了用于系统分析和信号处理的函数和工具。
以下是使用SciPy库计算系统脉冲响应的基本步骤:
(1)定义系统的差分方程表示或传递函数表示。差分方程表示描述了系统的输入输出关系,传递函数表示则描述了系统的频率响应特性。
(2)使用scipy.signal中的函数将差分方程或传递函数转换为系统的脉冲响应。常用的函数包括impulse和impulse2函数。
(3)可选:绘制脉冲响应的图形以进行可视化和分析。
下面是一个示例代码,演示了如何使用SciPy库计算系统的脉冲响应:
from scipy import signal
import matplotlib.pyplot as plt
# 定义系统的差分方程表示
b = [1, 2, 1] # 分子多项式的系数
a = [1, -1, 0.5] # 分母多项式的系数
# 使用scipy.signal中的impulse函数计算系统的脉冲响应
t, y = signal.impulse((b, a))
# 绘制脉冲响应的图形
plt.stem(t, y)
plt.xlabel('Time')
plt.ylabel('Amplitude')
plt.title('Impulse Response')
plt.grid(True)
plt.show()
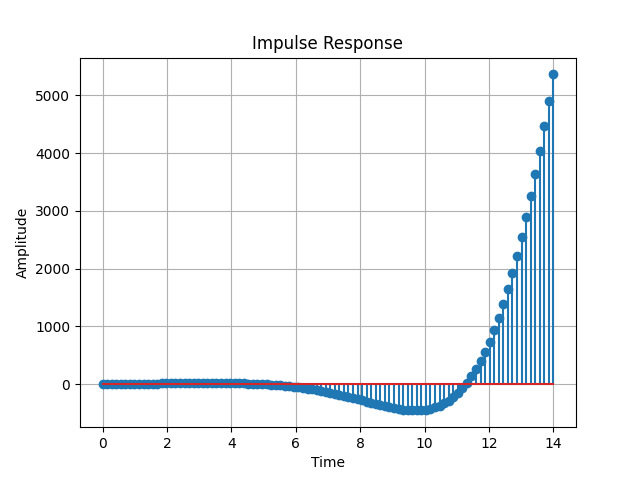
通过上述代码,我们首先定义了系统的差分方程表示,其中b和a分别是分子多项式和分母多项式的系数。然后,使用signal.impulse函数计算系统的脉冲响应,该函数接受差分方程的系数作为输入,并返回脉冲响应的时间和幅度数组。最后,使用Matplotlib库绘制了脉冲响应的图形。
signal.impulse函数是SciPy库中用于计算系统脉冲响应的函数,它的输入参数和输出如下所示:
输入参数:
sys:表示系统的差分方程或传递函数。可以通过传递一个包含分子多项式和分母多项式系数的元组 (b, a) 或传递一个 scipy.signal.TransferFunction 对象来表示系统。分子多项式的系数为 b,分母多项式的系数为 a。
T:表示时间的数组。可以通过传递一个一维数组来指定时间的取样点。如果未指定,则函数会自动计算一个合适的时间范围。
输出:
tout:表示输出的时间数组,即脉冲响应的时间轴。
yout:表示输出的幅度数组,即脉冲响应的幅度。
通过调用 signal.impulse 函数并传递适当的参数,可以获得系统的脉冲响应的时间和幅度数组。
三、脉冲响应的分析
通过计算系统的脉冲响应并可视化,我们可以进行进一步的分析和理解。
1.脉冲响应的幅度:观察脉冲响应图形中的幅度变化。幅度表示系统对单位脉冲的放大或衰减程度。通过观察幅度的变化,我们可以了解系统的增益特性和衰减特性。
2.脉冲响应的时延:观察脉冲响应图形中的时延。时延表示系统对输入信号的延迟时间。通过观察时延的大小,我们可以了解系统的延迟特性。
3.脉冲响应的形态:观察脉冲响应图形中的形态和波动。形态和波动可以提供关于系统的振荡、阻尼和共振等特性的信息。通过分析脉冲响应,我们可以深入了解系统的时域特性和频域特性,包括系统的稳定性、频率响应和相位响应等。这有助于我们理解系统的行为,进行系统设计和优化,并在信号处理和控制系统等领域中应用脉冲响应分析的知识。
-
自动控制原理的一阶系统的单位脉冲响应曲线的初始斜率怎样计算是对的2017-02-20 5727
-
在 MaxCompute UDF 中运行 Scipy2018-05-17 2588
-
PNA-X脉冲响应中的颠簸2018-11-15 1265
-
响应与脉冲响应的预期振荡行为不匹配2019-07-05 899
-
请问怎么用滤波器实现滤除单位脉冲响应的某些频率部分2019-11-09 3338
-
模拟低通滤波器和数字有限脉冲响应滤波器有何不同2021-07-29 2408
-
ADA4961脉冲响应异常怎么解决?2023-11-14 790
-
数字信号处理实验指导 -无限长单位脉冲响应(IIR)滤波器的2009-05-10 986
-
相关函数脉冲响应法系统实时辨识_邓春龙2017-03-15 908
-
了解数据科学Python库2017-11-15 4241
-
TL431脉冲响应时间测试2017-12-12 7828
-
用于Python的英特尔,加速NUMPY和SCIPY技术2018-10-15 6131
-
数字信号处理教程之有限脉冲响应滤波的详细课件免费下载2019-11-13 1232
-
基于脉冲响应函数的波走时研究分析综述2021-04-25 938
-
Scipy是什么?Scipy子模块有哪些呢?2023-08-09 3563
全部0条评论

快来发表一下你的评论吧 !

