零极点分析的基本原理、应用和意义

在信号处理和系统理论领域，零极点分析是一项重要的技术，用于研究和分析滤波器的特性和行为。通过观察滤波器的零点和极点在复平面上的分布情况，我们可以揭示滤波器的频率响应、稳定性和传输特性等关键信息。本文将深入探讨零极点分析的原理、应用和意义，带您一起揭开滤波器特性的奥秘。

一、零极点分析的基本原理

在深入了解零极点分析之前，我们首先需要了解什么是零点和极点。在滤波器的传递函数中，零点是使得传递函数为零的频率值，而极点则是使得传递函数无穷大的频率值。通过将传递函数表示为分子和分母多项式的比值，我们可以获得滤波器的零极点。

传递函数的分子多项式表示零点，而分母多项式表示极点。具体而言，分子多项式的根表示零点的位置，而分母多项式的根则表示极点的位置。通过观察这些根在复平面上的分布情况，我们可以了解滤波器的特性。

二、零极点分析的应用和意义

零极点分析在滤波器设计、频率响应评估和稳定性分析等方面具有广泛的应用。让我们来看看它们在实际中的应用和意义。

1. 频率响应评估 ：通过观察滤波器的零点和极点在复平面上的位置，我们可以推断滤波器对不同频率的信号的响应。具体而言，零点和极点的位置决定了滤波器在不同频率下的增益和相位响应。这对于了解滤波器的频率特性和选择合适的滤波器类型非常重要。

2. 稳定性分析 ：通过观察极点的位置，我们可以判断滤波器是否稳定。如果所有的极点都位于单位圆内部，那么滤波器是稳定的。反之，如果有极点位于单位圆外部，滤波器可能是不稳定的。稳定性是滤波器设计中必不可忽视的因素，因为稳定的滤波器可以确保系统的可靠性和预测性能。

3. 滤波器设计和优化 ：零极点分析在滤波器的设计和优化中发挥着关键作用。通过调整零点和极点的位置，我们可以控制滤波器的频率特性和响应。例如，通过移动零点和极点的位置，我们可以改变滤波器的截止频率、带宽和斜率等参数。这种灵活性使得零极点分析成为滤波器设计中的重要工具，可以满足不同应用的需求。

三、实例展示与实用工具

为了更好地理解和应用零极点分析，我们可以通过实例展示和实用工具来加深我们的认识。

例如，我们可以使用Python中的信号处理库来进行零极点分析。通过使用库中的函数，我们可以将滤波器的分子和分母多项式转换为零极点的表示形式。然后，我们可以利用这些信息绘制零极点图，直观地观察它们在复平面上的分布情况。这样的可视化工具可以帮助我们更好地理解滤波器的特性。

import matplotlib.pyplot as plt
import numpy as np
from scipy import signal
from matplotlib.patches import Circle



N = 8 # quantization bits
Fs = 1000 # sampling frequency
a = np.array([1, 1.7, 0.745]) # denominator
b = np.array([0.05, 0, 0]) # numerator
# z zero, p pole, k gain


z1, p1, k1 = signal.tf2zpk(b,a) # zero, pole and gain

c = np.vstack((a,b))
Max = (abs(c)).max() #find the largest value
a = a / Max #normalization
b = b / Max

Ra = (a * (2**((N-1)-1))).astype(int) # quantizan and truncate
Rb = (b * (2**((N-1)-1))).astype(int)
z2, p2, k2 = signal.tf2zpk(Rb,Ra)



fig, ax = plt.subplots()
circle = Circle(xy = (0.0, 0.0), radius = 1, alpha = 0.9, facecolor = 'white')
ax.add_patch(circle)
for i in p1:
  ax.plot(np.real(i),np.imag(i), 'bx') #pole before quantization
for i in z1:
 ax.plot(np.real(i),np.imag(i),'bo') #zero before quantization
for i in p2:
 ax.plot(np.real(i),np.imag(i), 'rx') #pole after quantization
for i in z2:
 ax.plot(np.real(i),np.imag(i),'ro') #zero after quantization

ax.set_xlim(-1.8,1.8)
ax.set_ylim(-1.2,1.2)
ax.grid()
ax.set_title("%d bit quantization" %N)
plt.show()

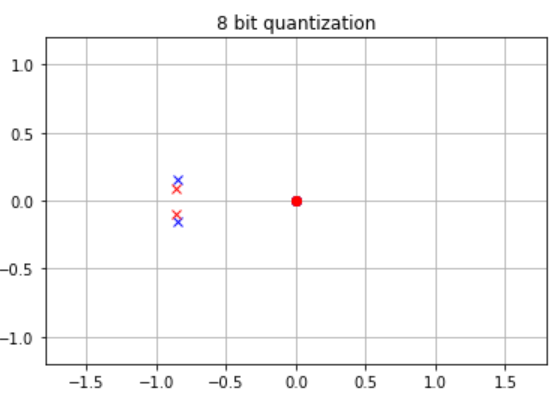
在分析零极点图时，可以通过以下几个步骤来观察和理解图形中的信息：

1.零点和极点的位置：观察图中的零点和极点在复平面上的位置分布。零点通常用圆圈表示，而极点通常用叉（如红色叉）表示。注意它们的位置相对于原点以及它们在实轴和虚轴上的分布情况。

2.零点和极点的数量：计算零点和极点的数量。它们的数量可能会对系统的特性和频率响应产生影响。例如，零点的数量决定了系统在不同频率上的增益变化，而极点的数量则决定了系统的阶数和稳定性。

3.零点和极点的相关性：观察零点和极点之间的相关性和互相之间的位置关系。例如，零点和极点是否成对出现，是否存在共轭对称的关系，以及它们的距离和角度关系。这些关系可以提供有关滤波器的相位响应、幅频特性和稳定性的信息。

4.零点和极点的对称性：检查零点和极点的对称性。如果零点和极点是共轭对称分布的，即它们成对出现并以实轴为对称轴，那么滤波器的频率响应将是实数值。这种对称性可以对设计无失真滤波器或频率选择性滤波器提供指导。

5.零点和极点的角度和频率响应：观察零点和极点的角度和频率响应。零点和极点的角度可以提供有关相位响应的信息，而频率响应可以反映滤波器在不同频率上的增益变化和特性。

通过观察和分析零极点图，我们可以获得有关滤波器特性、频率响应、相位响应和稳定性等方面的重要信息。这有助于我们理解系统的行为、设计滤波器和优化系统的性能。

signal.tf2zpk是scipy库中的一个函数，用于将连续时间或离散时间系统的传递函数表示转换为零点-极点-增益（ZPK）表示形式。该函数接受两个参数，分别为传递函数的分子和分母多项式的系数。

函数签名如下：

z, p, k = signal.tf2zpk(b, a)

其中：

b是传递函数的分子多项式的系数（一个一维数组），按降幂排列。

a是传递函数的分母多项式的系数（一个一维数组），按降幂排列。

函数返回三个值：

z是传递函数的零点的数组，按照复数的形式返回。

p是传递函数的极点的数组，按照复数的形式返回。

k是传递函数的增益值。

使用signal.tf2zpk函数可以方便地将传递函数的有理表示转换为零点-极点-增益形式，进而进行零极点分析、滤波器设计和频率响应评估等操作。

传递函数的增益值是指在零极点分析中，传递函数对频率响应的整体放大或衰减的因子。在信号处理和控制系统中，传递函数描述了输入信号经过系统后的输出信号与输入信号之间的关系。

传递函数一般由分子和分母多项式的系数表示，例如：

H(s) = (b0s^n + b1s^(n-1) + ... + bn) / (a0s^m + a1s^(m-1) + ... + am)

其中，b0, b1, ..., bn是分子多项式的系数，a0, a1, ..., am是分母多项式的系数，s表示复频率。

传递函数的增益值可以通过对传递函数在频域的幅度进行评估来确定。幅度表示输入信号通过系统后的输出信号的增益或衰减程度。增益值是一个标量，通常用分贝（dB）表示。

传递函数的增益值可以提供有关系统的放大或衰减特性的信息。正增益表示系统在特定频率处放大输入信号，负增益表示系统在特定频率处衰减输入信号。增益值的大小决定了系统对输入信号的放大或衰减程度。

在零极点分析中，增益值通常与传递函数的常数项相关。对于传递函数H(s) = K * (b0s^n + b1s^(n-1) + ... + bn) / (a0s^m + a1s^(m-1) + ... + am)，增益值K即为常数项。

传递函数的增益值在滤波器设计、系统控制和信号处理等领域中具有重要意义。它可以影响系统的幅频响应、稳定性和动态特性，因此在分析和设计系统时需要考虑增益值的影响。

四、结论

零极点分析是信号处理和系统理论中一项重要的技术，通过观察滤波器的零点和极点在复平面上的分布情况，我们可以揭示滤波器的频率响应、稳定性和传输特性等关键信息。它在滤波器设计、频率响应评估和稳定性分析等方面具有广泛的应用。掌握零极点分析的原理和方法，可以帮助我们更好地理解和优化滤波器的性能，推动信号处理和系统设计的发展。通过实例展示和实用工具的使用，我们可以更直观地理解零极点分析的应用。深入探索零极点分析，我们能够揭开滤波器特性的奥秘，为我们的工程和研究提供有力的支持。