介绍主流的VIO初始化方案

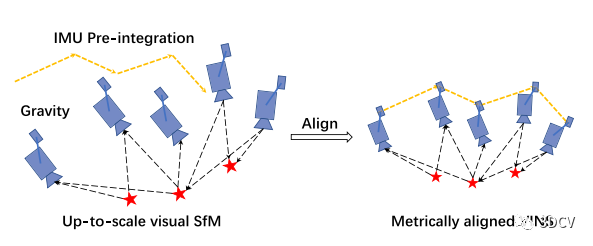
视觉惯性融合技术应用于机器人和自动驾驶方面。单目相机和低成本IMU成为最佳选择。因为VIO系统的高度非线性，初值对视觉惯性系统很重要,但很难获得精确的初始状态。VIO初始化的主要意义有：（1）对齐相机的世界坐标系和惯性系，因此需要估计重力方向（2）为后续的VIO算法提供较为准确的初始参数和状态（尺度、IMU bias、初始速度）,使得算法可以快速稳定地进入正常运行阶段。良好的初始化对VIO算法的整体精度和鲁棒性至关重要。本文旨在介绍主流的VIO初始化方案

1 前言

目前的初始化方法分为松耦合（Vins-Mono、ORBSLAM3）和紧耦合方案（OpenVINS），松耦合方案用的较多，并且表现更好。从求解方法上，有滤波、图优化、闭式解三种方法。但是,滤波会很早将状态边缘化,会失去最优性。图优化由于计算复杂性高。大多数现有的初始化方法需要系统静止或已知初始状态。不能适应动态运动、空中初始化。闭合式解法缺乏传感器噪声模型。本文主要介绍基于VINS-Mono的松耦合方案。

2 问题概述

已知：（1）IMU 和图像时间戳已同步；（2）IMU 和相机外参数已知求解：尺度、图像帧的速度、重力方向、IMU bias

3 方法

3.1 进行单目结构重建（SFM）,获得up-to-scale的相机姿态和特征点位置

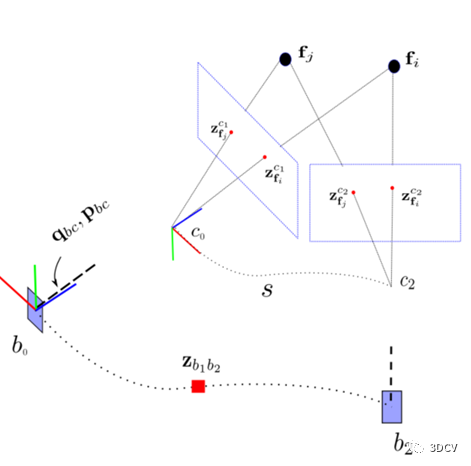
设定一定长度的滑动窗口，它维护了几个空间分离的图像帧。空间帧由足够的视差的图像帧来选择。选择两帧具有足够特征视差的帧。然后使用五点法恢复这两帧之间的相对旋转和带尺度的平移。然后任意设置尺度，对这两帧中观察到的所有特征进行三角剖分。基于这些三角化特征，采用PnP方法估计窗口中其他帧的姿态。

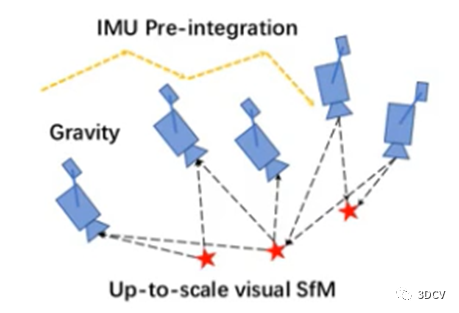
最后，应用全局BA最小化所有特征观测值的总重投影误差得到所有的帧姿态和特征位置。已知相机与IMU之间的外参数，则所有变量都可以从相机坐标系转换到IMU坐标系：

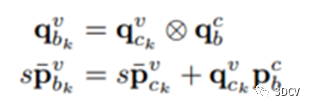
s是未知的尺度。

3.2 对IMU测量进行预积分,得到IMU的相对运动约束

预积分公式为：

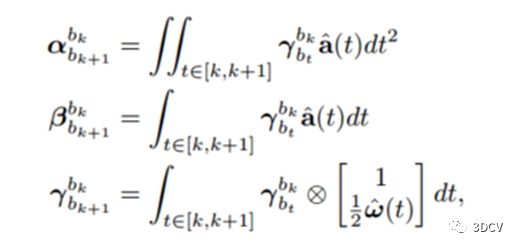
分别表示相对位置、速度和旋转约束。可以看出，惯性测量通常被积分以形成与图像帧的初始位置和速度无关的相对运动约束。

3.3 视觉惯性对准

我们已经得到了视觉SFM和IMU预积分中获得了相机姿势。本节将介绍对齐这两个轨迹的方法。

陀螺仪bias标定

窗口中两个连续的图像帧bk和bk+1，我们有来自视觉结构的相对旋转以及来自IMU预积分的相对旋转约束。通过最小化两者之间的误差来估计陀螺仪的bias：

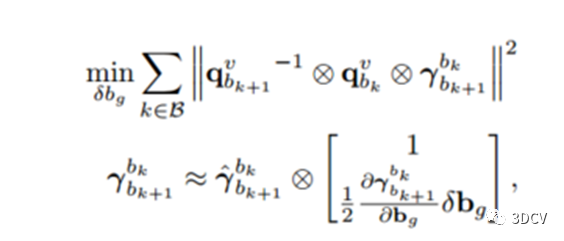
注意每次更新bg，都要重新计算预积分量。上面第二个式子用到了快速更新预积分量的方法。

估计速度、重力方向和尺度参数。

重力方向估计并强制其模长等于已知值。即需要估计的变量有

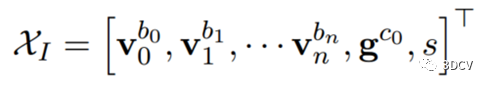
考虑预积分位置和速度相关的约束，IMU轨迹在相机坐标系c0下有：

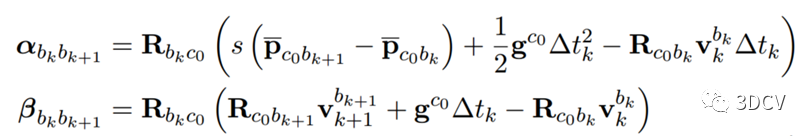
利用外参数，得到相机坐标系下的相机轨迹与预积分的关系：

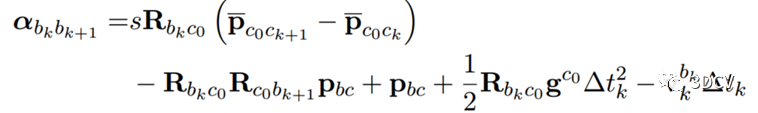
将待估计变量放到方程右边，有：

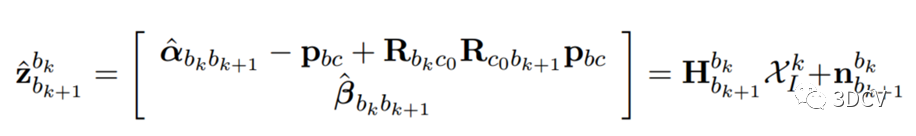
其中，

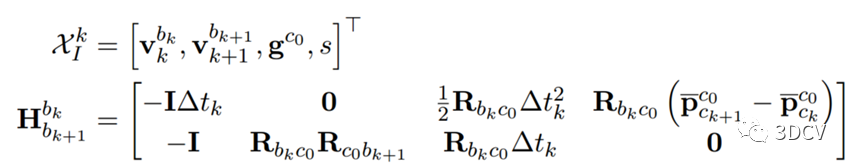
上式中，带尺度的相机位置和姿态已经通过视觉SFM获得。通过求解最小二乘问题：

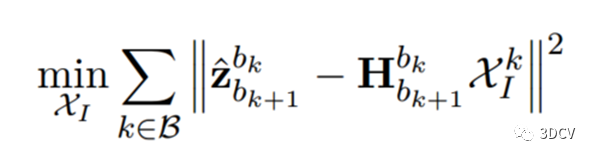
可以得到视觉坐标系下的速度和重力矢量，以及尺度。视觉结构的平移分量将被缩放到米制单位。通过强制范数约束，估计的重力将经历另一轮的细化。

重力方向细化

上面的优化中，并没有约束重力的大小。通过约束重力矢量的大小，可以对前一步得到的重力矢量进行细化。在大多数情况下，重力矢量的大小是已知的。但是，如果我们直接将这个范数约束加入到上面的优化问题中，就会变得非线性，难以求解。在这里，VINS-Mono使用一种方法通过优化其切线空间上的二维误差状态来强制执行重力范数。

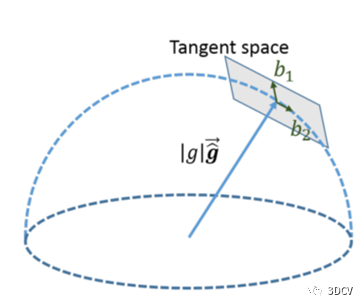
上图表示重力方向参数化示意图。由于重力的大小是已知的，重力的自由度为2，我们可以在它的切空间上用两个变量来参数化重力。我们将重力参数化为：

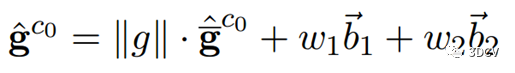
b1和b2是张成切平面的两个正交基。w1和w2分别是指向b1和b2的位移。我们可以用Gram-Schmidt过程(一种构造单位正交基的方法)很容易地求出b1、 b2的集合。这样，我们在其切空间上用两种状态重新参数化重力，然后将g替换为上式，也是线性形式。重新优化上面的最小二乘问题，迭代几次，直到g收敛。在细化重力矢量之后，我们根据重力矢量将所有变量从视觉坐标系旋转到世界坐标系（重力方向和Z轴平行的坐标系）：

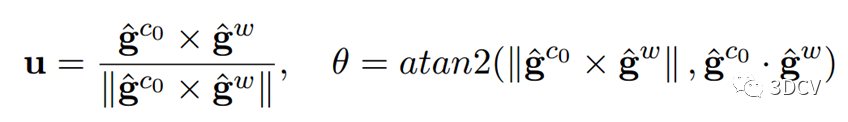
4 结论

此时，初始化过程完成，这些变量将被输入到一个紧密耦合的非线性视觉惯性估计器，即VIO过程。还有几点需要解释：对于旋翼飞行器来说，直线运动或零加速度运动等简并运动是不可避免的。这时候在SFM窗口内的IMU测量可能无法使整个系统可见，我们可以通过检查初始化过程中的预积分的值来拒绝小的加速度运动，初始化过程只有在IMU测量中包含足够的激励时才开始。在初始化过程中，加速度偏差很难标定，因为加速度通常在小旋转下与重力耦合。因此该方法不涉及加速度bias的标定。忽略加速度偏差不会对初始化结果造成显著的负面影响，可以在VIO过程中引入，这里不做介绍。

审核编辑：刘清