

技术干货 | 自制FOC驱动板
工业控制
描述
○ 1、电机原理 ○
1.1 左手定则
左手定则目的是为了判断通电导体在磁场中受力的方向,由英国电机学工程师弗莱明提出。
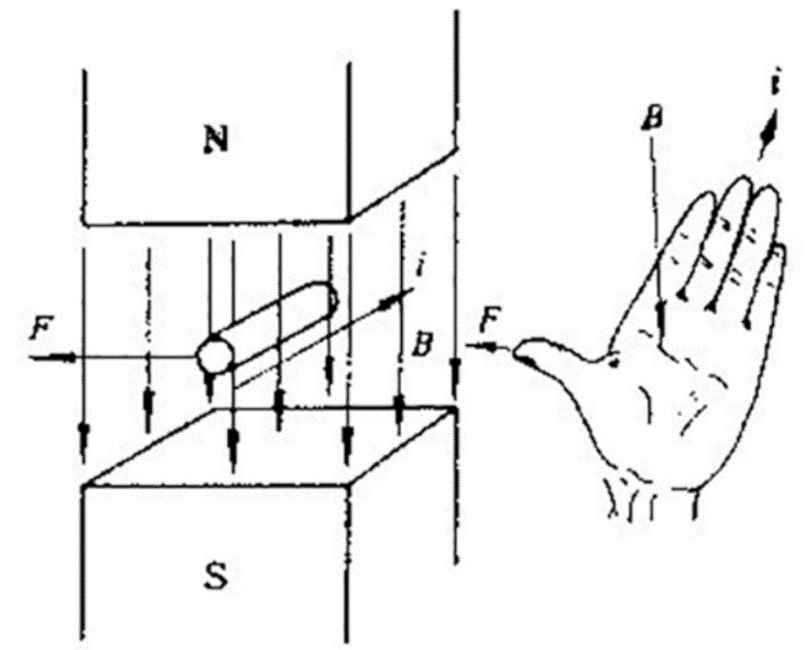
图1 左手定则
磁感线垂直穿过左手掌心,四指指向电流的方向,那么拇指指向就是导体受力的方向。导体所受的力为:

1.2 右手定则
右手定则目的是为了判断运动导体在磁场中产生的感生电动势方向。
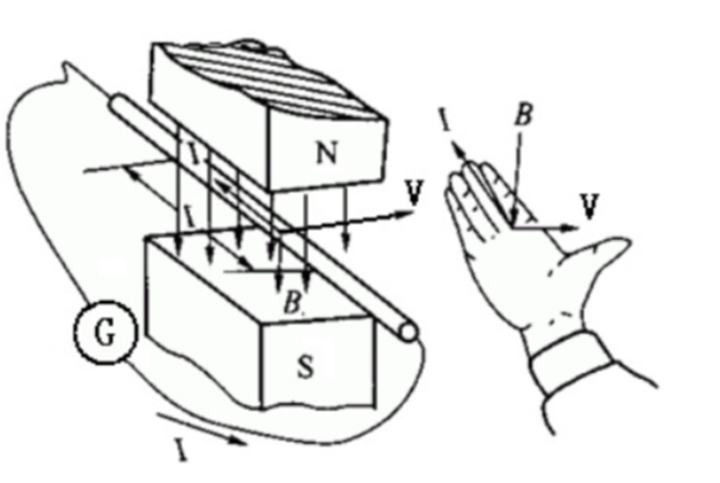
图2 右手定则
伸出右手,使大拇指跟其余四个手指垂直并且都跟手掌在一个平面内,把右手放入磁场中,让磁感线垂直穿入手心,大拇指指向导体运动方向,则其余四指指向感生电动势的方向。也就是切割磁感线的导体会产生反电动势,实际上通过反电动势定位转子位置也是普通无感电调工作的基础原理之一。
1.3 右手螺旋定则(安培定则)
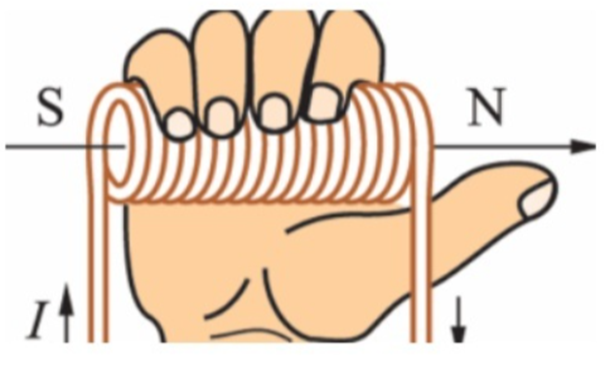
图3 右手螺旋定则
用于判断通电线圈磁场极性:用右手握螺线管,让四指弯向螺线管中电流方向,大拇指所指的那端就是螺线管的N极。对于直线电流磁场,大拇指指向电流方向,另外四指弯曲指的方向为磁感线的方向。
1.4 电机驱动原理
考察图4中的直流电机基本模型,电能—磁能—动能的转化,根据磁极异性相吸同性相斥的原理,中间永磁体在两侧电磁铁的作用下会被施加一个力矩,产生动能并发生旋转,这就是电机驱动的基本原理。
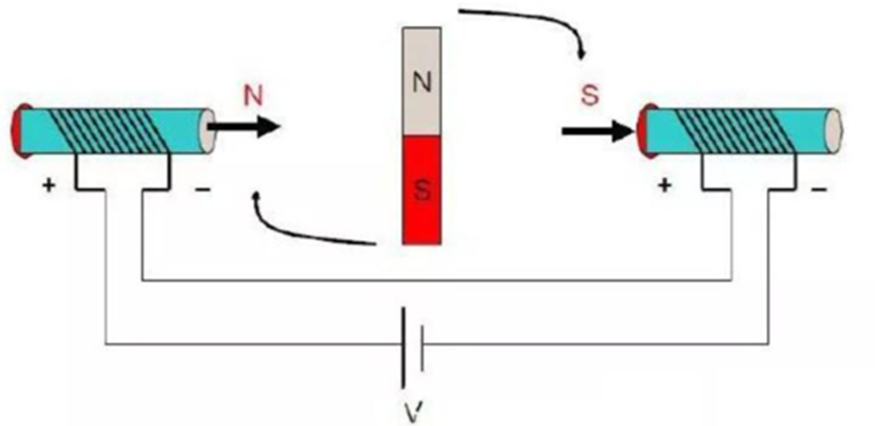
图4 电机驱动原理
可以看出,当中间转子磁场与定子磁场相互垂直时产生的力矩最大,相互平行时产生的力矩为零。要保证电机的持续转动,就要保证两磁场始终成一定角度以获取转矩。根据磁场换相方式,即可区分出有刷和无刷电机。
1.有刷电机驱动原理
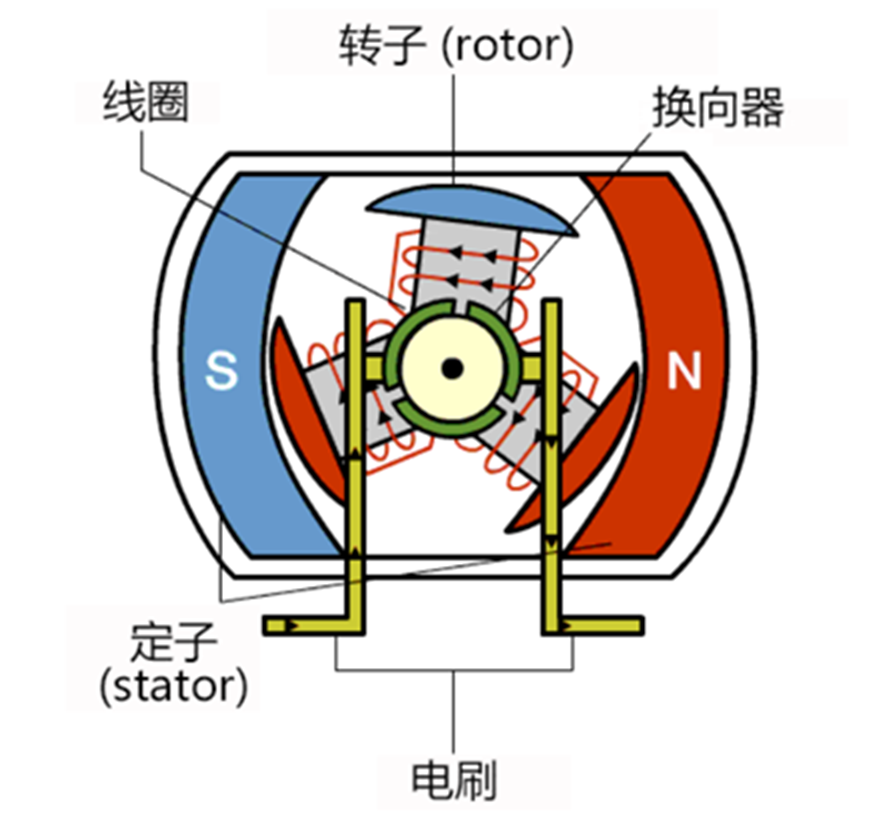
图5 有刷电机原理图
有刷电机,顾名思义为有电刷辅助磁场变化。直流有刷电机的主要结构就是定子+转子+电刷,定子磁场恒定不变,转子磁场借助电刷周期变化,通过磁场的相斥相吸作用获得转动力矩,从而输出动能。电刷与换向器不断接触摩擦,在转动中起到导电和换相作用。
2.无刷电机驱动原理
无刷电机,即没有电刷辅助换向,转子磁场不变,而是通过改变定子线圈的电压,从而产生变换的定子磁场,带动转子转动,产生动能。对于简化的无刷电机来说,以三相二极内转子电机为例,定子的三相绕组有星形联结方式和三角联结方式,而三相星形联结的二二导通方式最为常用,这里就用该模型来做个简单分析。无刷电机三相的连接方式是每一相引出导线的一头,而另一头和其他相两两相连。这个情况下假如我们对A、B极分别施加正电压和负电压,那么由右手螺旋定则可以判断出定子线圈磁极的方向。
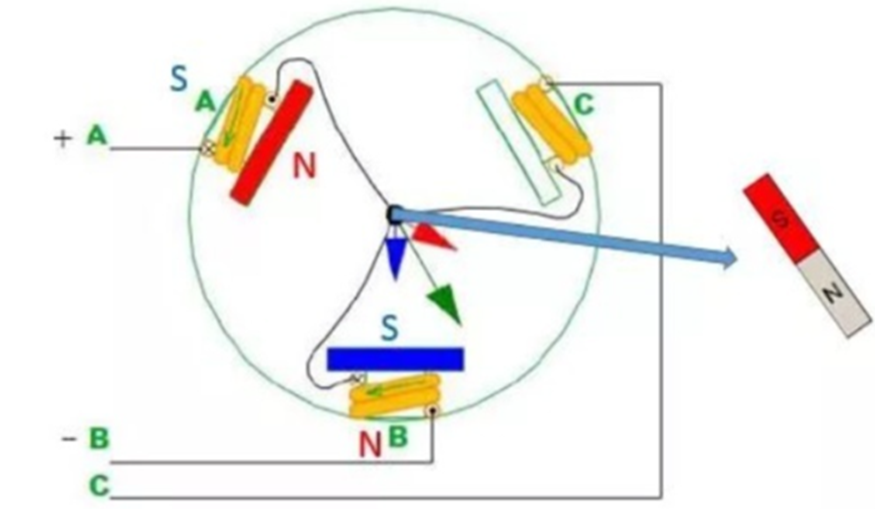
图6 无刷电机定子磁场方向
当定子线圈位于图6位置时,可知中间转子转到与定子磁场垂直的位置(CO)时产生的力矩最大,并将转子通过一推一拉的磁场力旋转至与定子磁场平行位置,达到稳定状态(力矩为零)。
同理,当转子力矩为零后,通过改变定子线圈的通电情况改变定子磁场方向,继续产生力矩使转子转动,从而实现电机的持续转动。
1.5 无刷电机的优势
相比有刷电机,无刷电机取消了电刷换向机构。这一特性使得无刷电机的运行损耗更小,寿命更长,适用于精密制造的无尘车间。借助FOC控制算法,无刷电机的位置、速度、力矩均可轻松调节,可实现定位、定速、力反馈等多模式控制。由于FOC算法能保持定子磁场与转子磁场始终相差90°,使电机能实现同等电流下最大力矩输出,运行效率高。
○ 2、FOC控制原理 ○
前面提到,当定子磁场与转子磁场相互垂直时,电机产生的扭矩最大;当定子磁场与转子磁场相互平行时,电机产生的扭矩最小。因此,要实现电机最高的运行效率与输出扭矩,应保证定子与转子磁场始终保持垂直。有刷电机通过增加转子换向器的节点数量提高运行效率,而无刷电机通过FOC算法拟合出垂直的定子磁场。下面将介绍无刷电机的FOC算法。
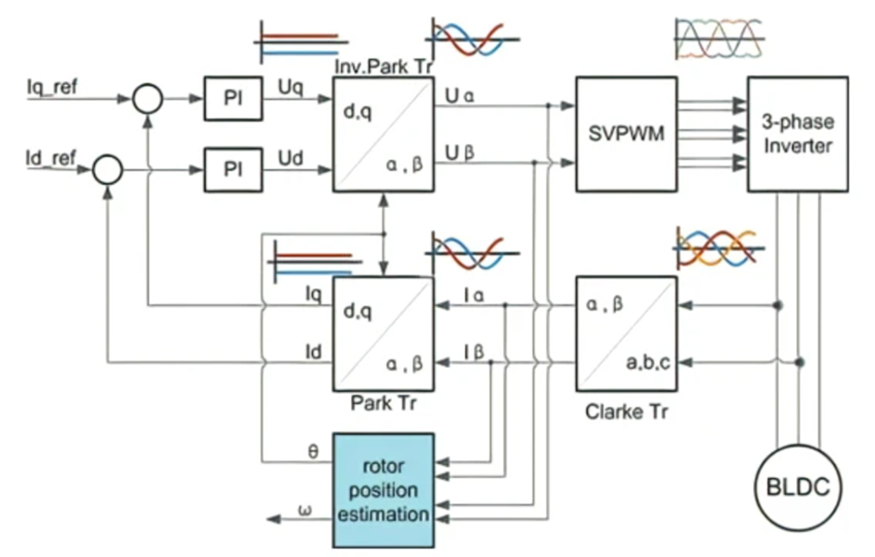
图7 FOC算法流程图
图7为FOC控制电流环流程图,目标是使电机的电流恒定,从而产生恒定力矩。
FOC控制算法的核心在于对三相交流电流的 解耦 ,将相互耦合的三相磁链通过Clarke变换和Park变换解耦为容易控制的交轴和直轴,通过PID控制器后,通过Inv-Park变换和SVPWM算法生成三相交流电驱动电机。下面,笔者将围绕FOC算法的各个流程进行讲解。
2.1 Clarke变换
在对电流进行采样后,能得到两两相位差为120°的三相正弦波电流,根据三角变换和基尔霍夫电流定律,我们可以将三相正弦波电流变化为两相正弦波。
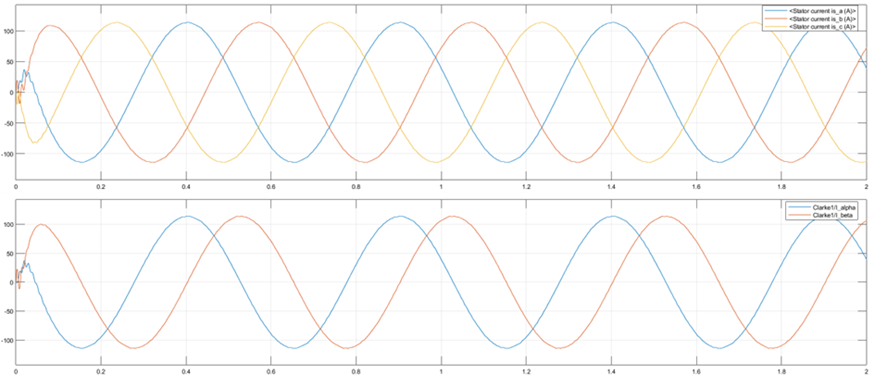
图8 Clarke变换(3s-2s)
三相对称正弦电流可以表示为:

根据表达式可画出三相电流的静止坐标系:
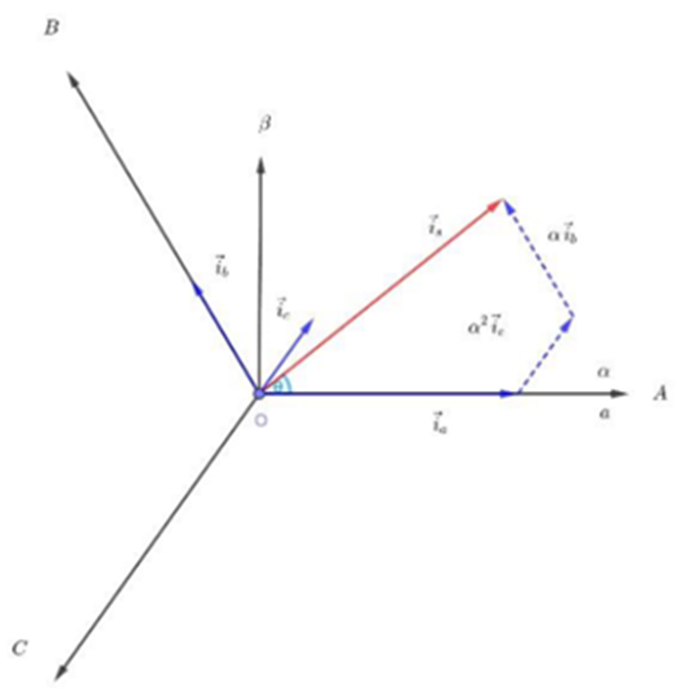
图9 Clarke变换坐标系
所谓Clarke变换,即将三相电流矢量在α轴和β轴上投影,可得到它们在两相坐标系上的分量:
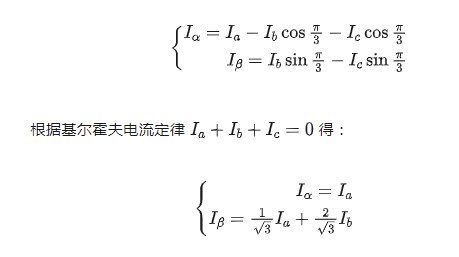
可以看到,通过Clarke变换,将三相正弦电流简化到二相静止坐标系,减少了一个变量。
2.2 Park变换
虽然通过Clarke变换,我们将三相正弦电流简化到二相静止坐标系,但是电流关系还未完全解耦,电流依然由时间和速度决定,因此还需要进一步变换,将α、β决定的两相静止坐标系变换为随磁场旋转的d、q坐标系。
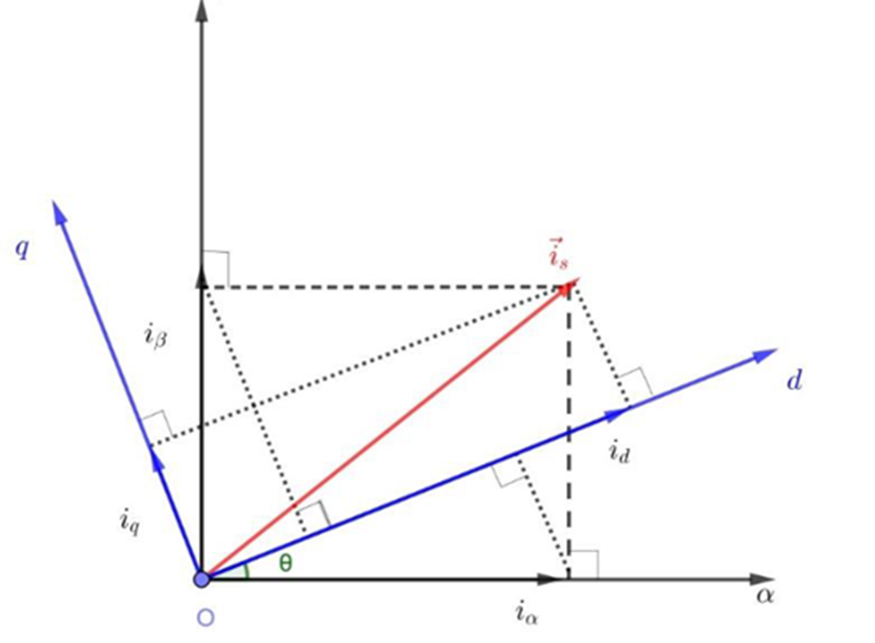
图10 Park变换
坐标系q轴垂直于定子磁场,称为交轴,d轴与定子磁场同向,称为直轴。角度θ为定子磁场与α轴的夹角。通过投影关系,可以推出park变换表达式:
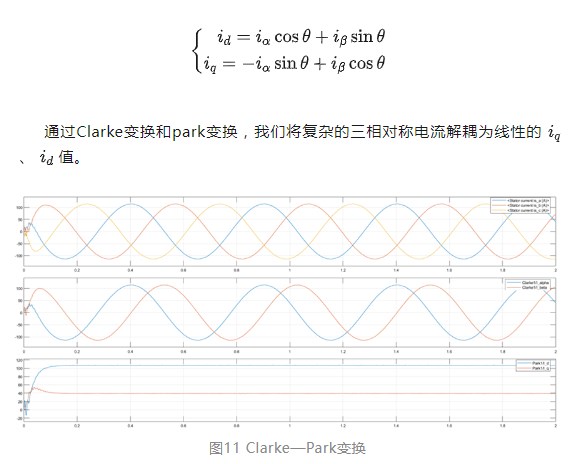
2.3 PID控制器
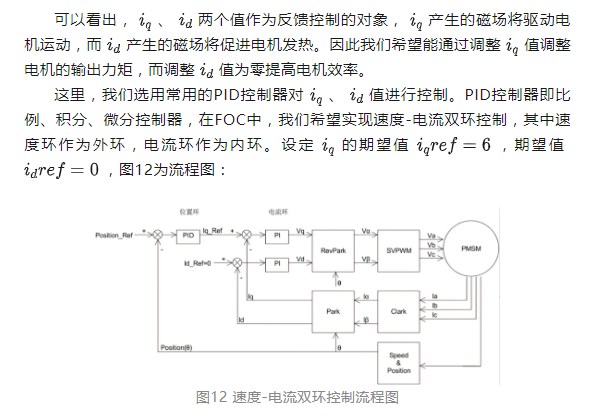
2.4 Inv-Park变换
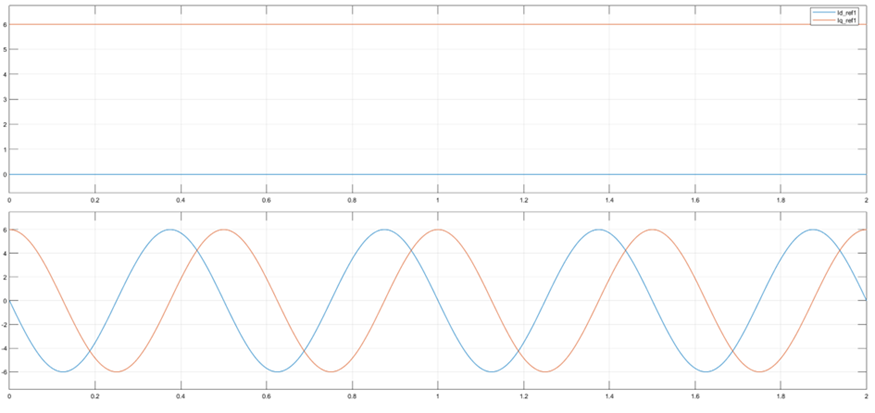
图13 Inv-Park变换

2.5 SVPWM技术
Inv-Park变换后,得到了两相静止坐标系下的 、 值,那么如何利用该值产生和之前一样的三相对称电流,从而 产生等效旋转磁场 ,这里就需要使用 空间矢量脉宽调制技术(space vector pulse width modulation) ,简称 SVPWM技术 。
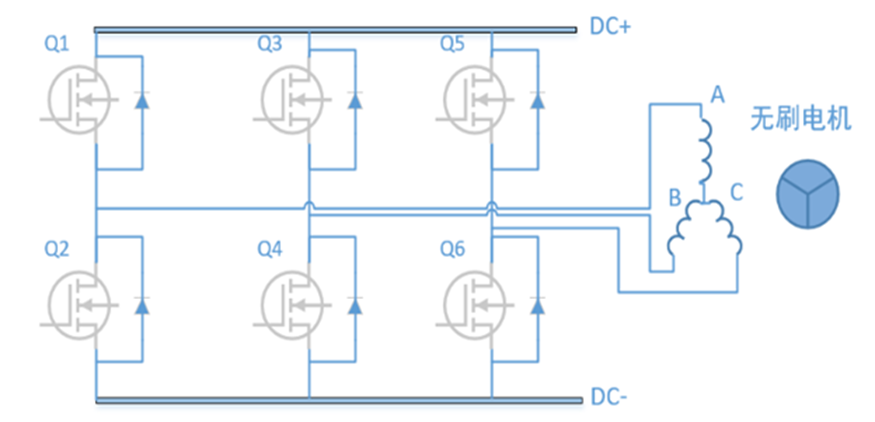
图14 三相逆变器驱动电路
无刷电机的驱动电路由六个NMOS功率管组成的开关电路构成,我们设定1为开,0为关。因此,总共有八种组合方式,对应八个电压空间矢量,其中,(000)和(111)为零矢量,剩余六个电压空间矢量((100)、(110)、(010)、(011)、(001)、(101))构成正六边形。
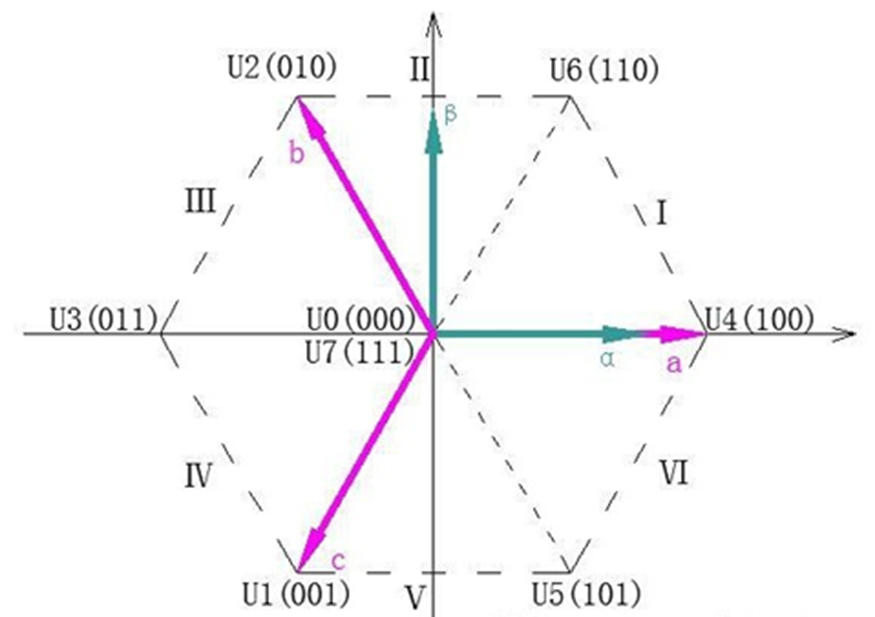
图15 abc坐标系和αβ坐标系矢量表示
根据 伏秒平衡原理 ,在一个开关周期内某个矢量的作用效果等同于两个相邻基础矢量分别作用不同时间的效果之和。因此,通过合理地配置不同基向量在一个周期中的占空比,就可以合成出等效的任意空间电压矢量了。
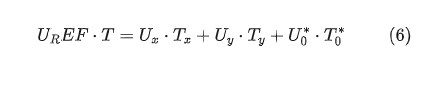
○ 3、Matlab仿真及软硬件实现 ○
通过Matlab的Simulink仿真,能帮助我们更好地理解FOC算法,同时验证其功能。下面将分别介绍FOC算法的开环和闭环控制仿真模型和效果。
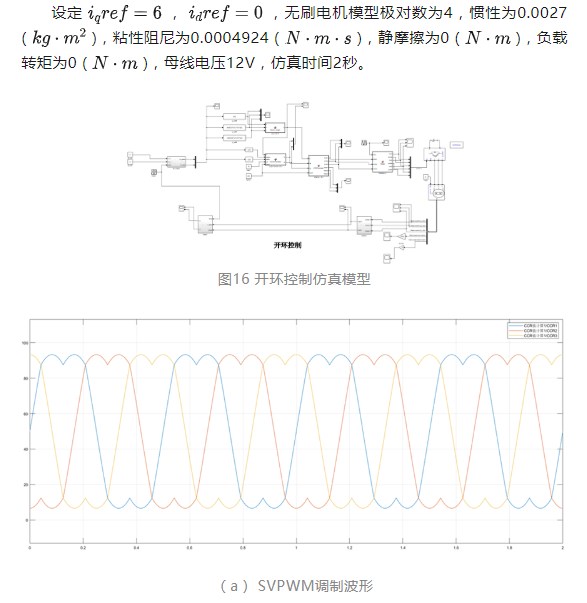
3.1 开环控制
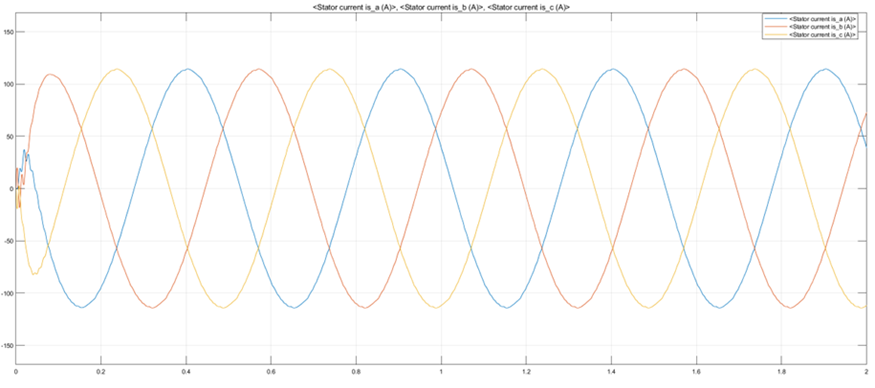
(b) 无刷电机三相正弦电流波形
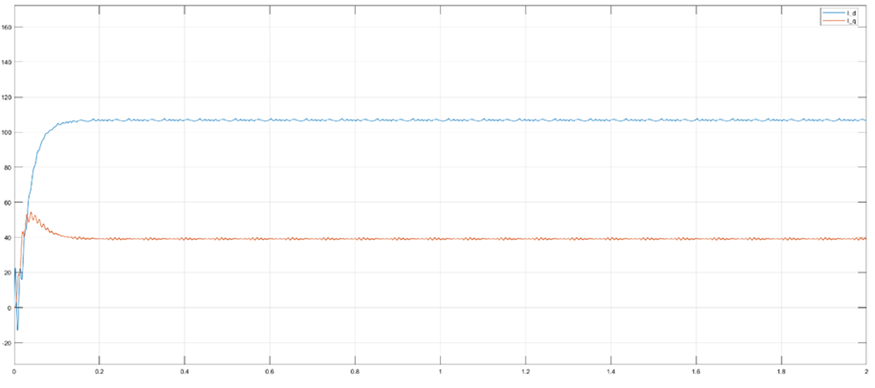
(c) Iq、Id值波形
(d) 电机开环运行速度波形
(e)电机开环运行力矩
图17 开环仿真结果

3.2 闭环控制
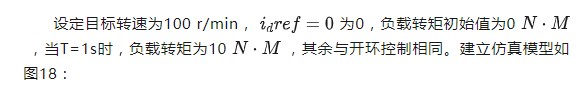
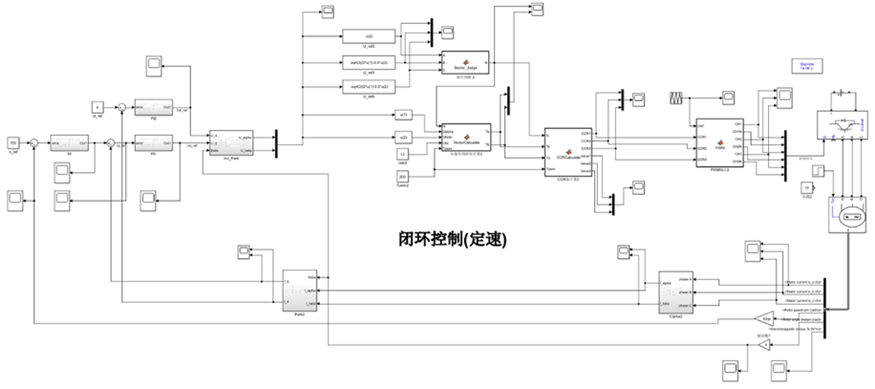
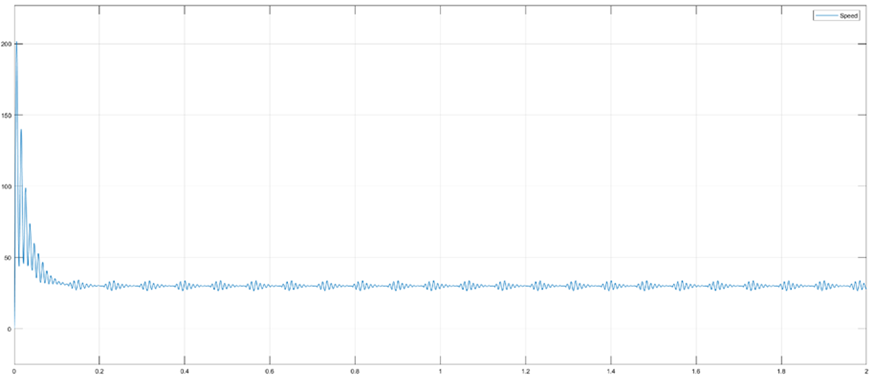
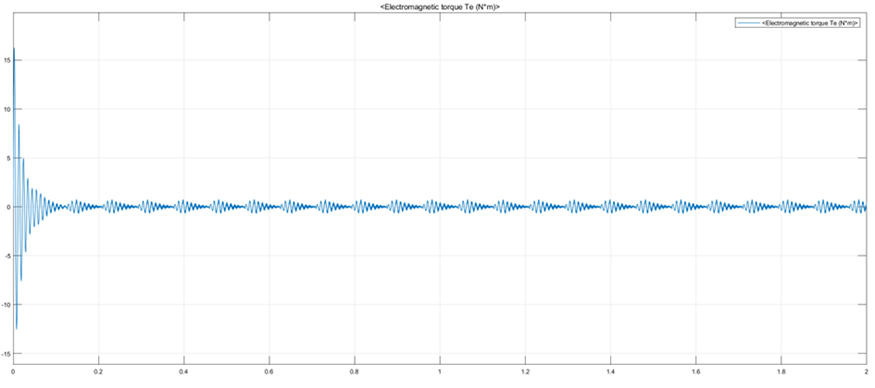
图18 闭环控制仿真模型
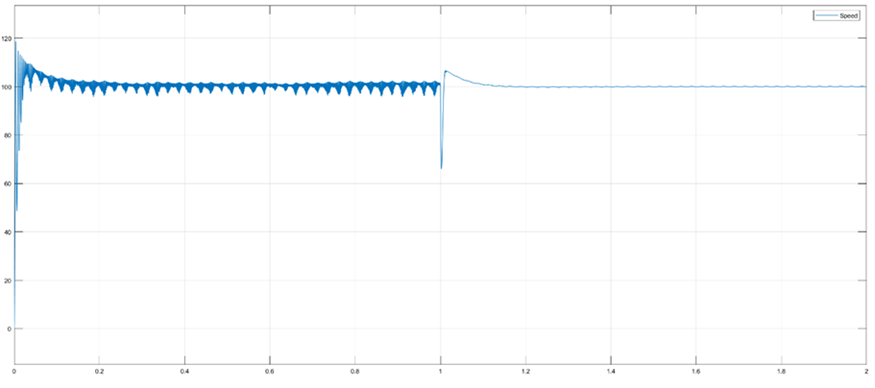
(a)电机闭环运行速度波形
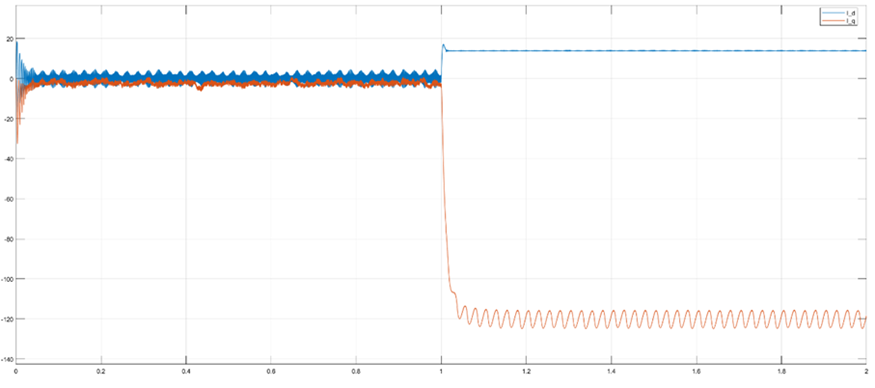
(b) Iq、Id值波形
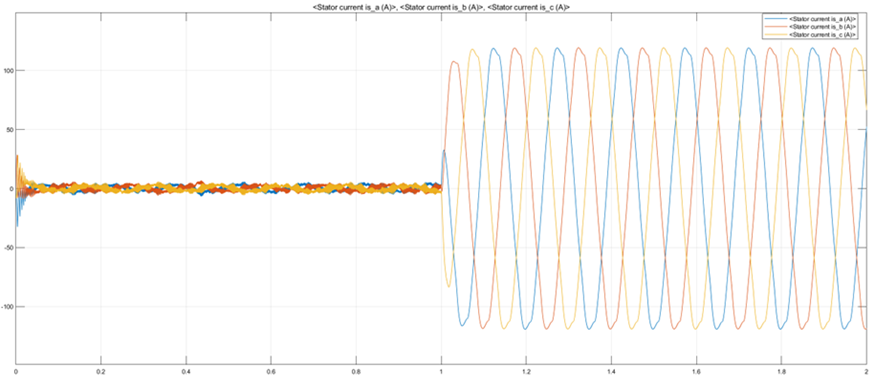
(c)无刷电机三相正弦电流波形
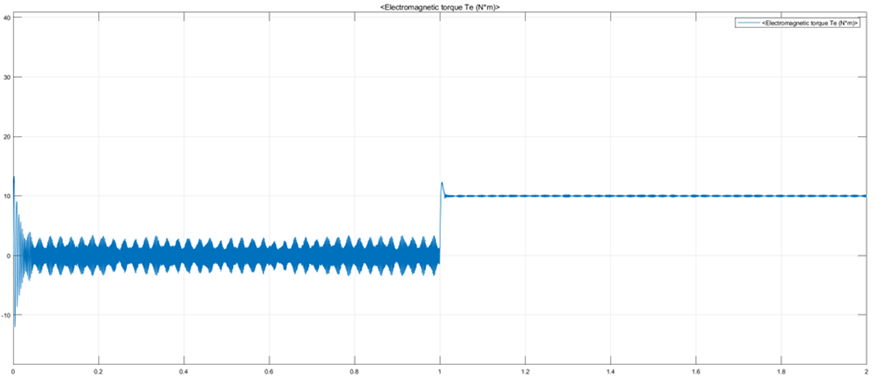
(d)电机闭环运行力矩
图19 闭环仿真结果
由图19仿真结果可以看出,电机实际转速能快速跟踪参考转速,d-q轴定子电流也有较快的动态响应速度,虽然d轴与目标值仍存在一定的静态误差,控制精度较低,但仍能验证该仿真模型的正确性。
○ 4、驱动板设计 ○
既然前面的理论基础和算法验证都已经完成了,那就让我们开始动手设计一块属于自己的FOC驱动板吧!
考虑到硬件成本、设计难度以及功率需求,本次设计参考开源项目simple_foc的硬件部分,主控选用STM32F103C8T6,驱动芯片选用DRV8313PWR,电流采样芯片选用INA240A2,外设支持USB(USART),SPI,CAN,SWD,整体采用12V电压供电,预估最大功率20W。
原理图
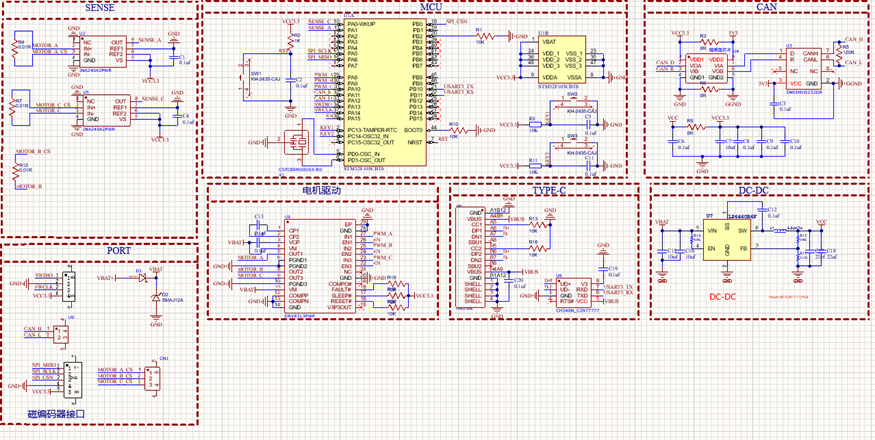
-
处处可见的FOC驱动电机技术2025-05-25 1378
-
电机驱动 C 位技术:有感 FOC 与无感 FOC 的本质区别2025-02-15 5580
-
FOC电机驱动技术解析 FOC电机使用注意事项2024-11-21 3435
-
请问foc驱动板上可以用esp32吗?2023-08-07 424
-
【技术干货】为什么电机FOC控制越来越流行?2022-07-14 2279
-
FOC控制驱动器的原理是什么2021-12-21 1777
-
深入浅出讲解FOC算法与SVPWM技术2021-08-30 2097
-
【文章分享】FOC技术跟普通马达驱动技术的对比2021-03-31 5346
-
自制BLDC/PMSM电机驱动板汇总开源分享:PCB+元件库+程序+教程2019-11-05 33844
-
基于FOC5.3库IHM07自制板BLDC/PMSM电机驱动:原理图/器件库/参考程序/培训资料/交易教程及说明等全部汇总开源分享2019-06-11 3803
-
基于ST FOC5.3自制IHM08 V3板:无感/有感霍尔/有感编码器/转矩模式等参考程序/电路图等详细资料全部开源分享2019-05-28 6494
-
STM32F1的无刷电机foc开发板电路图2017-12-21 2475
-
干货-FOC控制精细理论2016-01-21 54963
全部0条评论

快来发表一下你的评论吧 !

