电池SOC估算中的安时积分与卡尔曼滤波的数值计算方法

接下来的Matlab数值计算，将以电池建模的foster型等效电路为基础，在连续时间内对电池进行系统同定。

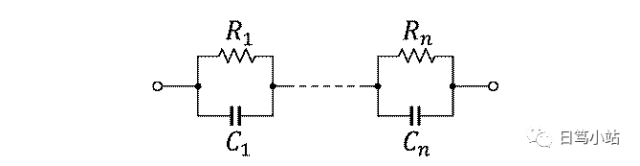
foster等效电路

首先，我们利用输入输出的数据来推测电池模型的参数。推测的参数为：

θ = [ R0 Rd Cd FCC SOC0 ] T

输入输出数据与SOC

电池的建模（Matlab)

数值实验用输入出数据的生成：

[ex_batt.m]1

%%假想实验数据的作成

Te = 2*3600; %实验结束时刻[sec]

Ts = 1; %采样周期[sec]

t = ( 0: Ts: Te );

N = length(t);

%输入（电流）的设定

u = 40sawtooth( tsqrt(2)) + 10*sin(t) - 18;

%输出（电压）的生成

SOC0 = 95; %初期SOC[%]

FCC = 40*3600; %满充电容量[C]

R0 = 0.450e-3; %电池内阻[ohm]

Rd = 0.500e-3; %扩散电阻[ohm]

Cd = 82000; %扩散电容[F]

th0 = [ R0, Rd, Cd, FCC ];

Nd = 3; %foster等效电路的近似级数

[ f, h, A, C, ymodel ] = batterymodel_foster(Nd);

%Simulation

[ y0, x ] = ymodel( u, t, th0, [SOC0; zeros(Nd, 1)] );

SOC = x(1, :);

%含有误差的采样值的模拟

um = u + randn(1, N) * 0.1; %电流传感器的误差

ym = y0 + randn(1, N) * 0.01; %电压传感器的误差

%波形

figure(3), hold on

subplot(3,1,1); plot(t/60, u)

ylabel('Current [A]'), xlim([0 Te/60]), ylim([-100 50)]

subplot(3,1,2); plot(t/60, y0)

ylabel('Voltage [V]'), xlim([0 Te/60]), ylim([3.2 4.2)]

subplot(3,1,3); plot(t/60, SOC)

ylabel('SOC [%]'), xlim([0 Te/60]), ylim([0 100)]

xlabel('Time [min])，

上述 “m file” 里面使用的函数 “batterymodel_foster" ， 用以下方式记述。

[batterymodel_foster.m]

function [ f, h, A, C, ymodel ] = batterymodel_foster(Nd)

n = 1:Nd;

％参数矢量与物理常数的关系定义

R0 = @(th) th(1);

Rd = @(th) th(2);

Cd = @(th) th(3);

FCC = @(th) th(4);



A = @th blkdiag(0, -pi^2/4 * diag((2*n-1).^2)/Rd(th)/Cd(th();

B = @th [100/FCC(th); 2*ones(Nd,1)/Cd(th)];



f = @(x, u, th) A(th)*x + B(th)*u;

h = @(x, u, th) SOC2OCV(x(1,:)) + [0, ones(1, Nd)]*x+R0(th)*u;



%利用数值微分来计算SOC的雅可比数列

C = @(x) [numdiff(@SOC2OCV, x(1)), ones(1, Nd)];

%yhat:预测输出的函数

function [y, x] = proto_ymode(u, t, th, x0)

    x = lsim(ss(A(th), B(th), eye(Nd+1), 0), u, t, x0, 'zoh')';

    y = h(x, u, th);

end

ymodel = @proto_ymodel;

end

上述的雅可比数列A，C为状态推算时使用。

我们再来看看偏微分的数值计算。

[numdif.m]

function [dfdx] = numdiff(f, x)

n = length(x);

h = eye(n)*1e-5;

dfdx = arrayfun(@(k) (f(x+h(:, k)) - f(x-h(:,k)))/(2*h(k, k)), 1:n);

end

另外，SOC-OCV特性的简易模型我们可以用以下m file来记述。

[SOC2OCV.m]

function ocv=SOC2OCV(SOC)

%系数设定

E0 = 4.14;    

K1 = 0.237;

K2 = -0.0516;

K3 = 1.05e-3;

K4 = 0.183;



mode = @(soc) E0 + K1.*log(soc/100) + K2.*log(1-soc/100) - K3./soc*100 - K4.*soc/100;

ocv = model(SOC);



ocv(SOC  >98) = numdiff(model, 98)*(SOC(SOC >98)-98) + model(98);

ocv(SOC<  2) = numdiff(model, 2)*(SOC(SOC< 2)-2) + model(2);

end

下面继续［ex_batt.m]来进行连续时间里的电池系统同定，转而来推算模型的参数。

[ex_batt.m]2

％％连续时间系统同定

yhat = @(th) ymodel(um, t, th(1:4), [th(5); zeros(Nd, 1)]);

%初期推算值

thhat0 = [1e-3, 1e-3, 1e5, 30*3600, 80];

%输出误差最小化的参数推算

thhat = Isqnonlin(...

@(th) ym-yhat(th.*thhat0), thhat0./thhat0, [ ], [ ],...

            optimoptions(@Isqnonlin, 'Display', 'iter',...

            'Algorithm', 'levenberg-marquardt')) .*thhat0

综如上述所诉，在连续时间内利用系统同定的方法，从实验得到的输入输出数据，可以定义内含物理现象的电池模型的参数。

电池状态的推定

众所周知，电池的状态主要包括SOC（剩余电量）和SOH（剩余寿命）。

SOC的推定方法可以总结为：

1. 依据放电试验的SOC测定
2. 基于电池端子电压的SOC推定
3. 基于OCV测试的SOC推定
4. 依据安时积分法的SOC推定
5. 基于模型的SOC推定

SOH的推定方法可以总结为：

1. 利用完全充放电测试容量的SOH推定
2. 依据内部电阻查表的SOH推定
3. Bookkeeping的SOH推定
4. 基于模型的SOH推定

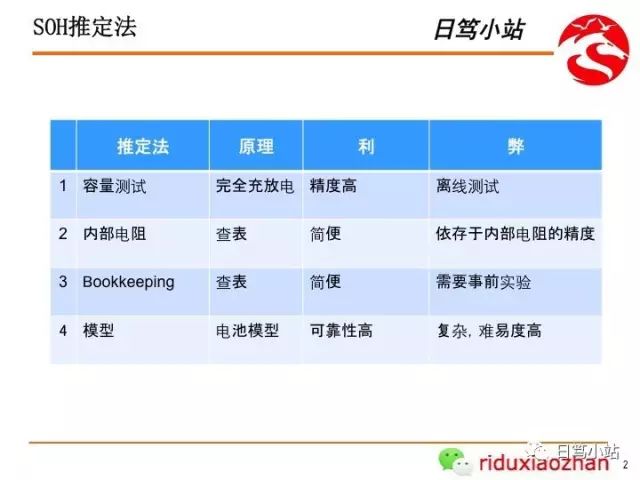
内部电阻的推定方法可以总结为：

1. 依据I-V特性（电流电压特性）的线性回归的内部电阻推定
2. 从step跳跃应答的内部电阻推定
3. 依据电阻测试的内部电阻推定
4. 基于模型的内部电阻推定

虽然有各种推算方法，但是我们需要根据：要求精度，使用环境，硬件条件，在线连续推定的必要性等等来具体判断用什么方法。

下面我们就给出比较复杂的利用卡尔曼滤波以及安时积分推算SOC的Matlab建模方法。

[ex_batt.m]3

%%利用EKF的状态推定

％离散时间的状态空间建模

f_ct = @(x, u) f(x, u, th0); %模型参数的固定

f_dt = c2d_euler(f_ct, Ts); ％euler法的离散化

%fd的雅可比数列

Ad = expm(A(th0)*Ts); ％f的雅可比解析计算

Q = diag([0.1Ts)^2, 1e-6ones(1, Nd)]); %系统外乱

R = 0.01^2; %观测外乱

xhat = zeros(Nd+1, N); %状态推算值

P = zeros(Nd+1, Nd+1, N); %推定分散

%初期推算值

SOChat0 = OCV2SOC(ym(1));

xhat(:,1) = [SOChat0; zeros(Nd,1)];

P(:,:,1) = diag([1e2, 1e-4*ones(1, Nd)]);

%更新时间

for k=2:N

[xhat(:,k),P(:,:,k)] =...

ekf(@(x) f_dt(x, um(k-1)), @x h(x, um(k), th0),...

@(x) Ad, C, Q, R, ym(k), xhat(:,k-1), P(:,:,k-1));

end

%表示结果

figure, plot_SOC(t, xhat(1,:), squeeze(P(1,1,:))',SOC);

EKF_RMSE = sqrt(mean((xhat(1,:) - SOC).^2,2));

%%安时积分法

SOC_cc = zeros(1, N);

SOC_cc(1) =SOChat(0);

for k=1:N-1

SOC_cc(k+1) = SOC_cc(k) + um(k)*Ts/FCC*100;

end

%表示结果

figure, plot_SOC(t, SOC_cc, [ ], SOC);

CC_RMSE = sqrt(mean((SOC_cc - SOC).^2,2));

上述euler的离散时间的状态方程式变化方法为：

[c2d_euler.m]

function fd = c2d_euler(fc, h)

fuction x_new = fproto(x, u)

    x_new = x + h*fc(x, u);

end

fd = @fproto;

end

SOC推算结果的表示

[plot_SOC.m]

function [ ] = plot_SOC(t, SOChat, P, SOC)

subplot(2,1,1), hold on

plot(t/60, SOC, 'r', 'LineWidth', 2)

plot(t/60, SOChat, 'b', 'LineWidth', 0.5)

xlim([0 t(end)/60]), ylim([0 100]);

xlabel('Time [min]'), ylabel('SOC [%]')

legend('True', 'Estimated', 'Location', 'Best')

box on



subplot(2,1,2), hold on

if ~isempty(P)

    hold on

    patch([t, fliplr(t)]/60,...

        [(SOChat-SOC-2*sqrt(P)), fliplr(SOChat-SOC+2*sqrt(P))],...

        ' ','FaceColor', [0.5, 0.5, 1], 'FaceAlpha', 0.5,...

        'EdgeAlpha', 0)

end

plot(t/60, SOChat-SOC, 'b')

plot([0 t(end)/60], [0 0], 'r', 'LineWidth', 2)

xlabel('Time [min]'), ylabel('Error [SOC%]')

xlim([0 t(end)/60]), ylim([-5 3]);

box on

end

上述为线性卡尔曼滤波的推算方法，非线性卡尔曼滤波的matlab建模方式基本相同，这里就不做介绍了。另外，本文是以EV为对象所建模，以HEV为对象时，由于电流波形的差异，推定的结果会有变故。HEV的刹车回生充电，内燃机回生充电，SOC都是在50%附近控制，所以对于输入的电流波形，不会有低频率的成分。

对于实际使用电池的系统来说，有着电池组内的误差，生产误差，环境温度误差等各项影响因素，所以未来我们使用模型推算电池状态时，不仅要考虑到这些误差因素的影响，更要考虑到锂电池材料进化的影响。未必复杂的算法适用于每个产品，我们需要根据实际的条件以及性价比等各种综合因素来挑选推算的方法，希望读者朋友们互相切磋，共同进步。