

看看全减器电路与Verilog
电子说
描述
半加器
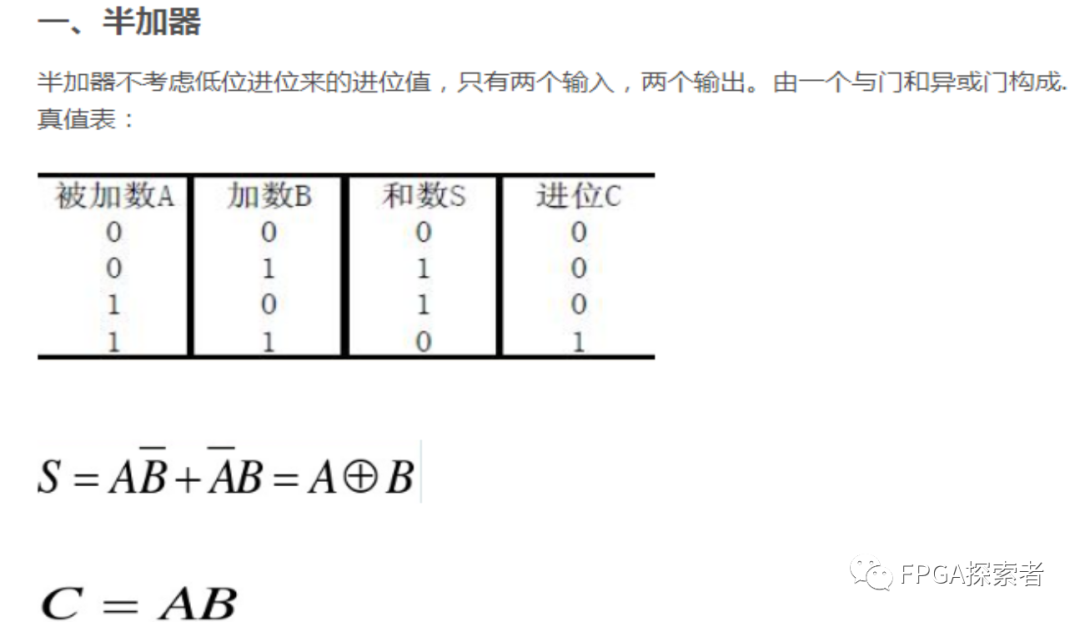
** 输入 A/B,输出和 S,输出 C 为进位。
**
** 输入 A = 0,B = 0,0+0 = 0,所以 S = 0,C = 0;
**
** 输入 A = 0,B = 1,0+1 = 1,所以 S = 1,C = 0;**
** 输入 A = 1,B = 0,1+0 = 1,所以 S = 1,C = 0;**
** 输入 A = 1,B = 1,1+1 = 10(二进制加法,进 1),**
** 所以 S = 0,C = 1;**
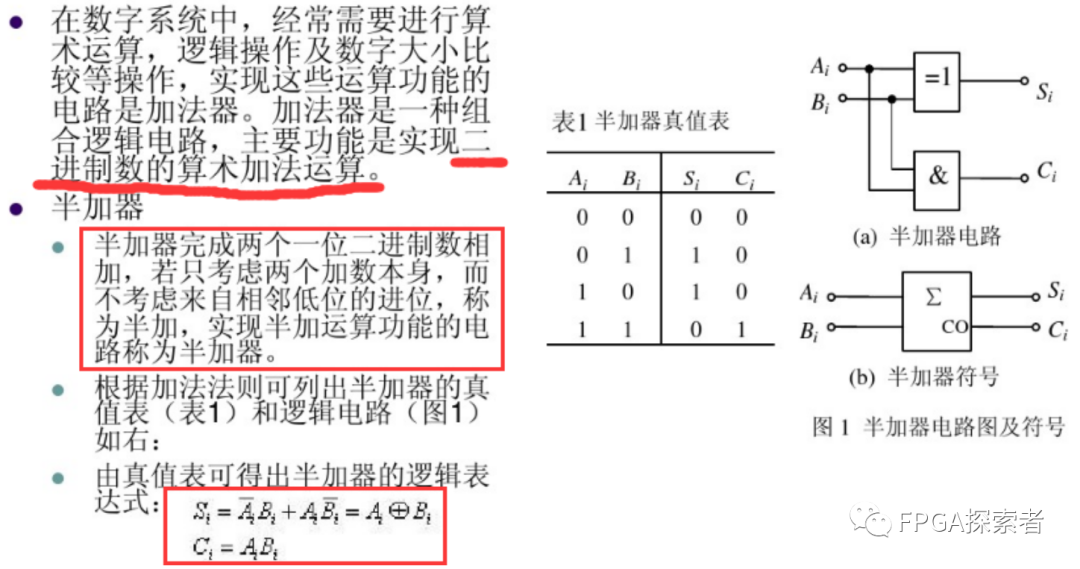
S = A ^ B // 输出加法结果
C = A & B // 输出进位结果
(1)根据真值表编写
按照半加器和全加器的真值表写出输出端的逻辑表达式,对半加器,输出的进位端是量输入的“与”,输出的计算结果是量输入的异或;对全加器,也按照逻辑表达式做。
//半加器模块
module adder_half(
input a,
input b,
output reg sum,
output reg cout
);
//这里的always @(*)搭配里面的“=”阻塞赋值符号
//实现的效果和 assign sum = a ^ b; assign cout = a & b;是一样的
always @(*)
begin
sum = a ^ b;
cout = a & b;
end
endmodule
全加器
当多位数相加时,半加器可用于最低位求和,并给出进位数。第二位的相加有两个待加数和,还有一个来自前面低位送来的进位数。这三个数相加,得出本位和数(全加和数)和进位数,这种就是“全加”。
真值表:
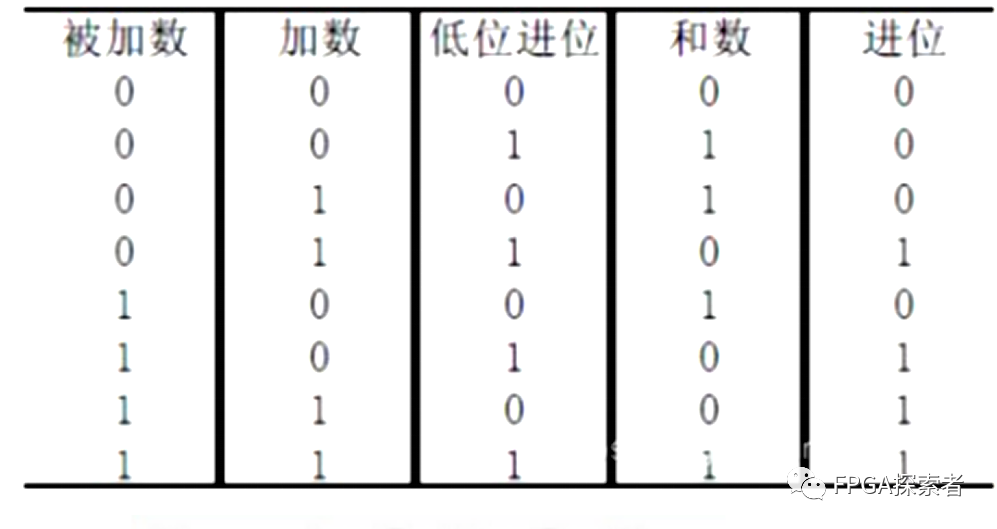
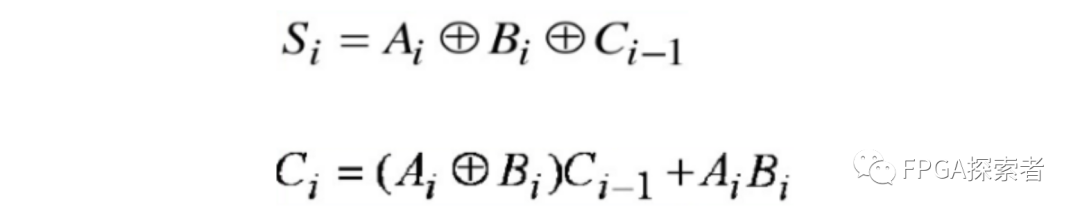
使用与门、或门和异或门搭建电路:
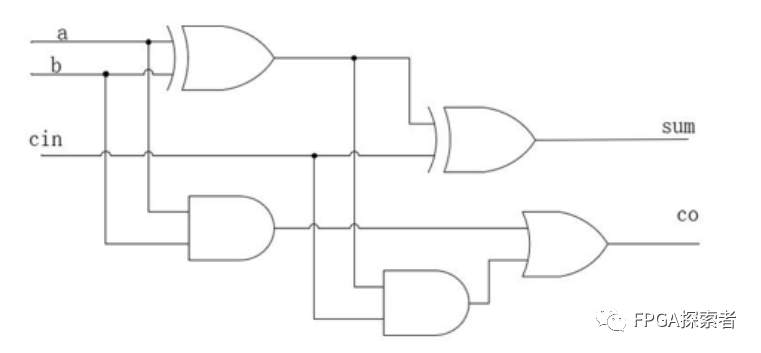
根据真值表编程,门级描述:
// 全加器
module all_adder(cout,sum,a,b,cin);
input a,b,cin;
output sum,cout;
assign sum = a^b^cin;
assign cout = (a&b)|(a&cin)|(b&cin);
endmodule
全加器编程其他思路
直接描述功能,加法直接得到低位的和、高位的进位。
这种方式描述简单,易于扩展,但是底层具体的实现方式比较抽象。
// 1 位全加器
module full_add1(a,b,cin,sum,cout);
input a,b,cin;
output sum,cout;
assign {cout,sum} = a+b+cin; // 位拼接,直接描述功能
endmodule
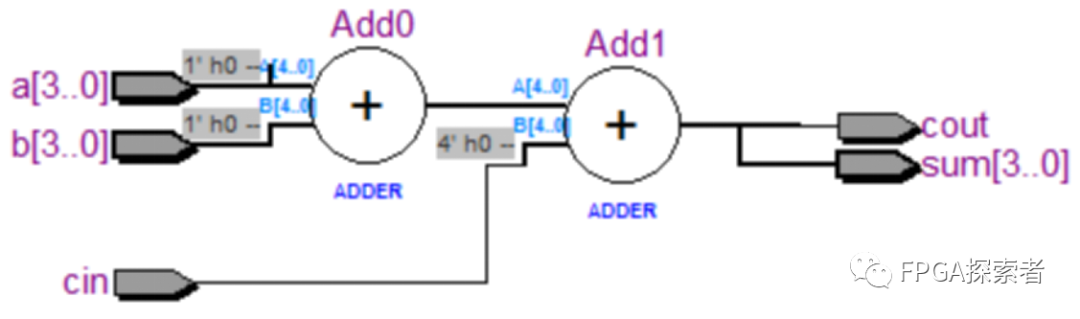
扩展,4 位全加器,运算不需要改变,只需要更改位宽:
module add4(cout,sum,a,b,cin);
input[3:0] a,b;
input cin;
output[3:0] sum;
output cout;
assign {cout,sum}=a+b+cin;
endmodule
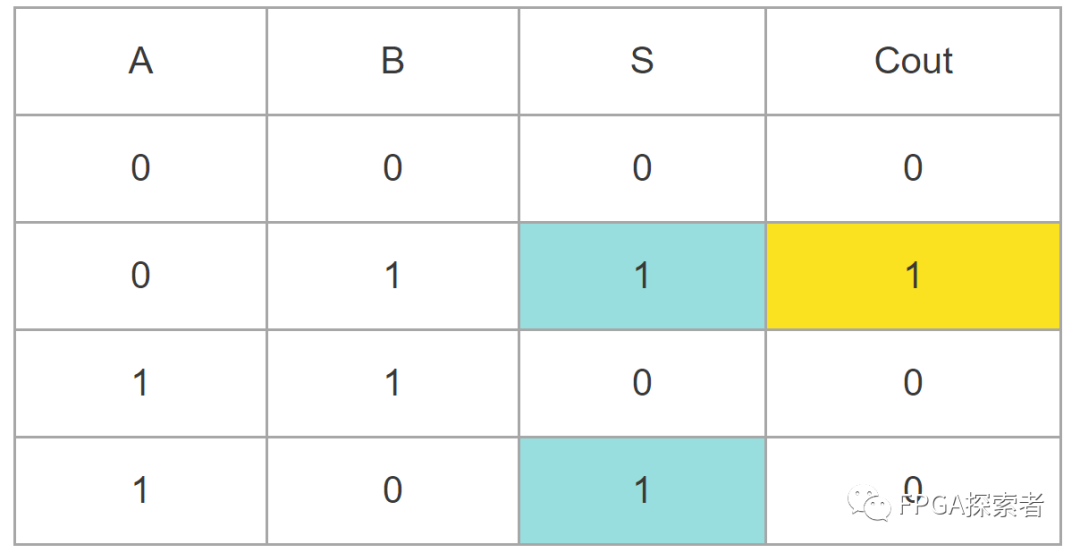
半减器
输入:被减数 A,减数 B
输出:差 S,借位 Cout
(1)0 - 0 = 0,不需要借位,所以 S = 0,Cout = 0;
(2)0 - 1 = 1,需要借位,所以 S = 1,Cout = 1;
(3)1 - 1 = 0,不需要借位,所以 S = 0,Cout = 0;
(4)1 - 0 = 0,不需要借位,所以 S = 1,Cout = 0;
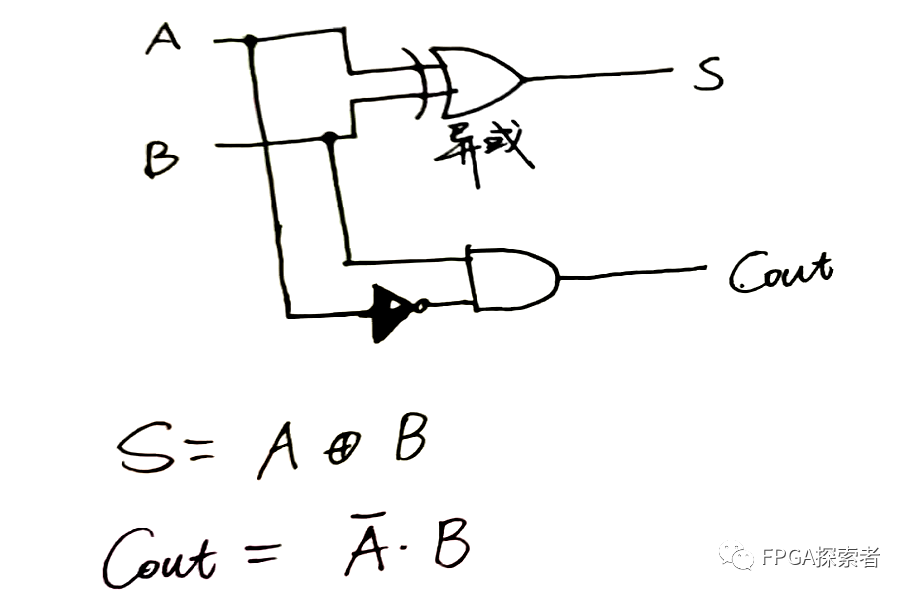
通过观察(或者卡诺图化简),可以得出
S = A ^ B;
Cout = (~A) & B;
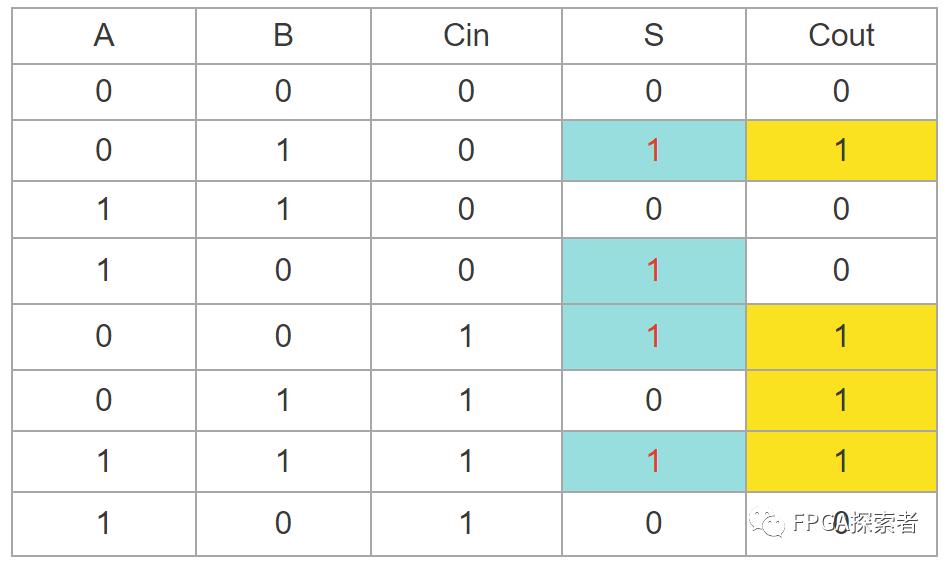
全减器
输入:被减数 A,减数 B,低位向高位的借位 Cin
输出:差 S,借位 Cout
这里需要注意:需要计算的是 A - B - Cin
(1) 0 - 0 - 0 = 0,不需要借位,所以 S = 0,Cout = 0;
(2) 0 - 1 - 0 = 1,需要借位,所以 S = 1,Cout = 1;
(3) 1 - 1 - 0 = 0,不需要借位,所以 S = 0,Cout = 0;
(4) 1 - 0 - 0 = 1,不需要借位,所以 S = 1,Cout = 0;
(5) 0 - 0 - 1 = 1,需要借位,所以 S = 1,Cout = 1;
(6) 0 - 1 - 1 = 0,需要借位,所以 S = 0,Cout = 1;
(7) 1 - 1 - 1 = 1,需要借位,所以 S = 1,Cout = 1;
(8) 1 - 0 - 1 = 0,不需要借位,所以 S = 0,Cout = 0;
对 Cout,不容易观察其表达式,使用卡诺图化简:
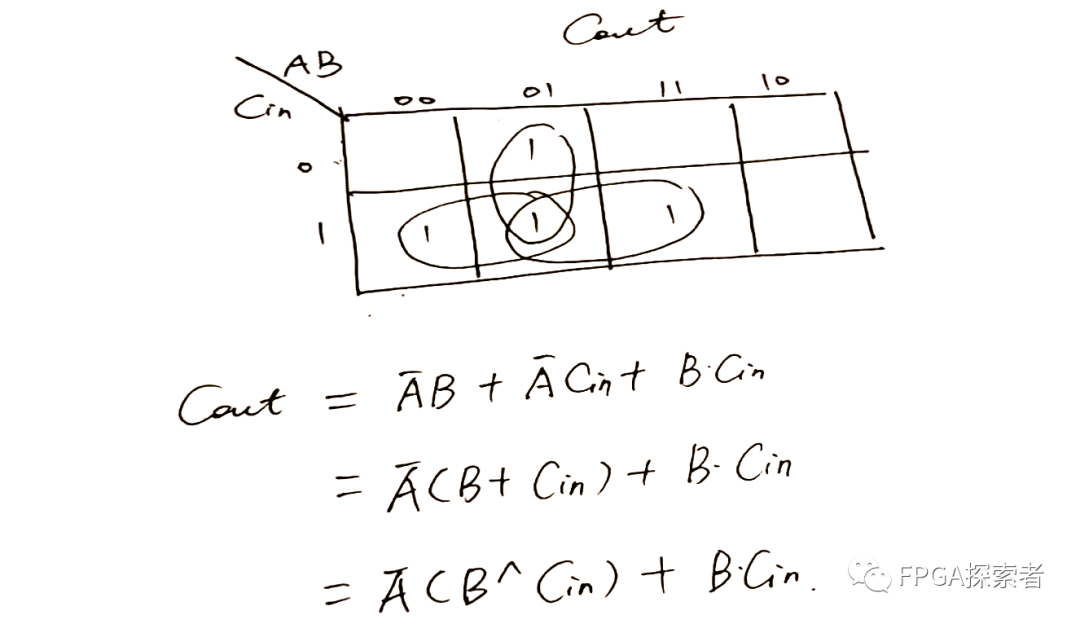
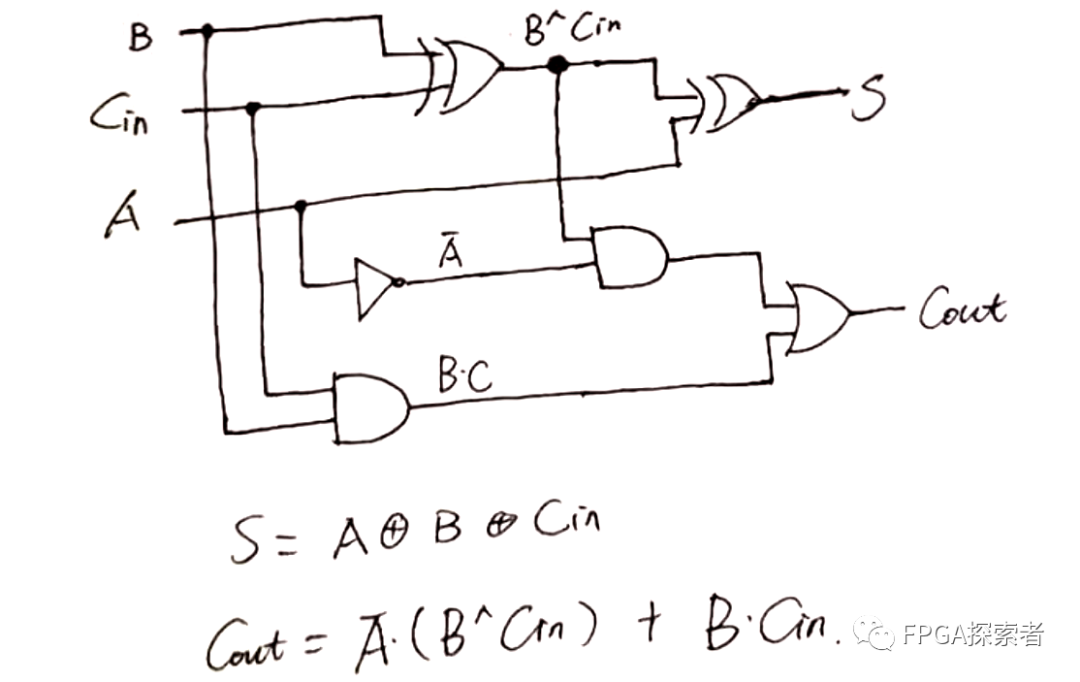
S = A ^ B ^ Cin
Cout = (~A) & ( B ^ Cin ) + B & Cin
-
看看两个使用Verilog HDL设计的简单电路2023-09-17 2640
-
如何使用Verilog HDL描述可综合电路?2021-04-04 4850
-
请问如何用74LS138和与门实现一位全减器2019-10-29 8544
-
Verilog语法基础2019-03-08 13722
-
用74ls138实现一位全减器2017-10-31 244443
-
8051core-Verilog2016-05-24 698
-
Verilog 黄金指南2016-05-20 577
-
Verilog+HDL实用教程-电科2016-05-11 708
-
学生作品:怎样做一个四位全减器啊2015-05-30 4023
-
北大verilog课件,大家都来看看啊2013-04-27 1764
-
Verilog典型电路设计2009-08-03 507
全部0条评论

快来发表一下你的评论吧 !

