功能安全的可靠性方程

混频器

这是数学极客的一个，他们甚至可以提供额外的见解和更正。即使你不是数学极客，我相信功能安全领域的每个人都需要了解这些方程式。在某些时候，您将不得不调用其中的一个或多个。我将尝试对方程有一个直观的感觉，所以希望它不会太糟糕。我确信在我下面的严格数学意义上存在错误，但希望它足够准确，可以理解含义并让您对这个主题有良好的感觉。

此处显示的方程显然是针对随机硬件故障的，而不是系统故障模式，因为如果出现正确的条件，系统故障模式的发生概率将为 1。

IEC 62308的范围规定“本标准描述了项目的可靠性评估方法。适用于任务、安全、业务关键、高完整性、复杂电子产品。它包含有关为什么需要可靠性以及如何以及在何处使用评估结果的信息。最后，它详细说明了如何选择可靠性评估方法以及支持评估所需的数据。

所以，让我们陷入方程（1），它实际上看起来最令人生畏。谁不喜欢积分和指数的混合？

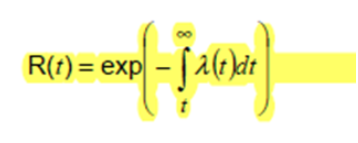
图2 - 项目随时间推移的可靠性的第一个方程

第一个等式给出了一个项目的可靠性，假设故障率与时间有关。在时间 0 R（t）=1 和时间 = 无穷大时，可靠性为 R（t）=0。R（t）可以说显示了可用性，在时间t仍然存活的设备比例，这就是为什么积分系数从t到无穷大代表所有尚未失效的设备，这让我想起了关于健康只是你可以死亡的最慢速度的笑话。R（t） 的对正数是 F（t），表示在时间 t 之前发生故障的设备的比例，然后由 F（t）=1-R（t） 给出，其中“F”代表故障。

λ（t） 表示设备的故障率，随着时间的推移，该故障率可能是恒定的，也可能不是恒定的。对于功能安全，我们通常假设λ（t）是一个常量值λ，所以让我们这样做，这使我们能够简化和探索方程。然后我们有 R（t）=exp（-λt），这使得更明显的是，如果 t=0 R（t）=exp （0） =1 和 t=∞我们有 R（t）=exp（-∞） =0，所以一切都很好。

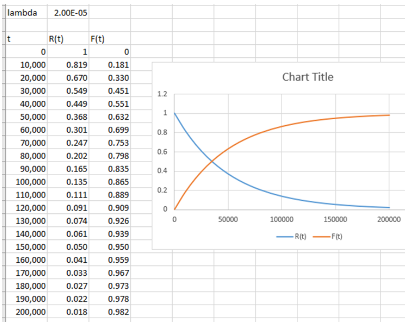
图 3 - 显示恒定故障率下大约 20 年内 R（t） 和 F（t） 形状的图

基于它在上述方程中的使用，λ（t） 表示设备在 t 到 t+dt 区间内发生故障的几率，前提是它已经存活到时间 t。它必须存活到时间t的事实意味着这被称为条件概率。条件是它必须幸存到那时才能在该间隔内失败。

对于功能安全，dt 通常为 1 小时，因此 λ（8760） 表示设备在其运行第二年的第一个小时内发生故障的概率，前提是它设法运行至少 1 年。

说明故障率是恒定的，这意味着如果一个设备已经存活了 1 年，它就有可能在 λ 的下一个小时内发生故障，如果一个设备已经存活了 20 年，它仍然有可能在 λ 的下一个小时内发生故障，λ 与它已经运行了多长时间无关。

注意 – 对于功能安全，我们通常对危险的未检测到故障率比实际故障率更感兴趣。设备无法进入安全状态主要是别人的问题。因此 λ 实际上更有可能是 λD危险故障率甚至λ的危险的未检测到的故障率。

顺便说一句，这意味着如果您在 10 年后用相同设计的完美新设备替换完全工作的设备，您将一无所获，因为在接下来的一小时内，两者都会有 λ 的故障率。

此外，值得提醒的是，如果设备的故障率为 1e-9/h，这并不意味着它会持续十亿年。相反，这意味着如果您有十亿台设备运行 1 小时，您可以预期其中 1 台在该小时内出现故障。同样，如果您只有 100k 个单位并且它们运行了一年，您可以预期其中一个在该年的某个时候出现故障。

让我们继续第二个等式。下面，f（t）显示为可靠性函数微分的负值，对于恒定故障率，这意味着R（t）具有平滑下降的形状（见上图3）。这意味着这种差分的负值将是正数（不确定负失败率意味着什么）。在严格的数学语言中，f（t）是失败概率密度函数。它还表示在 t 到 t+dt 区间内无条件地失效，即不需要存活到时间 t。与λ（t）相比，即使故障率恒定，1年后f（t）也会比20年后的f（t）高得多，因为大多数设备在此之前就已经失效了。当它达到20年时，它必须度过所有其他年份，因此在接下来的一个小时内它仍然失败的可能性非常小。如果 0.9 是预计存活 1 年的设备比例，如果预计在 1 年 + 1 小时存活的比例为 0.89，则 f（t）= （0.9-0.89）/1=0.01 在 1 年，即 delta R/delta t。从数学上看，如下所示。

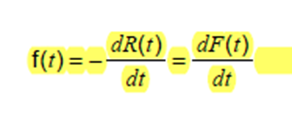
图 4 - 失效概率密度函数的第二个方程

注意 – 快速刷新。要区分 y=exp（f（x）） 使用 dy/dx = d（f（x）/dx））* exp（f（x））

让我们以常数故障率为例，使 R（t）=exp（-λt） 然后 d（R（t））/d（t）= -λexp（-λt） =-λR（t） 这样 f（t）=λR（t）。由于R（t）=1在时间0（所有设备仍然存活）和R（t）=0在时间无穷大，那么f（t）从λ到0，其中λ（t）是一个常数λ。

下面的第三个等式是用λ（t）替换λ并重新排列项。

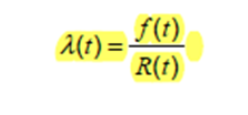
图 5 - 瞬时故障率的第三个公式

下图显示了条件失效率 λ（t） 和非条件失效率 f（t），绘制在大约 20 年的时间内，常数 λ（t） 为 2e-6/h。理论上，λ（t） 一直恒定到无穷大，但 f（t） “迅速”下降到零，因为没有设备会失效（在概率意义上）。

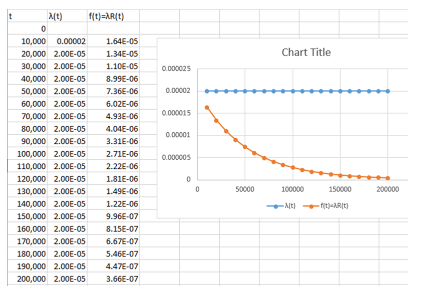
图 6 有条件和无条件故障率图

最后，我们只剩下可靠性和平均故障时间之间的关系。查看史密斯的书以获得指导，请考虑R（t）如下。如果有 N 个项目，并且 NS（t） 是在时间 t 时仍存活的设备数，则 R（t）=NS（t）/N。

注意 – NS 代表 N琥珀色 S孵化。

假设我们想知道在所有设备发生故障之前，N 个单元可以预期运行多少小时。在每个时间间隔内，总运行小时数增加 NS（t）*dt。因此，总运行小时数由 NS（t） wrt dt 的 0 到 ∞ 的积分给出。一个器件的平均预期时间为积分除以 N，但 NS（t）/N = R（t） 给出以下等式。

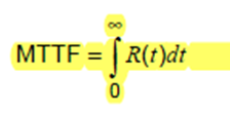
图 7 - 显示平均故障时间的第四个方程

推导清楚地表明了MTTF实际上是什么。如果您有 5 台设备，并且它们存活 100 小时、1000 小时、2000 小时、5000 小时和 10000 小时，则 5 台设备的总运行时间为 18，100 小时，MTTF = 18100/5 = 3620 小时。

最后，让我们总结一下IEC 62308中的方程式，以假设功能安全中通常发现的恒定故障率。

图 8 - 如果 lambda 是常数，则为上述等式

上面没有说明，但可以从数学中得出，如果 MTTF 为 X 并且故障率恒定，那么 63.2% 的项目将在 X 小时运行后出现故障。另外值得说明的是，对于假设的恒定故障率，1 台设备运行 1 万小时与 1 万台设备运行 1 小时相同。

您还可以以其他方式操作方程式。例如，如果一个IC的恒定故障率为1000 FIT它能存活20年的机会有多大。R（t）=exp（-1e-6*20*8760）=0.84。

希望这个博客能给你信心，不要害怕围绕可靠性的数学。希望它能让你能够尝试方程式。

审核编辑：郭婷