离散小波变换的FPGA实现(一)

傅里叶变换的局限性

在正式进入小波变换之前，我们不妨来讨论一下傅里叶变换的局限性和为什么我们需要引入小波变换。回想傅里叶变换的公式

• 从积分的算式我们可以轻松知道,在积分式一结束的同时, 另外一个谱的信息就会完全消失,就是说,傅里叶变换的频域上不含有时间信息
• 同时从积分的上下限我们也可以看到,当信号发生一些不平稳的变化的时候,傅里叶变换并不能很好的察觉到他的 幅度和位置 ,因为从表达式可以看到,傅里叶变化对每一个时刻的值都是平等对待的,而且所有的突变值也会被积分区间所平分.所以我们可以看到傅里叶变换对窄带信号检测不敏感,不能处理非平稳信号
• 从滤波的角度看,回想一下,当信号频谱和噪声频谱是相互分离的时候,我们总可以分离信号和噪声,通过一些加窗滤波的方法就可以了.但是如果 信号和噪声的频谱是混在一起的 ,那么,这个时候傅里叶变换就无能为力了,也就是说,滤波靠的是信号域和噪声域在频谱上的分离

短时傅里叶变换(STFT)

怎么来解决以上的问题呢?有人提出了短时傅里叶变换来加以改善,我们先来看看短时傅里叶变换的表达式:

在对信号的时频分析中,我们希望时间分辨率和频谱分辨率都可以比较高,但是从定义式里面我们就知道,时 间分辨率和频谱分辨率是相互制约的 ,同时也说明,我们没办法同时获得较高的时间分辨率和频谱分辨率.

从这里我们可以再一步印证出,傅里叶变换(连续)具有无穷的频谱分辨率,而无时间分辨率.

现在我们回来讨论短时傅里叶变换的窗函数 的长度N,显然N如果变大,频谱分辨率肯定是越来越好的,时间分辨率确实便来越差的.同时N如果变小,频谱分辨率肯定是越来越差的,时间分辨率便是越来越差的.

我们到底想要什么东西

既然上面说了时间分辨率和频谱分辨率已经是不可兼得的了,那么现在问题来了, 我们到底想得到什么东西? 回想一下: 傅里叶变换的缺点在他不能有效地处理非平稳信号,短时傅里叶变换的N是固定的,往两边变化都会有制约.

那我们能不能在分析的过程中让这个N变起来?让他 在信号变化快的时候窗变小一点 ,获得较高的时间分辨率,较低的频谱分辨率. 在信号变化慢的时候窗变大一点 ,获得较低的时间分辨率,较高的频谱分辨率.

这个时候就应该给大家引入小波变换了.大家可以先无道理地认为小波变换就是一个窗长度会变的傅里叶变换(虽然我一直不喜欢这个通俗的比喻...)

信号的正交表示

在正式讲小波变换前,需要先补充一些知识.

在信号分析中,我们常将信号展开成一组信号的线性组合,即有

当然这个是反着来用的,根据每个维度的特征值来合成回x(t),也就是逆变换

这里要注意的还有一点是,所谓的基函数,其实不仅仅是一个函数,而是一些有相同特征且相互正交的函数族.

小波展开与小波变换

小波函数

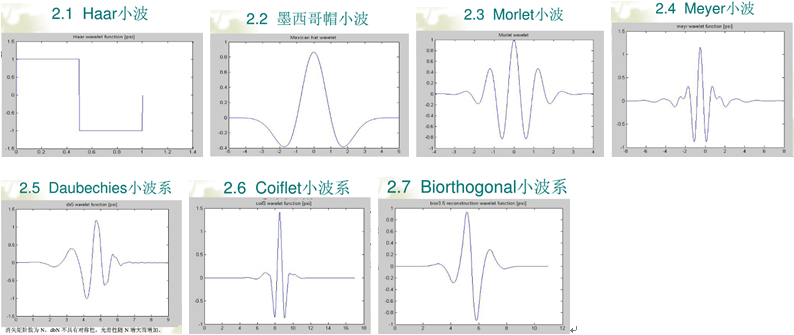
小波(wavelet)信号是一类衰减较快的波动信号,其能量有限,且相对集中在局部区域. 先来看看常用的小波函数: