

乱码电路第3部分:遗忘转移
描述
在我们的乱码电路系列的第 2 部分中,我们看到,如果我们有办法让 Alice 在 Alice 不知道 Bob 收到什么信息的情况下向 Bob 发送一些他需要的信息,那么可以私下评估任意函数(即,不透露要计算的函数的输入)。虽然这在直觉上似乎是不可能的,但发送方(爱丽丝)有一种方法可以向接收方(鲍勃)提供一组可能的消息,这样鲍勃从爱丽丝那里得到他想要的消息,但爱丽丝不知道鲍勃收到了哪条消息 - 即使她提供了消息!
要了解遗忘传输的工作原理,需要对公钥加密有一个基本的了解。公钥加密的每个用户都有两个数学上相关的密钥,而不是在用户之间共享私钥(与 AES 一样):私钥 k 只有用户知道,以及公钥 kG,其中 G 是公共参数。用户可以向任何人透露他们的公钥 kG,但绝不能透露他们的私钥 k。即使其他用户都知道 G 和 kG,也无法提取用户的私钥 k。
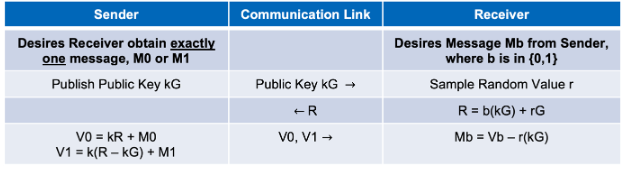
让我们来看看这个协议是如何工作的,以了解为什么接收方只能恢复一条消息,以及为什么发送方不知道收到了哪条消息:
发送方首先发布公钥值 kG,只有他们知道该值 k。即使 kG 和 G 都是公开的,其他人也不可能恢复 k。
接收方现在构造一个值,该值取决于他们想要的消息 M0 或 M1。此值必须被值 rG “屏蔽”,否则发件人将清楚他们选择的是哪条消息。
为了接收 M0,它们构造并发送 R = 0(kG) + rG = rG
为了接收 M1,它们构造并发送 R = 1(kG) + rG
由于发送方不知道值 rG,因此他们无法区分 (rG) 和 (rG + kG)。发送方现在构造并返回两个值 V0 和 V1。让我们根据接收方要恢复的消息来研究 V0 和 V1 是什么:

请记住,接收方只能访问 G、kG 和 r,因此他只能通过将随机值 r(他们选择)乘以发送方公钥 kG 来计算非盲值 r(kG)。接收方无法计算红色的盲值,因为接收方不知道 k。 请注意接收方如何通过从相应的 Vb 值中减去 r(kG) 来成功解盲他们选择的消息 Mb。但是,他们无法删除 V(1-b) 上的盲法,因为接收方不知道发送方的私钥 k 来计算 k(rG - kG) 或 k(kG + rG)。因此,接收方准确地恢复了他们请求的消息,而发送方不知道他们能够恢复哪条消息!
赋值器步骤 (鲍勃)
现在我们已经了解了 Oblivious Transfer 的工作原理,我们准备完成上一篇文章并完成评估任何函数的通用解决方案,而无需任何一方透露他们的输入。
Alice 生成乱码表后,将连线 1 和乱码输出列的输入键发送给 Bob。为了检索与鲍勃的输入位b对应的线路2的输入键,他与Alice进行了遗忘传输协议。这允许 Bob 只学习与他的输入位 b 对应的键,而 Alice 不知道 Bob 能够恢复哪个输入键。乱码表现在处于以下状态:
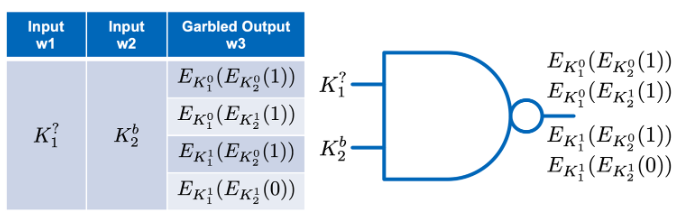
Bob 知道这对输入键正好解锁了一个乱码输出条目,但由于他不知道 Alice 的键对应于哪个输入位,他将不得不尝试解密所有四个条目。只有一个解密条目位于 {0,1} 中,而其他条目将显示为随机数。Bob 现在发布结果,以便 Alice 和 Bob 都了解函数的结果,而不必透露他们的私人输入。
乱码电路的应用
使用专用输入计算函数的问题称为安全多方计算(MPC)或安全函数评估(SFE)。乱码电路为许多不同领域的重要问题提供了解决方案,包括IP保护(在不知道功能是什么的情况下评估功能),医疗保健(分析而不披露医疗记录),生物识别(比较而不披露生物特征测量值),私有数据库即服务(托管和处理对处理器隐藏的客户数据的查询),基于云的机器学习(保护专有模型免受客户侵害, 以及来自处理器的敏感客户数据)等等!
审核编辑:郭婷
-
如何进行电源设计–第3部分2024-09-07 361
-
电源设计方法-第3部分2024-09-06 255
-
如何进行电源供应设计-第3部分2024-08-30 370
-
边缘智能第3部分:边缘节点通信2023-11-24 397
-
径向气流培养箱(第3部分)2023-06-16 443
-
使用Zio控制机械臂(第3部分)2022-12-30 543
-
看懂MOSFET数据表,第3部分—连续电流额定值2022-11-03 713
-
优化您的汽车USB电路防电池短路设计——第2部分2022-11-02 663
-
实时控制技术满足实时工业通信发展的需求——第3部分2022-10-31 443
-
用电信息采集系统通信协议第3部分2021-08-27 854
-
布局电源板以将EMI降至最低:第3部分2021-04-28 703
-
电动汽车传导充电用连接装置第3部分:直流充电接口2016-07-15 1050
全部0条评论

快来发表一下你的评论吧 !

