对1oo2架构的思考

IEC 61508-6：2010附录B分析了如何计算包括1oo2架构在内的几种架构的故障概率计算。在这种情况下，1oo2代表“二分之一”，这意味着有两个安全通道，每个通道的排列方式是，如果至少有一个通道跳闸，系统将进入安全状态。这通常比使用单个通道提供更高的安全性。我之所以这么说，通常是因为具有非常可靠组件和/或更高诊断覆盖率的单通道架构可以实现更低的PFH。

下面重绘了IEC 1-2：61508图B.6中2010oo6通道的框图。

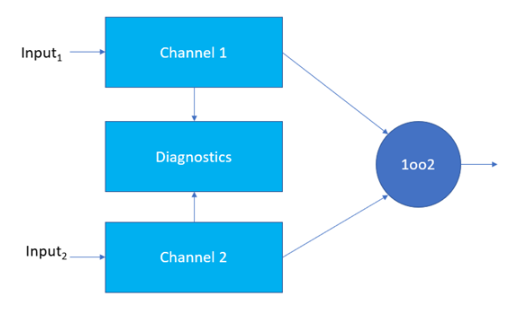
图 1 - 符合 IEC 1 标准的 2oo61508 架构

此图与 B.3.2.2.2 中的文本相匹配，其中指出“该架构由两个并联的通道组成，因此任一通道都可以处理安全功能。因此，在安全功能按需失效之前，两个通道都必须存在危险的故障。

包含 1oo2 文本的深蓝色方块是一个选民，为了清楚起见，我认为架构最好显示为如下所示的内容，否则投票本身就是击败冗余的单点故障。

此处的投票逻辑显示为两个开关。如果任一开关打开，则执行器或接触器的电源断开，从而使机器进入安全状态（断开电源通常称为基本安全措施）。

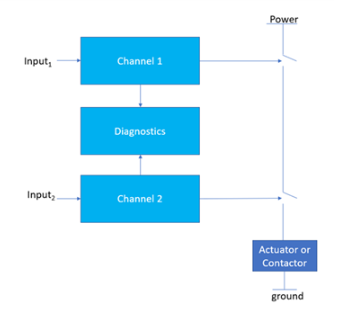
图 2 - 1oo2 重新绘制以清晰显示选民

在有人问为什么诊断没有第三个输出来控制额外的开关之前，文本清楚地表明“假设任何诊断测试只会报告发现的故障，不会更改任何输出状态或更改输出投票”，因此图表和文本是一致的。也可以将其更改为每个通道具有额外的诊断块，而不是共享诊断块，但这显然没有完成。正如我们稍后将看到的，方程假设相同的冗余（只有 DC 和 λ 的 1 个公共值的对于两个通道）。诊断可能是通过比较进行诊断，在这种情况下，当系统将进入安全状态时，您无法判断哪些通道出现故障。

我注意到 1oo2D 架构的每个通道都有一个诊断块，诊断确实会输入投票，但要小心，因为 IEC 1-2：61508 中绘制的 6oo2010D 架构实际上针对高可用性进行了优化，安全性更高，正如其描述所证明的那样，“在正常运行期间，两个通道都需要要求安全功能才能发生”。我见过其他文档和标准，它们对1oo2D有不同的含义。

IEC 1-2的图B.7给出了61508oo6架构的匹配可靠性框图。我在下面重新绘制了它。

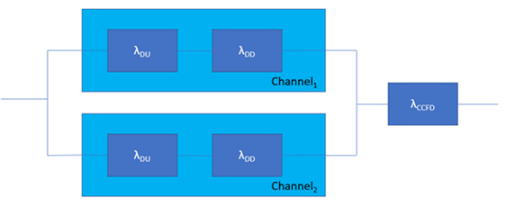
图 3 - 1oo2 架构的可靠性框图

可靠性框图是评估安全功能的PFH（每小时平均危险故障概率）的工具。在此图中，仅显示了每个通道的危险故障率和常见原因。

每个通道都可能危险或安全地发生故障，但可靠性框图上未显示安全或实际上没有影响的故障。相反，仅显示危险的未检测到的故障和检测到的危险故障，并用λ表示的和 λDD.此外，常见原因故障贡献与并行通道串联显示，其危险故障率由λCCFD.常见原因故障是导致两个通道同时发生故障的故障（对于两个通道中的随机故障，分别是不同的）。

如果您正在注意，您可能会问为什么包括检测到的危险故障。检测到这些故障，但该信息未在附录B中定义的1oo2架构中使用，因为它明确指出“假设任何诊断测试只会报告发现的故障，不会更改任何输出状态或更改输出投票。我觉得这是不寻常的，如果您的系统实际上有办法进入安全状态以应对检测到的危险故障，这将使生成的方程变得保守。

从 1oo2 架构的描述中不清楚，但是我们稍后将研究的方程式清楚地表明，检测到的故障以某种方式标记给修复团队，该团队将及时修复检测到的错误 MTTR。在进行这些维修之前，系统使用良好的通道以较低的完整性运行。与诊断程序具有自己的输出以使系统进入安全状态相比，这提供了更高级别的可用性。

我注意到该方程没有对诊断的故障率进行建模，但这甚至不包括在 1oo1 系统的计算中，至少对我来说，目前还不清楚诊断失败是否对应于根据 IEC 61508 的安全功能的危险故障，并且根据 IEC 2 修订版 61508 对它们进行建模的要求仅限于附录 D 中的声明第 2 部分说安全手册必须包含诊断的故障率。无论如何，我跑题了，让我们回到等式。

我们现在从IEC 61508第6部分的低需求部分跳到B.3.3.2.2中的高需求部分，我们找到下面的等式。

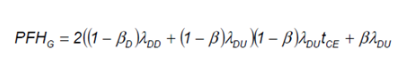
图 4 - 1oo2 架构每小时发生危险故障的平均概率

该等式包括

BD– 导致两个通道同时发生故障的检测到的故障比例。典型值为 0.01、0.02 至 0.1。

β – 导致两个通道同时失败的所有故障的比例。典型值与β相似。

LDD– 每个通道检测到的危险故障率。数值通常在 1e-6 到 1e-9/h 的范围内。

L的– 每个通道的危险未检测到故障率。数值通常在 1e-6 到 1e-9/h 的范围内。

TCE – 见下文

t的定义那在 1oo1 部分中给出，如下所示，所以让我们从它开始。

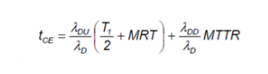
图5 - 通道等效停机时间

这里有一些新术语：

T1– 验证测试间隔，如果没有验证测试，则说明安全系统的预期使用寿命。T1以小时为单位给出，其中一年为 8760 小时。

MRT – 平均维修时间（小时）

MTTR – 平均恢复时间（小时）

MRT和MTTR都是维修时间，但一个适用于通过验证测试检测到的故障，其他适用于通过自动测试（即正常诊断）检测到的故障。

所以，让我们从 t 开始那它由两部分组成。

第一部分那方程表示任何自动诊断都无法检测到的危险故障的比例。如果执行非自动测试（证明测试），则假定这将检测自动测试未检测到的故障，并且平均而言，这些故障对于 T 已经存在1/2+实施修复的时间。在实践中，T1通常等于系统的预期寿命，因为从未完成过证明测试。在这种情况下，故障平均存在一半的生命周期。当通过验证测试检测到故障时，将在MRT中进行修复。

后半段那方程表示检测到的危险故障，一旦检测到，它们将在 MTTR 中修复。在实践中，您可能会设置 MRT=MTTR=0，假设维修时间与系统的使用寿命相比更快（海上风电场或太空应用可能无法从此假设中受益）。在停机并等待修复时，系统依赖于另一个通道正常工作。

所以现在让我们回到主要等式。

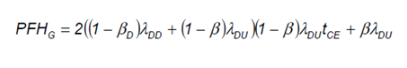
图6 - 重复标准中的公式

让我们先看等式的最后一点。βλ的= λCCFD从可靠性框图。β的典型值为 1%、2%、5% 或 10%。如果 β=10%，则 PFHG 通常是单个通道的危险未检测到故障率的 10%，即通道的可靠性（在安全意义上）提高了 10 倍。如果没有等式的这一部分，你会天真地认为FIT率提高了100倍，1000倍甚至更多。

等式的第一部分表示未检测到的故障的累积，平均而言，对于 T 将存在这些故障1/2 其中 T1是验证测试间隔或安全系统的使用寿命，以较小者为准。要看到这一点，让我们设置 MTTR=MTR=β=βD=0。然后，方程的第一部分变为 PFHG = 2*λ的2*吨1/2其中 λ的2表示两个完全独立的项目发生故障的概率，并且包括前 2 个，因为有两种方式可以先发生通道 1 故障，然后通道 2 发生故障，反之亦然。The T1最后/2来自这样一个事实，即如果存在故障，则平均存在 T1/2（记住每小时危险故障平均概率的PFH标准）。

如果您想了解方程为输入变量的各种值给出的结果，后续表 B.10 到 B.13 给出计算出的 PFHG适用于各种架构，如 λD、直流、β、MTTR 和 T1假设βD=b/2。

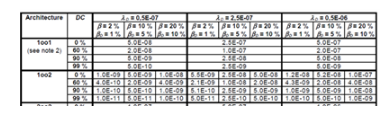
图 7 - IEC 61508-6：2010 中的一些预先计算值

将等式分解为多个部分，看看等式的哪个部分占主导地位是很有趣的。

验证测试间隔为 20 年， MTTR=MTR=0， β=0.02， λD=50 等式的第一部分是 DC=20% 时最大值<总数的 60%，并且随着 DC 的增加而迅速变得不那么重要。

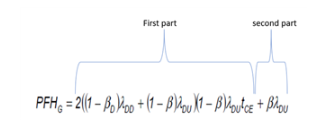
图8 - 零件方程

一旦证明测试间隔下降到10年或更短，方程的第一部分就变得微不足道了。

当 Beta 降低到 2% 或更低时，等式前半部分的影响变得更加显着，但对于 β 的最小可行值来说，仍然不到总数的 30%，这对我来说是违反直觉的。我必须试着找时间再次玩这个等式。

至于这个等式从何而来，我不知道。但是我看过一些关于类似方程的论文，摘录如下所示。我曾尝试使用马尔可夫模型和符号数学程序为自己推导它，但在我弄清楚如何在数学软件中进行部分集成之前失去了耐心。下面是我看到的一个推导的中间部分，显示了推导中的步骤 95 到 98，因此您需要良好的数学知识和大量时间来从第一原理验证此方程。

图 9 - 方程背后的计算示例

审核编辑：郭婷