教你如何利用verilog轻松实现高分辨率DDS

DDS基本原理

1.原理框图

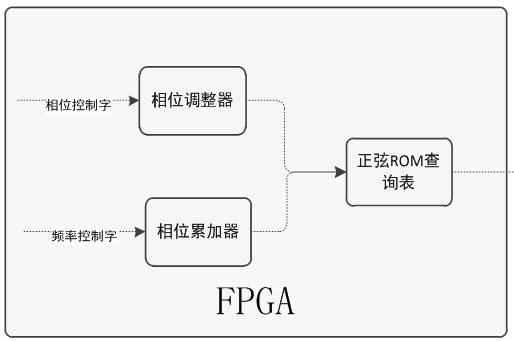
图1. FPGA产生DDS框图

上图就是DDS的的FPGA实现框图，完整的DDS还应该在外面有DAC和低通滤波器的，然而很多时候我们是不需要这两个的，因为上图的DDS输出的信号就在数字域，凡是数学域的信号都可以用它参与处理了，所以正弦ROM查找表出来后的信号可以直接给到其他的逻辑使用。只有要在模拟域参与处理才会把DDS的数字信号用DAC和低通滤波变换成模拟信号。

2.DDS正弦波产生原理

正弦ROM查找表里面就是按地址存放的一个周期的正弦波，可以根据幅值精度要求分成256，1024，等点数，点数越多，波形越精细，越接近真实的模拟正弦波。但是由于FPGA资源有限，选择一个能够满足要求的点数就足够了。

相位调整器是控制输出波形的初相位，也就是波形输出起点从哪里开始。

相位累加器是控制ROM地址跳变的。相位累加器在每个时钟脉冲输入时，把频率控制字累加一次，相位累加器的输出数据就是信号的相位，也就是ROM的地址。由于相位累加器字长的限制，相位累加器累加到一定值后，其输出将会溢出，这样波形存储器的地址就会循环一次，即意味着输出波形循环一周。故改变频率控制字即相位增量，就可以改变相位累加器的溢出时间，在时钟频率不变的条件下就可以改变输出频率。改变查表寻址的时钟频率，同样也可以改变输出波形的频率。

也就是说通过相位调整器和相位累加器就可以控制你输出波形的相位和频率！

DDS实例说明

1.16点DDS举例

下图是一个16点的DDS ROM存取示意图，横轴是二进制的ROM地址，纵轴是每个地址对应的幅值。

如果频率控制字K=1，相位控制字是0，那么ROM输出就是从0开始+1，一直到15再次归0，如此循环。如果DDS工作时钟是Fc，那么这种情况下，输出正弦波频率Fout就是Fc/(2^4)=Fc/16。如果K=2，输出则是一半的时间就输出完成整个周期所以是Fc/(2^4)*2=Fc/8。以此类推可以得到如下公式，N是ROM地址位宽，也就是频率控制字的二进制位宽：

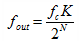
......公式1

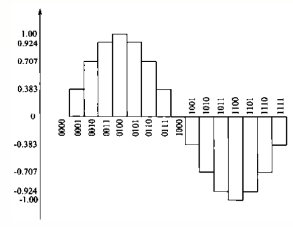
图2. DDS输出 波形示意图

频率分辨率，也就是频率控制字每变化1，频率变化的大小，公式如下：

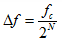
......公式2

本质上也就是K=1和0的时候的输出频率之差，这个计算起来是最简单的。

2.提高频率分辨率的方法

根据公式2我们可以得到：N越大，也就是频率控制字位宽越大，那么分辨率越高，我们设置的任意频率都可以做到更接近，频谱上就越看不出差别。而且我们可以知道，这和输出波形的位宽是无关的，输出位宽只和幅值精度有关。也就是说，我们可以用一个ROM存1024个点，每个点16bit精度，但是频率控制字是32bit，累加结果只用最高10bit，这样，就可以让ROM存储少，但是频率分辨率确很高。这种方法在实际中也是很实用的方法。

仿真结果说明

如下图所示，rst为高电平时复位整个模块，en为高电平整个模块才会工作，dout_vld为高电平的时候输出数据才是有效的点。所以输出可以根据dout_vld为1的时候打印到文件里面，用matlab分析频谱。由于输出数字信号一定是离散的所以一定会有高频分量，只是占比多少的问题，后面的模拟滤波器如果设置合理是可以把基频分量取出来的，这样就可以实现DA功能。DDS输出频率越高，三角函数畸变也就越严重，但是实际处理过程中往往不需要他的波形多么接近正弦波，只要频谱的谱线足够干净就可以。详见下一节MATLAB分析。

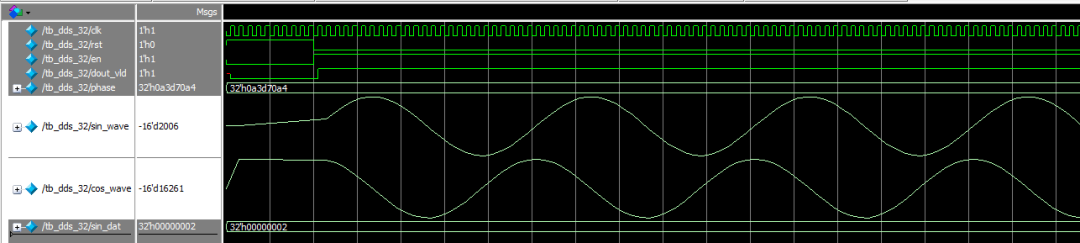
matlab结果说明

tb默认设置DDS工作在100M时钟下，产生4M正弦波，输出2048点后用这些点去做FFT，结果如下图所示，结果显示正弦波频率是4.035M，和理论预测相差35KHz，准确度为0.875%。然而按照32bit的位宽精度应该比这个精确的多的。那么为什么会有这种差距呢？原因是100M的采样率，1024点FFT分辨率只有0.1M左右，远远大于DDS的输出频率分辨率，所以，即便DDS输出频率很准确，FFT也不会认为有那么准确，必须要FFT分辨率大于DDS分辨率的时候才能准确的计算出DDS的频谱。

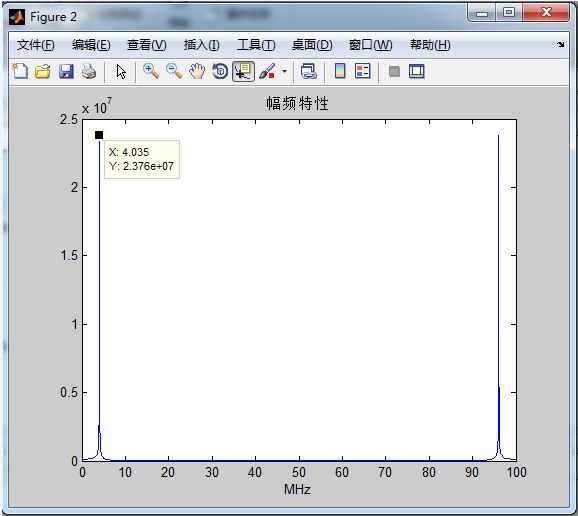
那么按照以上理论，只需要提高FFT点数，DDS的结果应该更接近理想结果，于是我们输出131072点之后我们做FFT，结果如下：

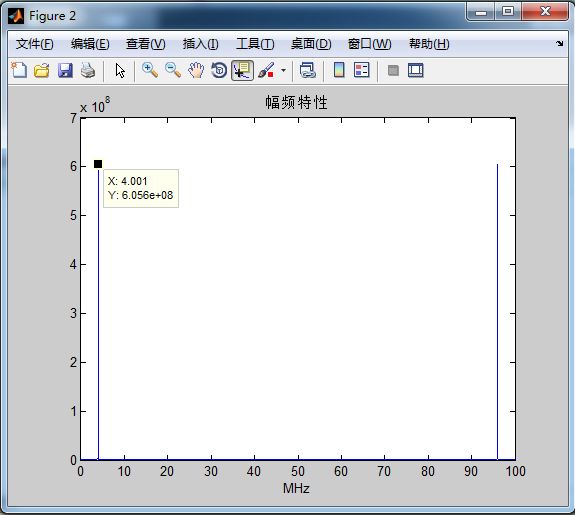
频谱显示为4.001MHz，准确度为0.025%，确实比2048点精准了很多倍。然而这里的FFT分辨率其实还是不够的，只不过输出太多点数需要花时间，有兴趣的读者可以继续增大点数看看分辨率究竟有多高，可能会让你吓一跳哦！

这里其实也体现了DDS的优点，输出频率精度非常高，而且相位稳定可靠，消耗资源又少！