

产生振荡器的Barkhausen准则
描述
Kuo-Chang和Marie-Eve Carre
我们什么时候有放大器或振荡器?
在设计放大器时,我们都面临着看到它不稳定并改用振荡器的风险。反之亦然:当试图设计振荡器时,人们观察到我们可以得到完全“静音”的东西。这两个功能之间显然存在无形的障碍。说放大器有时或总是可以充当振荡器,反之亦然是正确的。这种障碍通常是由反馈循环决定的。其强度可以决定哪个行为、放大器或振荡器。这取决于设计师的技能,以确保他们将生成哪一个。在本博客中,我们将选择从“正确”反馈的放大器开始设计振荡器的角度。
什么是巴克豪森标准?
为了更新我们的高中或大学课程,Barkhausen准则用于设计正确数量的反馈,以确保电路将成为振荡器并提供所需的频率。
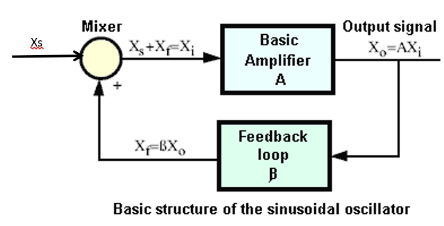
为了说明Barhausen准则,让我们使用一个具有相移反馈β(复数)的经典放大器(纯增益A)。选择A和β模块中的元件是为了确保输出和输入之间的n*2*π(n是整数值)相移,以实现完整的正循环。在这种情况下,生成的输出强制执行原始输入并使系统不稳定。巴克豪森准则给出了所需的频率和最小增益。建立该条件非常容易:
可以观察到 Xo = A.Xi = A. (Xs+Xf) = A. (Xs + β.Xo),因此:
Xo = A .Xs / (1-A.β)
由于振荡器中没有输入:如果 1-A.β 也是 0,Xs=0 和 Xo 可以(最终)存在(我们有一个典型的 0/0 情况,它是“不确定的”(可能是 0、∞ 或者希望介于两者之间......
1 – Aβ = 0 是Barkhausen标准或条件。
或 1 – A (βr + j βi) = 0 ;因为β是一个复数
因此,在Barkhausen关系中隐藏了2个方程:
虚部等于 0:βi = 0 这给出了频率
实数等于 0:1 = A。 βr 这给出了增益
如何应用Barkhausen标准?
让我们考虑以下相移正弦波振荡器;可以看到由运算放大器安装的放大器部分作为经典反相方案,增益 = -R2/R1。然后,我们有了由3个串联的缓冲RC电路制成的反馈部分。每个电池确保 0° 至 90° 相移。由于放大器已经确保 -180° 偏移,我们最终将得到可能超过 360° 的全局偏移;确保强烈的“不稳定性”。
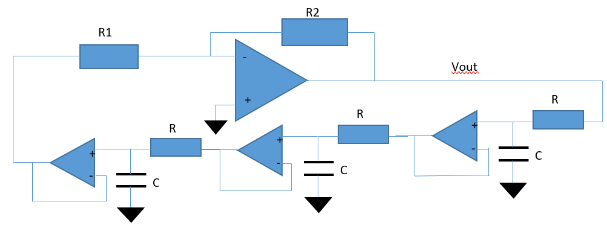
然后反馈电路(β)立即计算为:
β = [1/(1 +jωRC)]。[1/(1 +jωRC)]。[1/(1 +jωRC)] = 1/(1+jωRC)3
通过开发和的立方体 (即( a+b)3 = a3 +3a²b + 3ab² + b3):
β = 1 / (1 + 3 (jωRC) + 3(jωRC)² + (jωRC)3)
β = 1 / (1 + 3jωRC - 3ω²R²C² - jω3R3C3)
Barkhausen准则的第一个方程说β的虚部必须是 0;因此,可以提取振荡器频率:
3ωRC - ω3R3C3 = 0 或 ω²R²C² = 3 或 ω = √3/RC 弧度/s = √3/(2πRC) Hz;知道R和C,得到振荡器频率
Barkhausen准则的第二个方程说:1 – Aβr = 0 或 βr = 1/A 或 A=1/βr
在我们的电路中,βr = 1/(1-3ω²R²C²),由于根据前面的公式ω²R²C² = 3,我们将得到:
βr = 1/(1-3x3) = 1/(-8) = -1/8 增益 A 为 -8,与值 R 和 C 无关
总而言之,应用于电路的Barkhausen准则仅为:ω²R²C² = 3和A = -8;这是放大器为确保和维持振荡而必须提供的最小(绝对)增益。
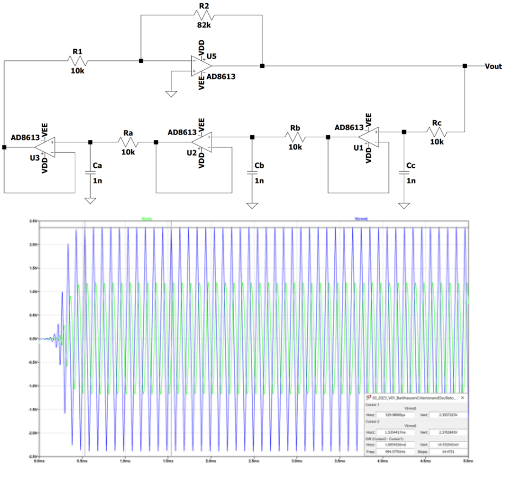
仿真结果:
得益于Marie-Eve Carre的支持,第一次尝试只是快速随机选择一个运算放大器(AD8613)并使用LT-Spice进行仿真。我们有振荡,但获得的频率并不完全是计算的频率。将对运算放大器特性的影响进行更精确的分析。
结论:
Barkhausen准则可用于设计具有增益级和反馈级结构的振荡器。反馈方程将给出振荡频率,正向级将固定放大器必须提供的最小增益。
审核编辑:郭婷
-
振荡器,振荡器的分类,振荡器的特性2010-03-08 1537
-
基本哈特利振荡器设计2023-06-01 2296
-
什么是RC振荡器?RC振荡器的工作原理 基本RC振荡器电路设计2023-08-31 7337
-
石英振荡器热拍频率的产生2008-11-24 641
-
振荡器,振荡器是什么意思2010-03-08 9610
-
振荡器,振荡器的分类和原理是什么?2010-03-22 19067
-
压控振荡器,压控振荡器是什么意思2010-03-22 5321
-
CMOS振荡器设计2011-06-15 11060
-
振荡器自生振荡分析之反馈理论与barkhausen准则2016-09-06 4542
-
振荡器的类型有哪些2023-11-15 1670
-
晶体振荡器与LC振荡器的区别2023-12-15 2657
-
正弦波振荡器产生自激振荡的条件是什么2024-02-09 4519
-
皮尔斯振荡器的工作原理 皮尔斯振荡器电路详解2024-02-26 3016
-
从晶体振荡器产生时钟信号2024-09-18 129
-
压控振荡器vco工作原理是什么2024-09-25 1797
全部0条评论

快来发表一下你的评论吧 !

