S-function详解与模型参考自适应仿真案例

1前言

S-Function是system-function系统函数的缩写，是指采用非图形化的方式描述的一个功能块。S-Function提供给用户自己编写程序来满足自己要求模型的接口。

2 s-function总体架构

S-function包括主函数和6个子函数，子函数包括

1.mdlInitializeSizes（初始化）

2.mdlDerivatives（连续状态微分）

3.mdlUpdate（离散状态更新）

4.mdlOutputs（模块输出）

5.mdlGetTimeOfNextVarHit（计算下次采样时刻）

6.mdlTerminate（仿真结束）。

2.1 s-function 执行过程

1. 在仿真开始时，执行mdlInitializeSizes
2. 若系统包含连续部分，则调用mdlDerivatives；若系统包含离散部分，则调用mdlUpdate
3. 调用mdlOutputs，产生输出
4. 若满足条件，则执行mdlGetTimeOfNextVarHit
5. 循环执行1--3，直至仿真停止
6. 执行mdlTerminate，仿真停止

2.2 s-function 输入输出参数与状态变量

function [sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag)

S-function是基于状态空间表达式而设置的仿真模块，需要了解这个仿真模块的输入输出和内部的状态变量。

输入变量：

t ：系统时间

x ：系统状态

u ： 系统输入，即在simulink models中连接至S-function的线上的数据。注意区分x和u

flag ： 系统状态，由系统自动生成，决定了系统应当执行哪个S-function子函数

除了这四个必须有的变量，还可以自行根据需要添加变量，供子函数调用

输出变量：

sys ： 系统本身，可以理解为下一时刻的系统；同时sys的前几个数值（sys[1]等)是系统的输出，即在simulink中S-function伸出线上的数据

x0 ： 系统初始状态

str ： 状态排序字符串，通常指定为[]。

ts ： 可认为是采样时间

（simStateCompliance 不用管）

3 子函数

3.1 mdlInitializeSizes函数

function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes

% 不需要更改的内容
sizes = simsizes;

% 需要更改的内容：状态、输出、输入的数量
sizes.NumContStates = 0; %连续状态的数量
sizes.NumDiscStates = 0; %离散状态的数量
sizes.NumOutputs = 0; %输出的数量
sizes.NumInputs = 0; %输入的数量
sizes.DirFeedthrough = 1; %输出y和输入u是否是直通（输出的向量中是否直接含有输入）
sizes.NumSampleTimes = 1; %采样时间

sys = simsizes(sizes);

% 需要更改的内容：状态变量的初始值
x0  = [];

% 不需要更改的内容
str = [];

% 按需要更改，ts的第一个数字表示采样时间，第二个数字表示偏移量；连续系统不需要改
% [0 0]——表示默认采样时间（默认为0.2秒采样一次）；
% [-1 0] ——表示根据连接模块的采样频率进行采样；
ts  = [0 0];

% 按需要更改
simStateCompliance = 'UnknownSimState';

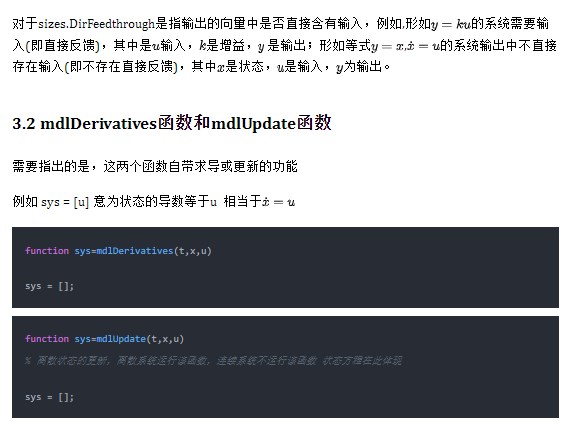
3.3 mdlOutputs函数

function sys=mdlOutputs(t,x,u)

sys = [];

3.4 mdlGetTimeOfNextVarHit函数

function sys=mdlGetTimeOfNextVarHit(t,x,u)
% 计算下一个采样点的绝对时间，只有当在mdlInitializeSizes中指定了变步长离散采样时间时，才使用该程序
sampleTime = 1;    %  Example, set the next hit to be one second later.
sys = t + sampleTime;

3.5 mdlTerminate函数

function sys=mdlTerminate(t,x,u)
% 终止函数，可添加当Simulink终止时所需执行内容

sys = [];

4 举例

4.1 二阶模型

对于如下被控对象，其传递函数为：

仿真结果：曲线重合，三种模型表达方式相同

4.2 简单自适应控制系统(MRAC)

4.2.1 系统模型与证明

s-function input

function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 2;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 3;
sizes.NumInputs      = 0;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0  = [0.5,0];
str = [];
ts  = [];

function sys=mdlDerivatives(t,x,u)
r=sin(4*t);
nmn1=10;
nmn2=25;
sys(1)=x(2);
sys(2)=-nmn1*x(2)-nmn2*x(1)+nmn2*r;

function sys=mdlOutputs(t,x,u)
r=sin(4*t);
nmn1=10;
nmn2=25;
xm=x(1);
dxm=x(2);
ddxm=-nmn1*x(2)-nmn2*x(1)+nmn2*r;
sys(1)=xm;
sys(2)=dxm;
sys(3)=ddxm;

s-function controller

function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 1;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 2;
sizes.NumInputs      = 6;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 0;
sys = simsizes(sizes);
x0  = [0];
str = [];
ts  = [];

function sys=mdlDerivatives(t,x,u)
xm=u(1);
dxm=u(2);
ddxm=u(3);
x1=u(4);
dx1=u(5);
e=x1-xm;
de=dx1-dxm;
nmn=6;
s=de+nmn*e;
v=ddxm-2*nmn*de-nmn^2*e;
gama=0.5;
sys(1)=-gama*v*s;

function sys=mdlOutputs(t,x,u)
xm=u(1);
dxm=u(2);
ddxm=u(3);
x1=u(4);
dx1=u(5);
e=x1-xm;
de=dx1-dxm;
nmn=6;
mp=x(1);
ut=mp*(ddxm-2*nmn*de-nmn^2*e);
sys(1)=mp;
sys(2)=ut;

s-function plant

function [sys,x0,str,ts]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 2;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 3;
sizes.NumInputs      = 2;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0  = [0.5,0];
str = [];
ts  = [0 0];

function sys=mdlDerivatives(t,x,u) 
m=2;
ut=u(2);
sys(1)=x(2);
sys(2)=1/m*ut;

function sys=mdlOutputs(t,x,u)
m=2;
sys(1)=x(1);
sys(2)=x(2);
sys(3)=m;

理想位置输出与真实位置输出

参数m估计值与真实值