基于数学模型用Matlab-simulink进行建模仿真验证

近期对永磁同步电机（PMSM）的控制方法做了一些学习与总结，由于涉及的内容较多，打算分几篇笔记分享出来，主要是对SVPWM控制算法的理解和基于数学模型用Matlab-simulink进行建模仿真验证。

1、简介

目前国内外关于永磁同步电机的界定是根据定子电流波形对无刷直流电机（BLDCM）与永磁同步电机（PMSM）进行界定，将电流波形为梯形波或者方波的无刷电机定义为BLDCM，将电流波形为正弦波的无刷电机定义为 PMSM。

SVPWM(矢量脉宽调制)是目前对PMSM的一种控制策略，基本思想就是通过逆变桥的不同开关模式控制电机，使产生的电压/电流/磁链轨迹尽可能逼近理想圆，使得电机的运转具有比较理想的性能。

概念如图，当一个点在空间内匀速做理想圆运动，那么在时域上产生的波形就是正弦，当然也可以逆过来理解，正弦波在空间上的轨迹就是一个圆，当时域上运动的离散点轨迹越密集，空间上的运动就越趋近理想圆。

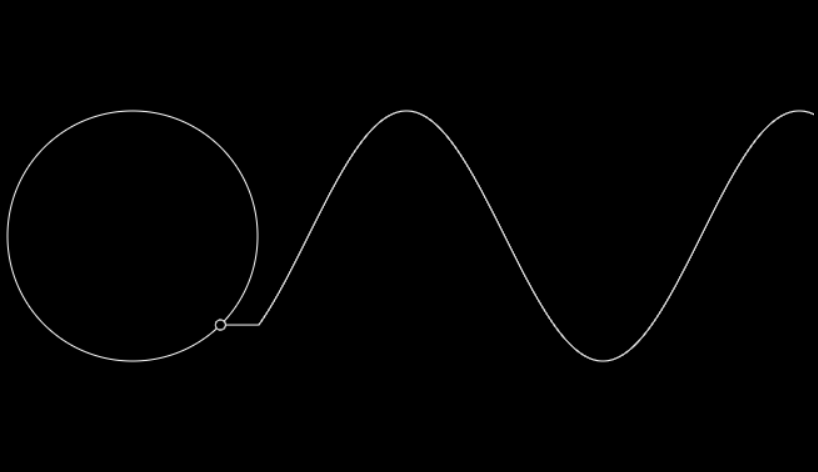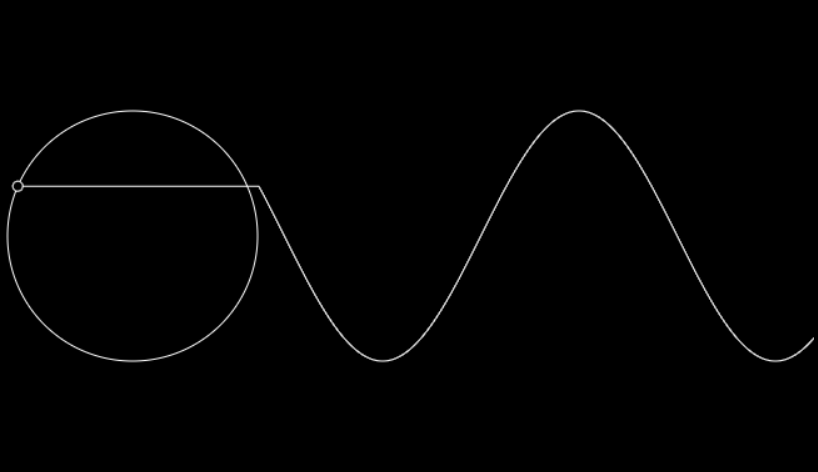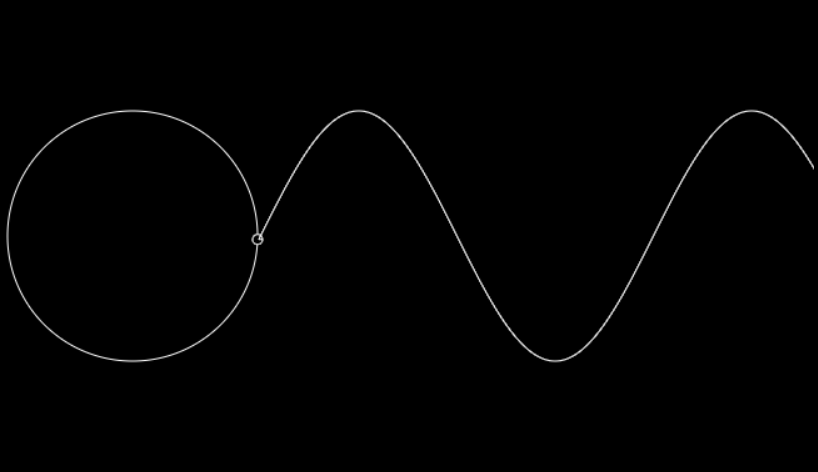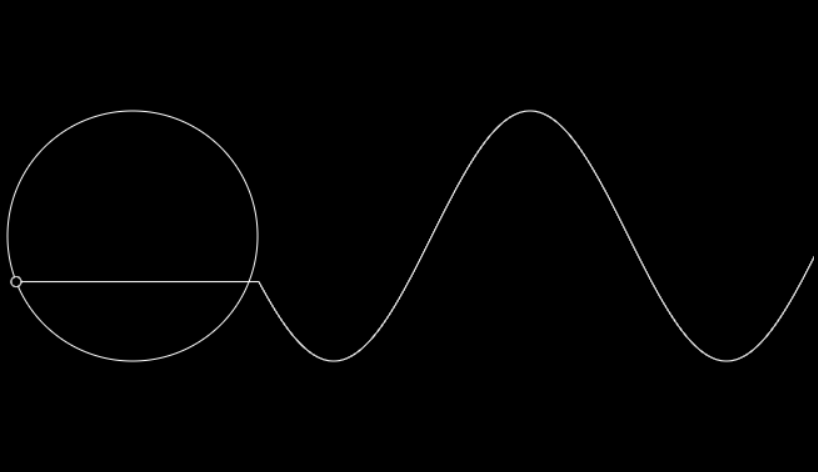
2、逆变桥与电机原理

对于两电平的三相逆变桥臂，如下图直流侧的电压为Udc，对于a、b、c三相桥臂，每个桥臂均有上下两个开关管（如MOS），上下管不能同时导通。为了方便控制计算，通常定义一组上管或一组下管的开关为1/0,根据A、B、C三相桥臂的开关状态，利用三位的二进制编码，可以组合出8种状态。

在真实电机控制工况中，该逆变器是真实的元器件。通过控制这六个开关的导通和切断，配合左边的直流电压源可以在右侧三个电机定子相上产生所需要的正弦电压。（六个开关的开关状态是离散的，所以该算法很适合离散的数字系统）

如三相上管为（100）时，可算得；

求解得；

对于剩余的七对组合，可同理求出相电压以及合成电压如下表。

对于 三相同步发电机 ，举例如下图；在定子侧，定子绕组逆时针相隔120°排布。在转子上的励磁绕组中通入励磁电流，转子铁芯被磁化。当转子逆时针旋转时，旋转磁场将依次切割A、B、C相绕组，根据电磁感应定律，将在ABC绕组上感应出电动势，并且由于绕组相隔120°，感应电动势也相差120°，也就是我们熟知的三相对称电压。

对于同步电动机而言，它的工作原理与发电机正好相反：在定子ABC绕组上施加三相对称电压，从而在气隙中生成逆时针旋转的磁场。旋转磁场拖动转子磁极，克服静摩擦力后，转子将开始旋转。重点是如何控制定子三相电动势，使其能够产生标准的圆形磁场。磁场越圆，意味着电机控制精度越高。

3、SVPWM控制原理

对于空间矢量的脉宽调制，我主要是通过仿真建模的思路来讲解，要想使得逆变器输出三相正弦波，通常用的调制策略是；给定参考电压信号，通过调制PWM驱动开关管的导通与关断，使得ABC三相的输出电压趋近于参考的输入电压。

参考三相电压的瞬时表达式如下; 三相对称电压公式加到三相坐标系上就会合成相应的电压矢量，随着时间的变化该矢量逆时针旋转且幅值不变。这里就要构建起坐标系的概念，ABC是固定的三相坐标系，坐标系里面又各自分布着正弦量。

ABC空间上互相差120度，按照逆时针模式，A滞后B滞后C，ABC三个坐标轴上的量在时间上差了120，且A轴上的量超前B轴上的量超前C轴上的量，正弦量随着时间的变化，合成矢量也在不断变换。这里的坐标系起源于电机的定转子位置，示意图如下： 合成空间电压矢量表达式； 这个公式比较重要，这里就详细说一下，通过欧拉公式对表达式进行傅里叶级数的逆变换；

最终得到的式子就只有虚实轴上的两个分量，虚轴超前于实轴90度。这样原来三个方向上的量就可以用两个方向的量来表示得到的合成矢量。**这时****令实轴为α轴，虚轴为β轴。即我们所说的CLARK变换；

****Uα=Ua-1/2(Ub+Uc)

Uβ=sqrt3/2(Ub-Uc)

**Ualpha,Ubeta即为两相静止坐标系下的分量，对应坐标系如下图；

将三相电压代入经过运算可得；

** Uα超前于Uβ90度，幅值相等，但数学表达式幅值已经为原来三相电压的3/2倍，这显然是违背了物理量的规律的，所以在控制算法中通常会乘上一个补偿系数2/3去抵消这个倍数，称为 等幅值变换 。** （另外需要计算功率时要用到等功率变换，推导类似，不多赘述）

** 扇区划分 **

根据逆变桥的八个开关状态，可以得到六个基础的非零矢量与两个零矢量，非零矢量的幅值相等，均为 2/3Udc ，角度分别相差60°。因此将6个非零矢量的顶点连接起来，正好是一个正六边形，两个相邻的矢量与六边形的边构成一个等边三角形。一共有6个等边三角形，通常称它们为扇区。

而合成矢量在扇区中走过的轨迹，就是一个圆，而我们的相电压的峰值轨迹，就是六个扇区的内切圆，大家可以想象一下，我们用调制开关管生成的等效矢量轨迹点是离散的，矢量旋转一圈的时间中合成向量的次数越多，顶点的轨迹也就越平滑且越趋近于圆。

这里用第一个扇区内的矢量具体合成例子来讲解，根据秒平衡的原理；每一个扇区，选择相邻的两个电压矢量以及零矢量，都可按照伏秒平衡的原则来合成扇区内的任意电压矢量。

如图，如果合成这个电压矢量维持的时长是1S，其效果就等效于U4作用0.5S+U6作用0.5S所产生的矢量效果；

式子中的TPWM周期限制了分量作用的时间，所以圆外的区域是合成不了的；

调制度

由最大相电压的幅值就是六个扇区内切圆，我们可以根据三角公式计算出它的值，无论考不考虑等幅值变换，最终母线电压都是相电压的根号三倍，那么由线电压=Sqrt(3)*相电压，可以得出我们逆变桥的调制度=1，意味着理论电压利用率达到了100%。

最后用Mtlab-Smulink搭建出Clark变换；用正弦波产线模块给出三相互差120°的正弦波，幅值设定40V，频率50HZ；

经过坐标变换生成αβ轴上的两项正弦量，经过仿真波形正确，变换前后幅值一致；