通过ADC的过采样提高测量分辨率的方法

在大多数情况下，10位的分辨率就足够了。但在某些情况下需要更高的精度。采用特殊的信号处理技术可以提高测量的分辨率。 通过使用一种称为“过采样和抽取”的方法，可以实现更高的分辨率，而不使用外部ADC。此应用程序说明了该方法，以及需要满足哪些条件才能使该方法正常工作。

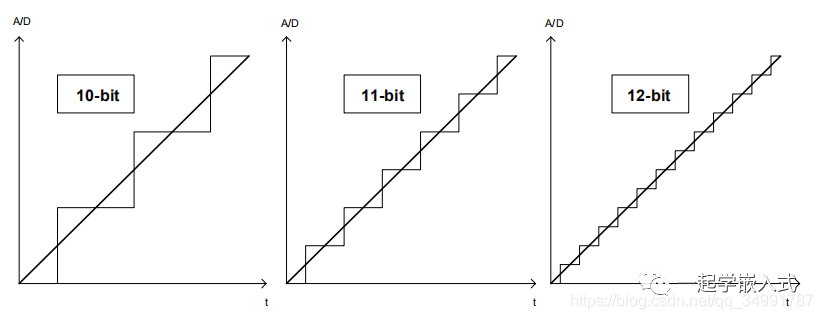
下面的例子和数字是为自由运行模式下的单端输入计算的。没有使用ADC降噪模式。这种方法在其他模式中也是有效的，尽管下面例子中的数字会有所不同。 ADC参考电压和ADC分辨率定义ADC步长。ADC的参考电压VREE可以选择为内部2.56V / 1.1V的参考电压AVCC或AREF引脚的参考电压。较低的VREE提供较高的电压精度，但最小化了输入信号的动态范围。

如果选择2.56V VREE，则在转换结果上给用户-2.5mV的精度，被测的最高输入电压为2.56V。或者，可以考虑使用ADC输入通道与增益级。这将给用户以ADCs动态范围为代价，以更好的电压精度测量模拟信号的可能性。 如果用动态范围来换取更好的电压分辨率是不可接受的，可以选择用信号的过采样来换取更好的分辨率。但该方法受到ADC特性的限制：使用过采样和抽取只会降低ADC的量化误差，而不能补偿ADC的积分非逼近性。

尼奎斯特定理指出，采样信号的速度必须至少是信号带宽的两倍，才能精确地重构波形；否则，高频内容将在感兴趣的频谱(通带)内的频率混叠。根据奈奎斯特定理，所需的最小采样频率为奈奎斯特频率。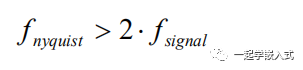



其中 fsignal 为输入信号中感兴趣的最高频率。fnyquist 以上的采样频率称为“过采样”。 然而，这个采样频率，只是一个理论上的绝对最小采样频率。在实践中，用户通常希望得到尽可能高的采样频率，以便在时域中得到被测信号的最佳表示。可以说在大多数情况下输入信号已经被过采样了采样频率是CPU时钟预调的结果;较低的预压因子可得到较高的ADC时钟频率。 在某一时刻，较高的ADC时钟会随着有效位元数(ENOB)的减少而降低转换的精度。

所有的ADC都有带宽限制，mcu ADC也不例外。 根据数据表，要得到一个10位分辨率的转换结果，ADC时钟频率应该是50kHz -200kHz。当ADC时钟为200kHz时，采样频率为~15kSPS，限制了被采样信号的上频率为~7.5kHz。根据数据表，ADC时钟可以驱动频率高达1Mhz，尽管这将降低ENOB。

“过采样和抽取”背后的理论是相当复杂的，但使用这种方法是相当容易的。这项技术需要更多的样本。这些额外的采样可以通过对信号进行过采样来实现。

对于每增加一比特的分辨率n，信号必须被过采样四次。

对输入信号采样的频率由下面公式给出。为了得到模拟输入信号的最佳可能的表示，有必要将信号过采样这么多。因为在平均时，更大数量的样本会给输入信号更好的表示。这将被认为是本应用说明的主要成分，并将通过下面的理论和例子进一步解释。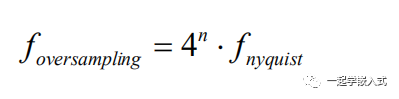



要使此方法正常工作，感兴趣的信号组件不应该在转换期间发生变化。然而，成功增强分辨率的另一个标准是，输入信号在采样时必须有所变化。 这看起来可能有些矛盾，但在这种情况下，变体仅意味着少量LSB。这种变化应该被看作是信号的噪声成分。

当信号过采样时，必须存在噪声以满足信号微小变化的要求。ADC的量化误差至少为0.5LSB。 因此，噪声振幅必须超过0.5 LSB才能切换LSB。1-2 LSB的噪声幅值更好，因为这将确保多个样本最终不会得到相同的值。噪声的标准，当使用抽取技术：

在转换期间，感兴趣的信号组件不应发生显著变化。

信号中应该存在一些噪声。

噪声的振幅应至少为 1 LSB。

通常在转换过程中会出现一些噪声。噪声可以是热噪声，来自CPU核心的噪声、IO端口的切换、电源的变化等。这种噪音在大多数情况下足以使这种方法工作。 但在特定情况下，可能需要在输入信号中添加一些人工噪声。这种方法称为抖动。

下图A显示了测量电压值介于两个量化步骤之间的信号的问题。对四个样本进行平均是没有用的，因为结果将是相同的低值。它可能只有助于减弱信号的波动。图B显示，在输入信号中加入一些人工噪声，转换结果的LSB会发生切换。增加四个这样的样本一半量化步骤，产生的结果给出了更好的输入值表示，如图C所示。ADC的虚拟分辨率从10位增加到11位。这种方法称为抽取，将在下面进一步说明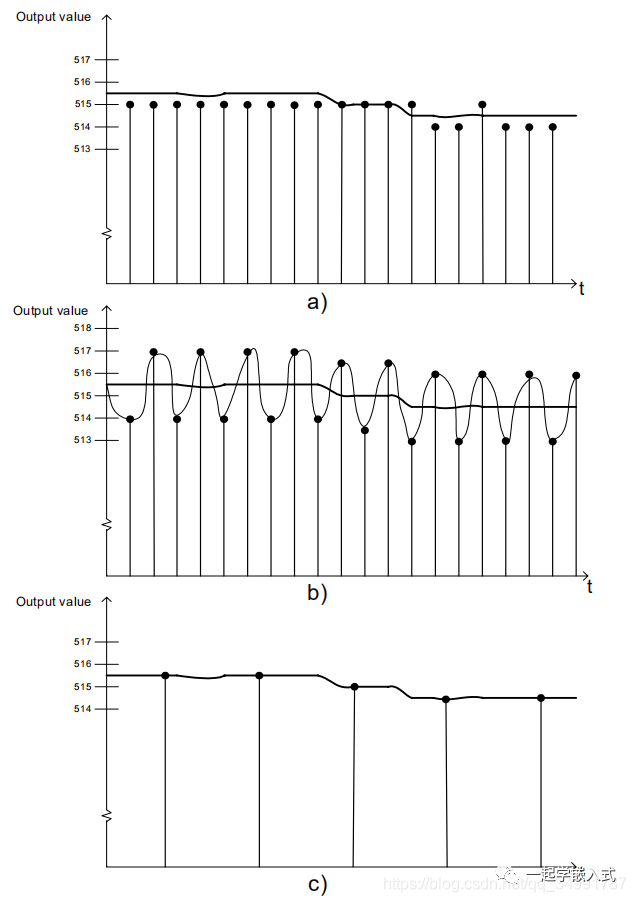



使用这种方法的另一个原因是为了提高信噪比。提高有效位元数(ENOB)将使噪声扩散到更大的二进制数上。噪声对每个二进制数字的影响减小。将采样频率加倍可以将带内噪声降低3dB，并将测量的分辨率提高0.5位。 均值的传统意义是将m个样本相加，然后除以m，称为正态均值。

平均ADC测量的数据相当于一个低通滤波器，具有衰减信号波动或噪声，平坦输入信号中的峰值的优点。移动平均法经常被用来做这个。 这意味着取m个读入值，将它们放入一个循环队列中，然后对最近的m个读入值进行平均。这将会有一点时间延迟，因为每个样本都是最后m个样本的表示。这可以在窗口重叠或不重叠的情况下完成。下面显示7 (Av1-Av7)，独立移动平均结果，不重叠。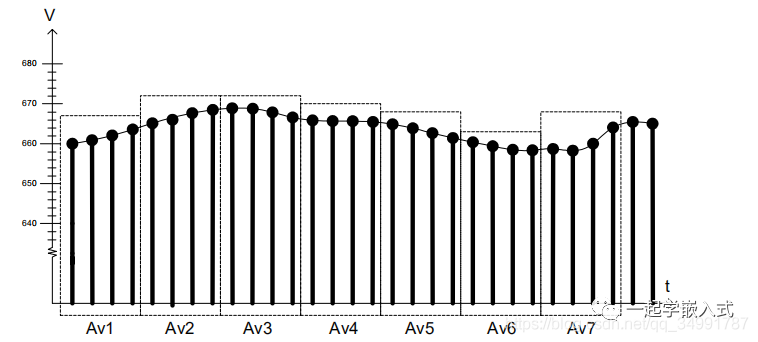



重要的是，要记住正常平均不会增加转换的分辨率。

抽取，或插值，是平均方法，结合过采样，以提高分辨率。 对信号进行过采样和低通滤波器的数字信号处理通常称为插值。在这个意义上，插值被用来产生新的样本，作为一个“平均”更大数量的样本。平均样本数越高，低通滤波器的选择性越强，插值效果越好。 通过对信号进行过采样得到的额外样本m被加起来，就像在日常取平均值中一样，但结果不像在日常平均值中一样除以m。

相反，结果是向右移动n，其中n是想要的额外的分辨率位，以缩放正确的答案。 向右移动二进制数一次等于二进制数除以2。从上面说到过的公式可以看出，将分辨率从10位增加到12位需要16个10位值的总和。16个10位值的和生成一个14位的结果，其中最后两位不期望包含有价值的信息。为了回到12位，有必要衡量结果。由式下图给出的标度因子sf是4个样本的和要除以的因子，以适当地标度结果。n是所需的额外比特数。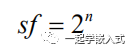



通常一个信号包含一些噪声，这种噪声通常具有高斯噪声的特征，通常称为白噪声或热噪声，被广泛的频谱识别，总能量在整个频率范围内平均分配。 在这些情况下，“过采样和抽取”的方法将工作，如果噪声的振幅足以切换ADC转换的LSB在其他情况下，可能需要在输入信号中加入人工噪声信号，这种方法称为抖动。

这种噪声的波形应该是高斯噪声，但周期波形也可以工作。这个噪声信号的频率取决于采样频率。经验法则是:“添加m个样本时，噪声信号的周期不应超过m个样本的周期”。 噪声的振幅应至少为1 LSB。在给信号添加人工噪声时，要记住噪声的平均值为零;过采样不足因此可能会造成偏移，如下图所示



点画线说明了锯齿信号的平均值。图A将引起一个负偏移。B将导致正偏移。在图C采样充分，避免偏移。为了制造人工噪声信号，可以使用计数器。由于计数器和ADC使用相同的锁源，这就提供了同步噪声和采样频率以避免偏移的可能性。 都柏林的一位酿酒大师想要测量他的酿酒厂的温度。一个缓慢变化的信号表示温度测量，其环境温度的标称电压为2.5 V。下图显示了该测温装置的特性。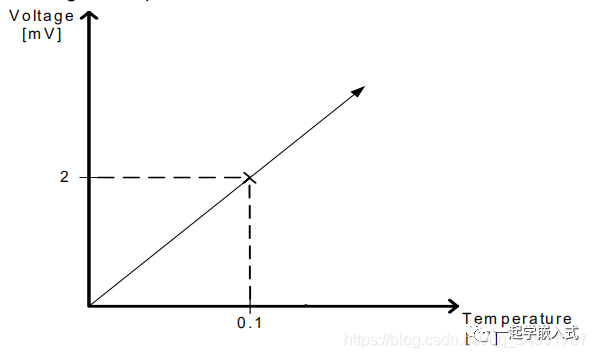



主机不想将输入信号的动态范围最小化，选择了一个5V的ADC参考电压。在这种情况下，10位ADC不能提供足够精确的转换结果。因为结果的 LSB 表示一个-5mV的'step'。这是不可接受的，因为这会导致结果可能高达0.25℃的偏差。 酿造主希望结果有0.1℃的精度，这要求电压分辨率低于2mV。如果测量用12位ADC表示，表示LSB的电压“step”将下降到~1.22mV。主机需要做的是将10位ADC转换为虚拟的12位ADO，输入信号变化非常缓慢。因此，不需要很高的采样频率。

  根据数据表，ADC时钟频率应在50kHz - 200kHz之间，以确保10位的有效分辨率。因此50kHz ADC时钟频率。然后采样频率变成-3800 SPS。在某一点，代表测量温度的直流值为2.4729V。下表给出了Vin=2.4729V和VREF= 5V时测量该值的不同分辨率选项。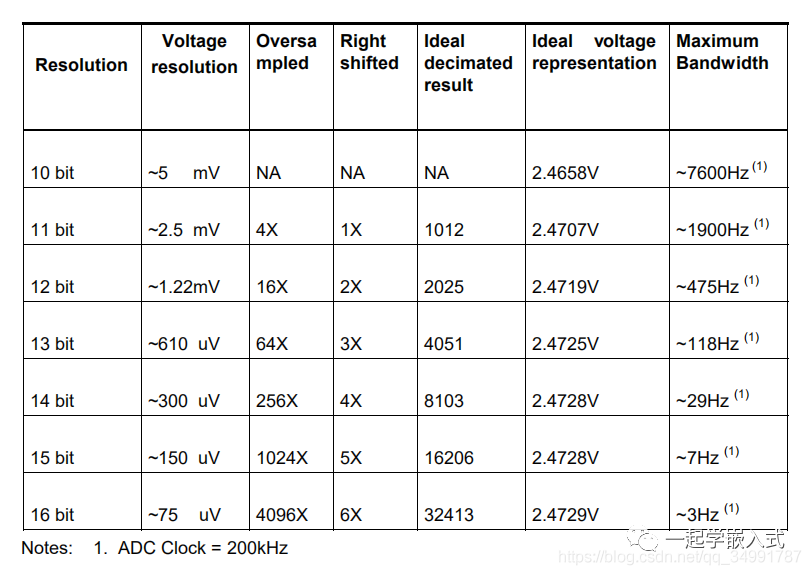



一次转换的结果是505，乍一看似乎是正确的。但是这个二进制数也对应于2.4683v。这使得用户不确定，并导致温度测量中的错误。在某些情况下，这可能是至关重要的。得出结论之前；信号通常包含足够的噪声，使抽取方法可行。 为了增加1位的分辨率，从相同的“邻域”添加了四个样本。

由于噪声的影响，这些样本的值之间存在一些LSB值的差异。 添加四个样品：508+ 507 + 505 + 505 = 2025。根据抽取原理，答案现在需要缩小到11位。它需要右移n次，n是额外的比特数。结果是1012。 提高分辨率后，突然之间就有可能实现原始量化步骤之间的采样。尽管如此，信号被过度采样以进一步提高分辨率，达到12位。添加16个10位的样本并右移结果2次就可以做到这一点。

结果是2025年。这个数字更可靠，因为使用一个12位的结果，误差范围减少到~1.22mV。 这个例子表明，开始时信号是慢变的，每秒采样3800 imes，电压精度为~5mV，现在每秒采样240个，分辨率为12位，电压精度为~1.22mV。 用户可能仍然希望通过平均16个12位样本(传统方法)来平衡信号波动。方法是将16个样本相加，然后除以16。最后，用户有15个SPS，平均16个12位相邻样本。 正常平均将减少随机噪声的后果，“过采样和抽取”将利用噪声来提高分辨率。

为了证明该方法的有效性，下面的例子将表明，不必使用外部ADC来获得更高的精度。信号发生器用于产生从OV到5V的线性斜坡信号。在“低噪音”环境中，信号发生器和控制器插在STK500板中，可能没有足够的噪音切换10位信号的最后几个位。因此有必要在输入信号中加入人为的“噪声”，使LSB开关。 将信号发生器产生的噪声直接加到输入信号上。用单片机产生噪声，使用PWM，并将其添加到输入信号当使用AVCC作为VREF时，添加由单片机生成的噪声到AREF当使用AREF作为VREF时，添加由mcu生成的噪声到AREF。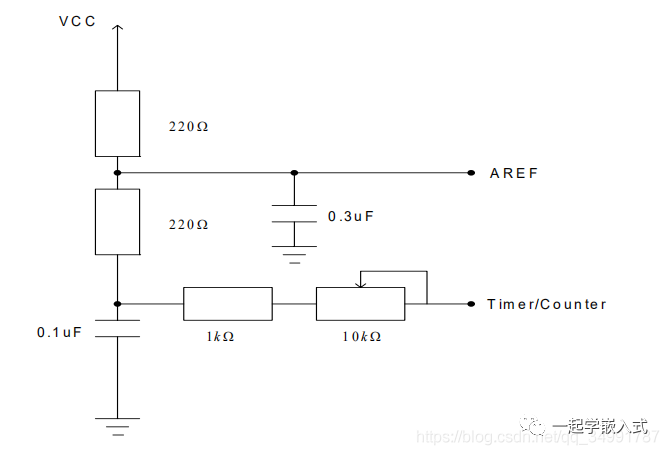



当VCC =5V时，滤波后的AREF引脚信号在计数器脉宽为0%时为2.5V，在计数器脉宽为100%时为5V。本例中pwm信号占空比为50%，基频为~3900Hz。10kS电位器是用来调整这种纹波。该PWM-信号要么作为参考电压的ADC在AREF，或作为噪声发生器连接到AREF引脚。 设AVCC为ADC参考电压。其思想是，在不干扰输入信号的情况下，参考电压的微小变化将产生与输入信号的微小变化相同的效果。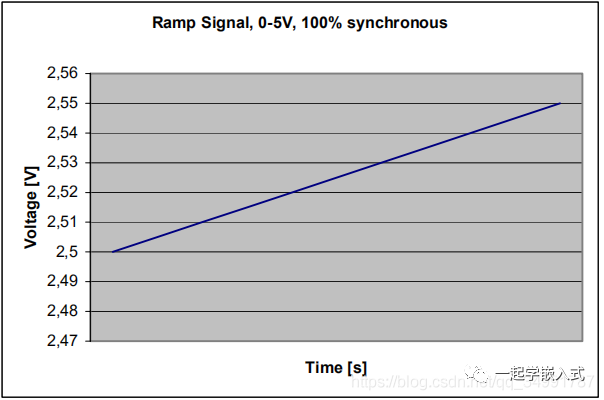





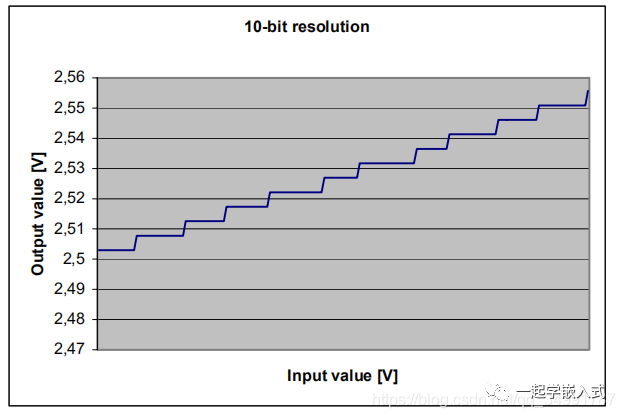
下图显示了当AREF为ADC参考电压时输入信号的12位离散表示，并且AREF加了一些LSB噪声。上面的公式，每个12位结果由16个10位样本组成。对ADC偏移量进行调整，根据应用说明，增益误差也需要调整。



以下图片显示了输入信号的14位离散表示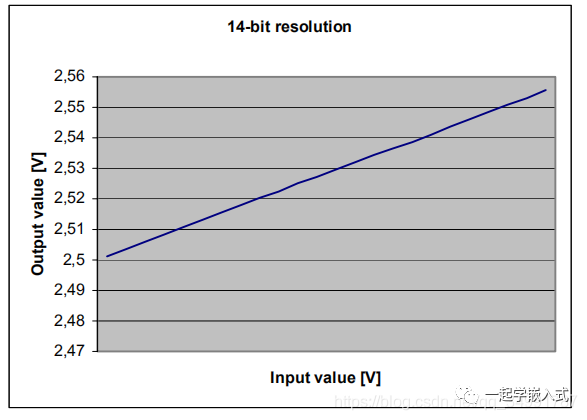



以下图片显示了输入信号的16位离散表示。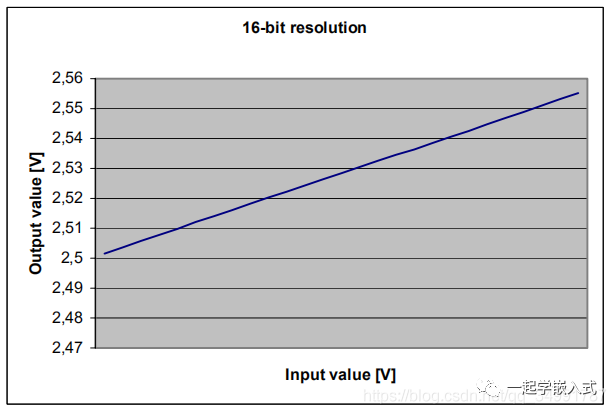



测量信号含有噪声时,或者当参考电压变化在这个例子中,重要的是要记住,顶部和底部值减少了相同的值作为噪声信号的振幅,给予轻微的减少被测信号的动态范围。在这种情况下，作为安全余量，偏移量被调整为100mV。 我们可以很容易地看到，通过使用过采样和抽取方法，有可能大大提高分辨率。

当ADC采样一个信号时，它对信号进行离散量化。这就引入了一些误差，通常称为量化误差。 正常平均只会均匀信号波动，而抽取会增加分辨率。在一个4 时间过采样信号，四个相邻数据点的平均值产生nev数据点。信号过采样的频率可由公式上面说过的公式计算。 加上这些额外的样本，然后将结果右移一个因子n。

产生分辨率增加n位的结果。平均四个模数转换器的结果得到一个新的模数转换器的结果是相同的，如果模数转换器采样率为14，但也有平均量化噪声的效果，提高信噪比。这将增加ENOB，减少量化误差。 随着更快的adc的可用性和低内存成本，过采样的优点是经济有效和可取的。

信号中必须存在一些噪声，至少1 LSB。

如果噪声幅度不够大，就给信号加噪声。

积累4个10位的样本，其中n是在分辨率中需要的额外比特数。

对累积的结果进行缩放，右移n次。

根据应用说明MCU补偿错误。看一下程序 ，此处ADC为10bit

 

#pragma vector=ADC_vect
__interrupt void ADCinterrupt(void)
{
  accumulator += ADC;//adc合   double
  samples++;//采样计数   short
}

  在这里进行采样和记录采样的次数，主要流程为 

 while(1)            // Eternal loop
  {
    if(samples>4095)  //如果到了过采样的临界点
      {
        oversampled();  //进行相应的过采样计算
      }
  }
  
void oversampled(void)
{
  __disable_interrupt();
  accumulator += 5150;   // 抵消误差补偿  这里可以用最小二乘法校正
  accumulator *= 0.9993;    // 增益误差补偿
  temp=(int)accumulator%64;   //做四舍五入
  accumulator/=64;   // 舍弃掉没用 这里除掉的是2的6次方，增加几位就是几次方
  if(temp>=32)
    {
      accumulator += 1;                
    }
  Vin = (accumulator/65536)*4.910;   //计算实际电压值
  samples     = 0;            
  accumulator = 0;            
  __enable_interrupt(); 
}

 

原文 ：https://blog.csdn.net/qq_34991787/article/details/107325006/  

 

 

审核编辑：刘清