阻抗变换之Norton Transformation

首先看下面的例子，下图是4个无源的网络，看起来是四个完全不同的网络，包括感值，终端阻抗，网络形式都不一样。

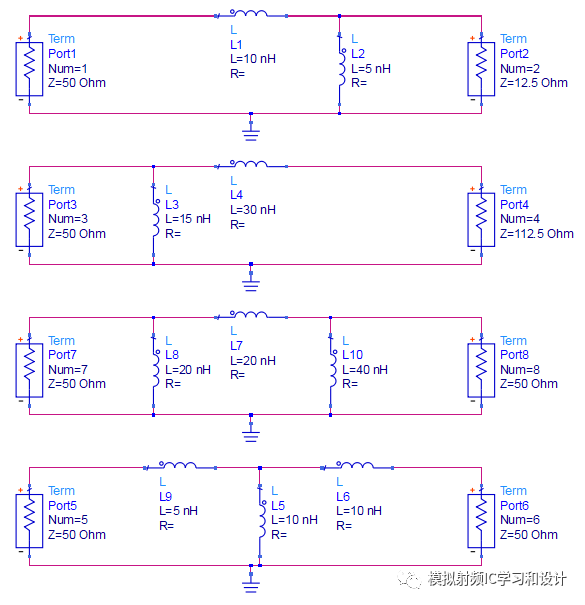
仿真看下这四个网络的S参数：

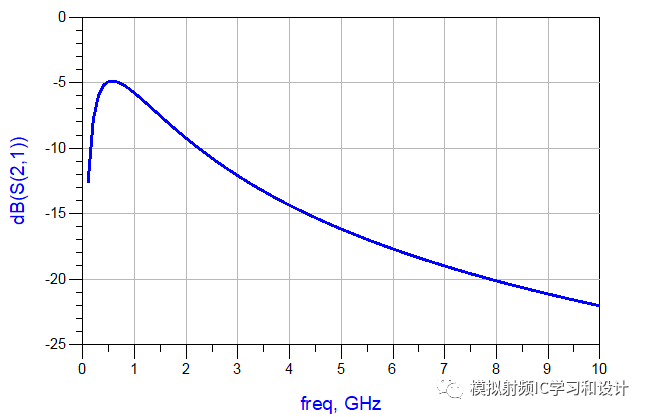
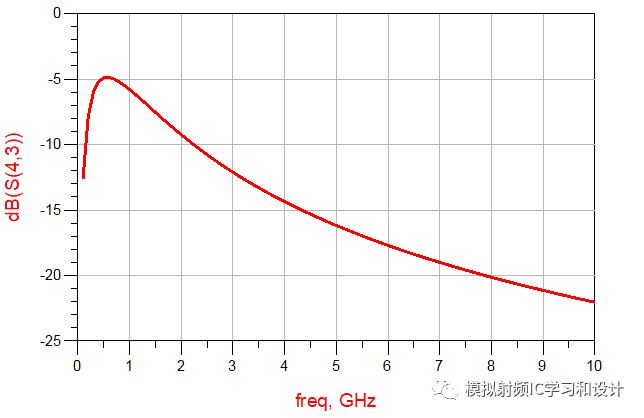
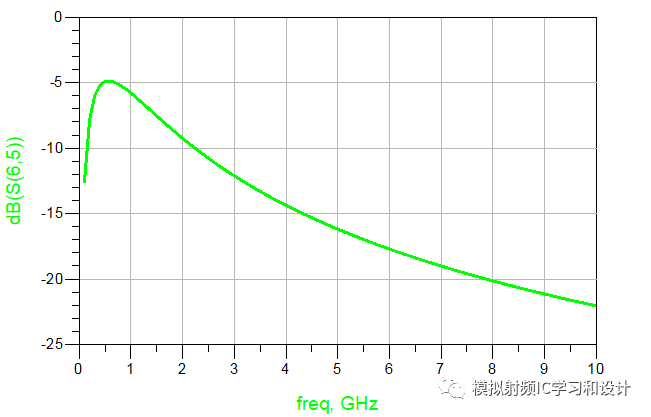
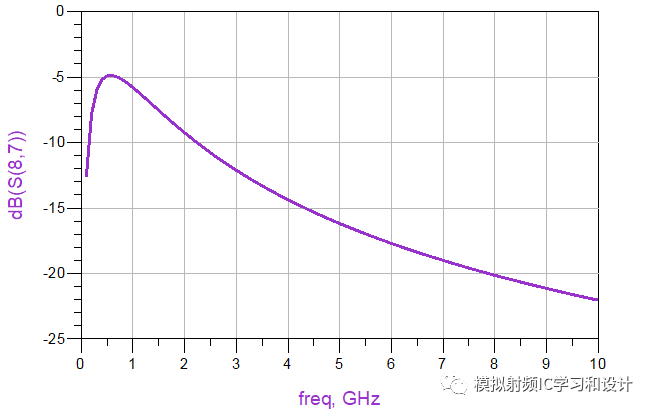
Amazing! 四个不同网络的S参数曲线完全相同，继续往下，上面是的无源网络只有电感，如果只有电容呢？如下图例子：

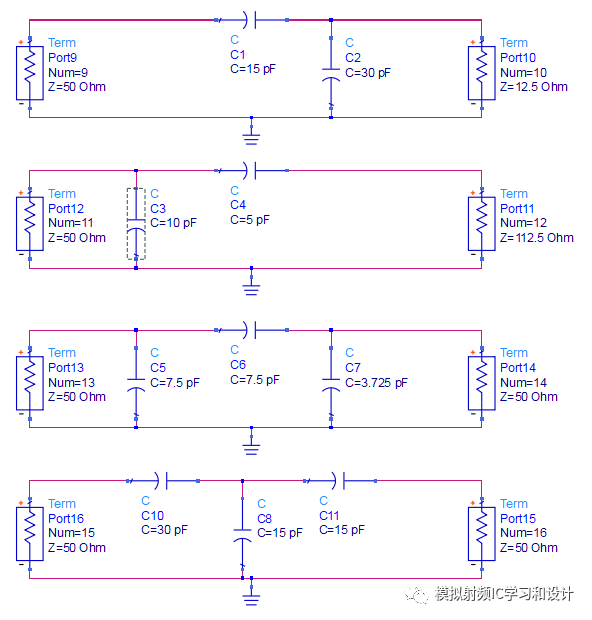
四个不同的电容网络，这四个网络的S参数怎么样，仿真图如下，正如你期待的，S参数完全相同。

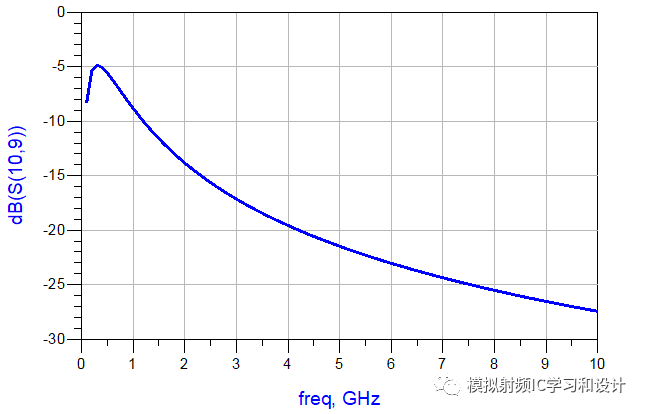
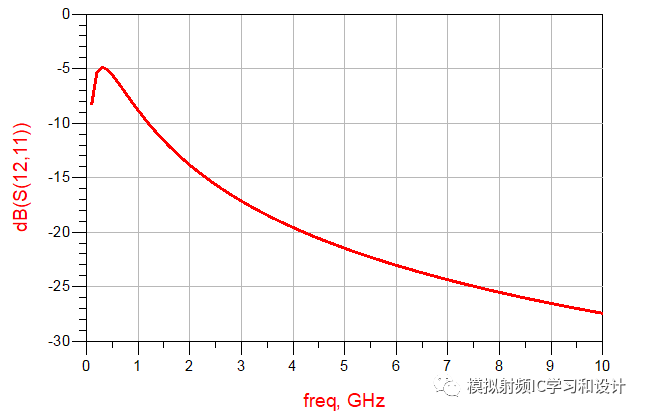
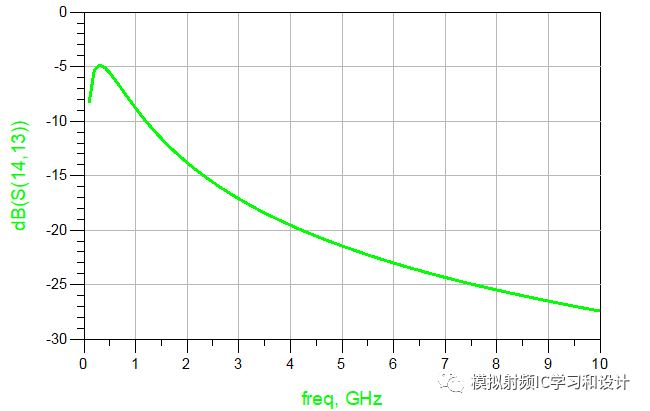
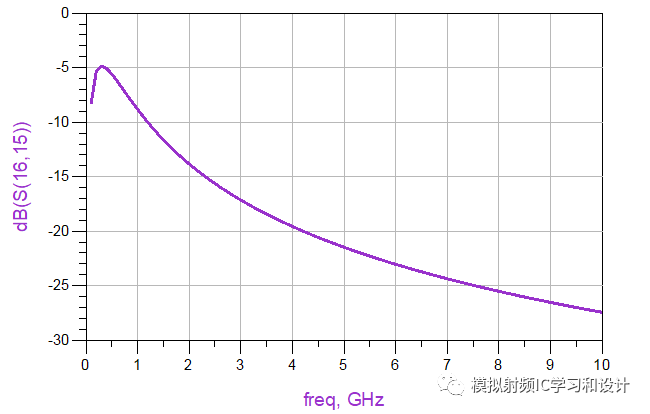
以上变换用到了今天所要说的Norton Transformation，Norton Transformation可用来改变网络的传输比，主要用于阻抗变换和滤波器的设计，仍然以上面的例子做说明，如下图所示，源阻抗50欧姆，终端阻抗12.5欧姆，这种二个L的结构称为左边型，可将其以一定的转换比转变成右边型的。

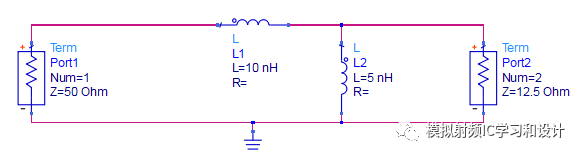
转变成右边型感值的终端阻抗都相应变大，转换比n=((10n+5n)/5n)^2=9，终端阻抗变为12.5*9=112.5，二个感值变大sqrt(n)=3倍。

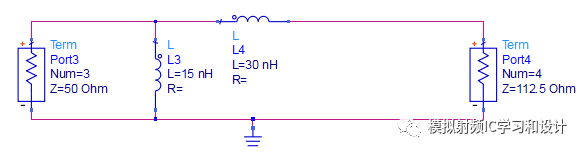
往往终端阻抗设计成50欧姆，意味着转换比只需要等于4就行，因此上面的结构并不适用，上面的结构用到了最大的转换比，实际上转换比可设计在1-max之间，这里设计转换比4，如下图所示，把5n拆成二个10n并联，对红框的二个L做Norton Transformation，此时的转换比n=((10n+10n)/10n)^2=4。

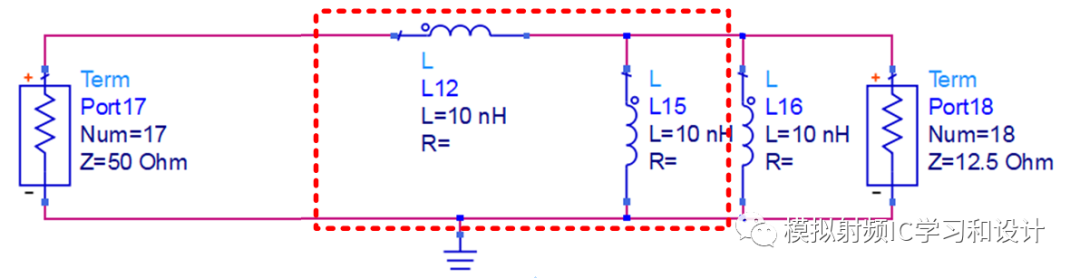
Norton Transformation后的电路如下，终端阻抗变大4倍到50欧姆，注意另外一个10nH（靠近终端阻抗）经过Norton Transformation后，也变大4倍到40nH。

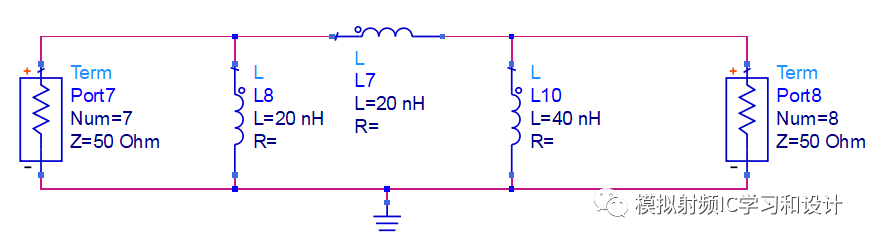
继续探索，实际把电路设计成转换比为4，除了上面的电路结构，还有另外一种电路结构，如下图所示，把串联的10nH电感分成二个5nH的串联，对红框的二个L做Norton Transformation，转换比n=((10n+10n)/10n)^2=4。

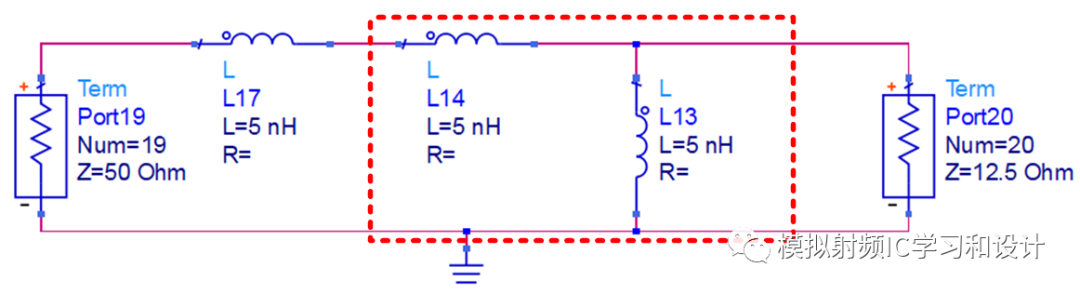
Norton Transformation后的电路如下，终端阻抗变大4倍到50欧姆，注意另外一个5nH（靠近源阻抗）经过Norton Transformation后，保持不变。

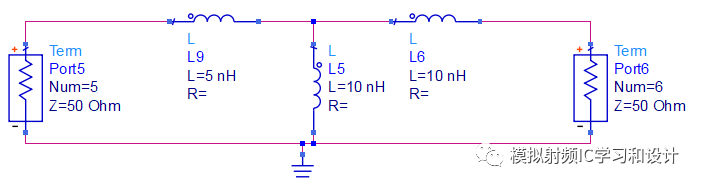
以上经过各种Norton Transformation后的网络传输特性完全相同，正如一开始的例子，其仿真的S参数完全相同，如果上面的二个电感变为二个电容，也可以同样做Norton Transformation，得到想要的转换比，和电感分析类似，需要注意电容和电感在形式上的差异。

上面阐述的是左边型转成右边型，终端阻抗向更高的值转换，如果一开始的网络是右边型的，其转换成左边型，那么可想而知，终端阻抗向更低的值转换，左边型到右边型和右边型到左边型，实际上是互易的，下面总结这四种结构：

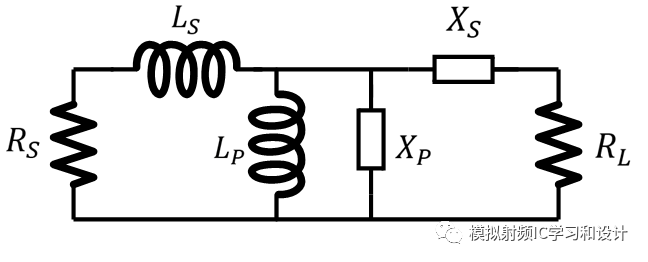
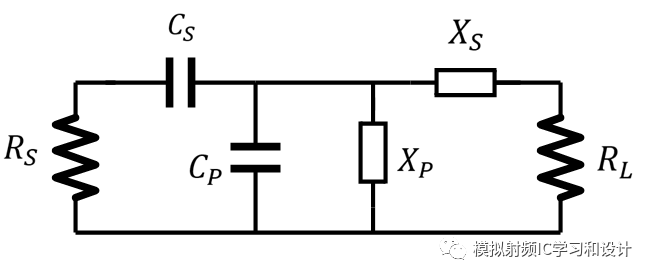
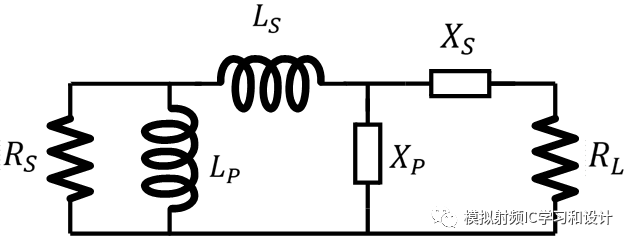
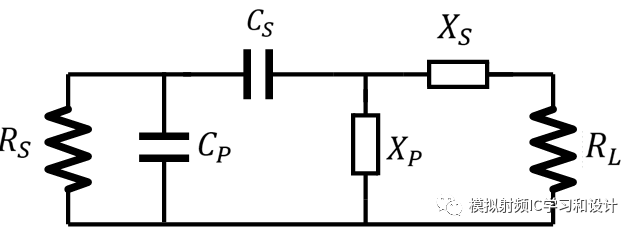
图中的终端阻抗不仅包含了电阻R，还包含了感性或容性元件，其经过Norton Transformation后，和终端阻抗具有同样的转换比，这里只给出第一种结构Norton Transformation后各元件的值大小，值已经标注在电路中（其它3种结构可以自行推导）

为了容易查看，从新贴上第一种结构：

最大转换比电路，其中转换比为：

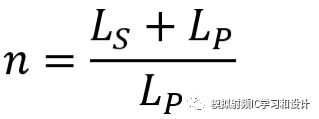
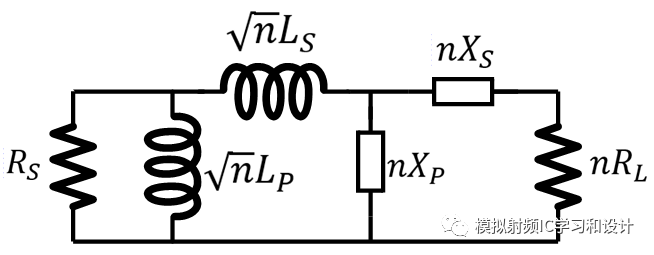
以小于最大转换比n的转换电路，转换比设为k，得到Pi型L电路：

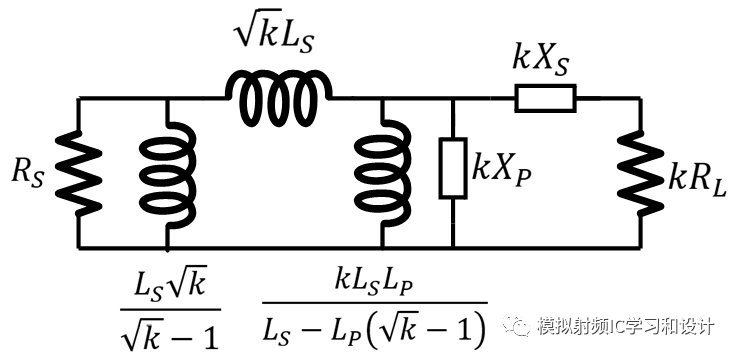
另一种转换比为k的电路，得到T型L电路：

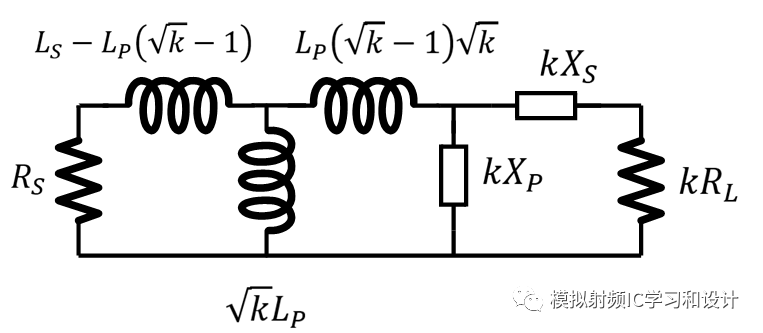
总结完毕！