加速度计和陀螺仪的工作原理

 

1. 概述

椭球拟合是一种用于校准加速度计传感器的方法。该方法假设各轴之间相互直，加速度传感器在静止状态（只受重力的情况下），在三维空间中，各个姿态的x,y,z轴的重力点都在一个球面上。然而，由于各轴之间都会有偏差，所以各姿态重力点都落在一个椭球面上。椭球的中心即为加速度的偏移量，也就是校准值。   椭球拟合的核心方法是最小二乘法。   最小二乘法，也称为最小平方法，用于通过最小化残差的平方和来找到一条最佳拟合直线或曲线，从而找到自变量和因变量之间的关系。目的是：用于找到一组参数，使得模型的预测值与观测值之间的平方误差最小化。换句话说，它找到了最能代表变量之间关系的直线或曲线。它可以应用于线性回归、多项式回归和其他类型的回归分析。 而线性回归是一种基于最小二乘法的统计方法，用于建立自变量和因变量之间的线性关系模型。

2. 加速度计的工作原理[1]

     在这里再简单的单独介绍一下加速度的工作原理，前面也写过一篇 《MEMS 惯性传感器 01-加速度计&陀螺仪工作原理》的博文详细介绍了加速度计和陀螺仪的工作原理。      我们依据姿态传感器的各轴的方向来想象有这样一个立方体的盒子，盒子里装有一个球。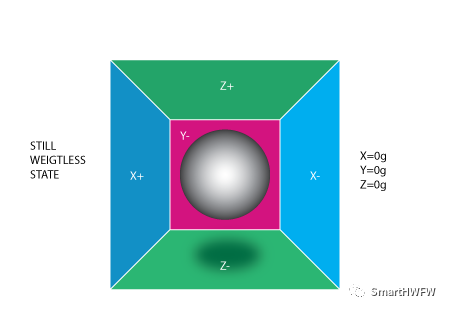

 01

假设我们把这个盒子放进太空（没有重力场），此时处于静止状态，三个轴的加速值都为[0, 0, 0]g。 如果我们突然将盒子向左移动（以加速度 1g = 9.8m/s^2 加速它），球将撞到 X-。然后，我们测量球施加到 X- 的压力，并在X轴上输出[-1, 0, 0]g 的值。 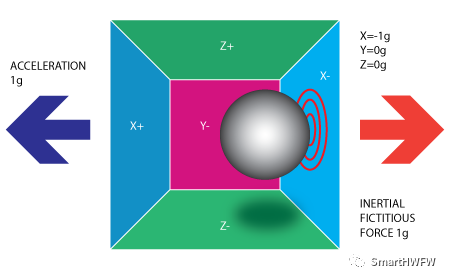         note：加速度计实际上将检测到与加速度矢量方向相反的力。  

02

现在我们把立方体的盒子放在存在重力的地球上，Z 轴向上放在地球上，盒体内的球受到地球重力的影响会落在 Z- 内壁上，并在内壁上施加 [0, 0, -1]g 的值。在这种情况下，盒子没有移动，但我们仍然在 Z 轴上得到 -1g 的读数。球施加在内壁上压力是由重力引起的。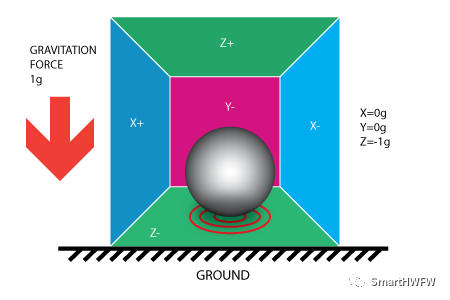             

04

我们将盒子倾斜 45° 时，球将接触 Z 和 X- 两个面墙，将重力加速度正交分解，测得的X、Z轴的值为都为  [-g/√2, 0, -g/√2]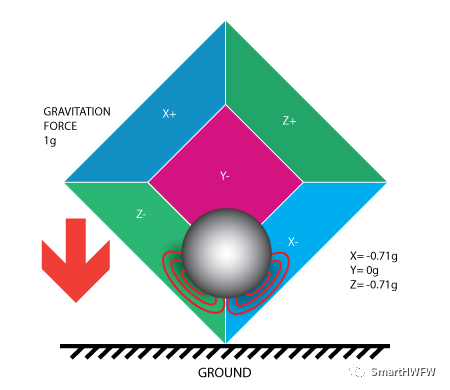               

3. 椭球拟合方法

 01

椭球拟合算法描述 椭球拟合，可对多个位置（N）进行测量，并可进行组合以找到未知数（偏移、增益和交叉轴增益）。   和正六面体校准相比，正立面体需要准确的翻转传感器设备6次。  但是，对于椭球拟合，不需要知道传感器的真实参考源，因为唯一的要求是真实参考源的模数是常数（X、Y 和 Z 的平方和的平方根）。   对于加速度计的情况：要仅测量重力，传感器不得有任何其他加速度；那么真实参考源的模数就是重力的模数   椭球拟合算法数学理论可以在网上找很多，我参考阅读的是：椭圆/球拟合法推导（快速入门）这篇[2]  https://blog.csdn.net/qq_39667840/article/details/106607279    

 02

椭球拟合流程    1）椭球面的标准方程为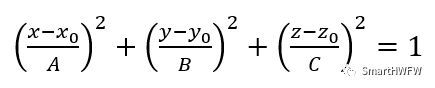：  需要拟合的参数有六个，他们分别是椭球的中心和半轴长    2）将标准方程写成一般形式为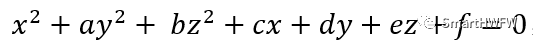： 通过对参数a、b、c、d、e、f的求解间接求出参数 x0 、y0 、z0 、A、B、C    3）建立误差方程  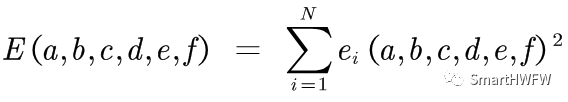  4）改写成目标函数  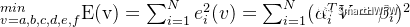 5）根据线性最小二乘理论，求最优解(即a,b,c,d,e,f) 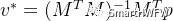其中 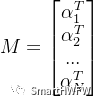 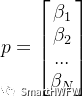     6）计算x0 、y0 、z0 、A、B、C  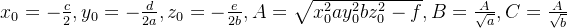 7）校准结果为：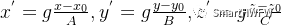

4. C语言实现椭球拟合

 01

源码    

 02

拟合计算出x0 、y0 、z0 、A、B、C 的值   ‍  

 01

拟合加速度计的前/后数据对比

4. 椭球拟合校准效果演示