测量中的数据采集系统-模数转化

2

数据采集系统中的模数转换(ADC)

模数转换的概念

模拟信号只有通过A/D转化为数字信号后才能用软件进行处理。模数转换，是将连续时间、连续幅值的模拟(Analog)信号转化为离散时间及离散幅值的数字(Digital)信号的过程(Analogue-to-Digital Conversion，常缩写成ADC)。

在实际测试过程中，我们关注的一些参数如声音，振动，温度，转速等都是时间的连续函数，这些参数电脑没有办法直接进行处理，只有经过模数转化变成离散的数字信号后，才可以进行保存，显示，处理，分析。因而，模数转化需要经过两个主要过程，即时间离散化，幅值离散化。

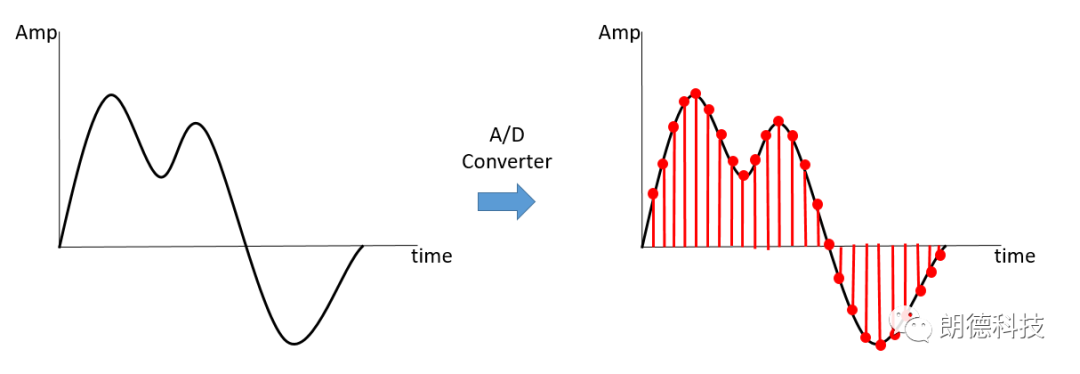
图1、模数转化示意

模数转换的技术要求

在测量和数字信号处理中，模数转换必须满足以下几个方面的技术要求：

（1）采样速率应满足采样定理(即Nyquist定律)，并适当加入抗混迭滤波器；

（2） 宽带化，通常对声学测量的模拟信号进行数字化，信号带宽通常在几到几十兆赫兹的范围，而可听声通常要测量到几十千赫兹；

（3）足够高的信号动态范围；

（4）减少量化噪声。

时间离散化（采样）

时间和幅值上都连续的模拟信号，在经过采样后，会转变为时间上离散的模拟信号。

一个频带限制在（0，fH）内的连续信号x(t)，如果抽样频率fs大于或等于2fH，则可以由抽样序列{x(nTs)}无失真地重建恢复原始信号x(t)。

由低通采样定理可知，若抽样频率fs<2fH，则会产生失真，这种失真称为混叠失真。

以下图的正弦曲线为例，我们只需要一些特殊的点，如相邻的两个零点的位置（红色点），或者相邻的波峰和波谷位置（绿色点），再按照正弦的规则，我们就可以还原出正弦曲线。

图2、正弦信号时间离散化采样

同样还是以上图为例，正弦信号的周期为1，而我们的采样点，无论是红色点还是蓝色点，其采样间隔均为0.5，为正弦信号的一半，因此采样周期必须为信号周期的2倍。

尽管我们测试中碰到的所有信号都是复杂信号，但通过傅里叶变化，任何复杂信号都可以转为若干个正弦信号的和，再根据Nyquist定律，找到信号中最大的频率成分，使用2倍最大频率成分的采样率，从理论上，就可以通过离散信号重建出连续信号了。

以远大于低通采样率进行采样的方法称为过采样技术。采用过采样技术会带来以下两个好处：

（1）高速采样可降低对前级抗混叠滤波器性能的设计要求。采样率越高，则采样后频域中相邻的两个周期性频谱之间的间隔越大。因此即使前级滤波器在截止频率附近的阻带衰减不足，所产生的混叠效应也会减轻，相应的恢复后信号的失真也会减小。

（2）高速采样可提高信噪比。由于存在着量化噪声，ADC的信噪比近似表示为：

其中，N为ADC的分辨率，fs为采样速率，fmax为输入模拟信号的最大频率。由上式可见，采样率fs每提高一倍，信噪比增加3dB。

以目前很火的新能源电机PWM噪声为例，其频率已超过20000Hz，若还是以常规的44100Hz的采样率，其结果显示会有缺失，借助Mecalc公司的ICP42采集卡，其采样率可达到102.4KHz,而ICP42S，其采样率达到204.8KHz，足以满足新能源PWM噪声测试要求。

图3、新能源电机PWM噪声

对于ADC而言，采样速率和分辨率是两个非常重要的指标参数。其中，采样速率表示模拟信号转换为数字信号的速率，与ADC器件的制造技术有关，取决于ADC中比较器所能提供的判断能力。分辨率表示模拟信号转换为数字信号后的比特数。

幅值离散化（位数精度）

位数精度(Bit Resolution)表示在允许的模拟信号输入范围内可以产生的离散值的数量，也可以理解为需要引起离散值变化，输入信号电压所需要变化的最小幅值。

假设输入电压的范围为（-V,V），位数精度为N，则经过模数转化后幅值精度为：

由此可以看出，电压输入范围越小，位数精度越高，则经过模数转化后幅值精度越高。

同样，还是以正弦信号为例（如图4），其幅值为0.8，时间离散化（采样）不变，均为10Hz，在进行 幅值离散化（位数精度） 的过程中，不同的数位精度，采样点对应的幅值也不同。

假设选择一个12位ADC，则它可在输出端以4096个数字表示施加于转换器输入端的任何信号。这些表示信息确实存在有限量的误差。因此，如果12位ADC的输入满量程(VFS)为10 V p-p，那么其理想情况下的LSB大小为2.44 mV p-p，精度为±1.22 mV。

图4、正弦信号幅值离散化

对于数据采集系统中重要模数转化环节而言，如果拥有较高的采样率以及位数精度，那么测试结果的准确性也就更高。ADC的信噪比（SNR）反映了量化过程中产生的无噪声信号部分的均方根值和量化噪声的均方根值的比值。若输入信号为归一化的正弦波1/2sin(ωt+ψ)，则可以通过式(1)确定SNR的大小。由此可知，ADC的信噪比主要取决于分辨率，分辨率每增加一位，ADC的信噪比将增加6dB。但是随着分辨率的提高，ADC的量化电平变得更小，采样过程更容易被干扰。

对于实际的A/D变换系统，由于存在着电噪声、外界干扰和模拟电路的非线性畸变等因素的影响，仅以理想的分辨率来度量系统性能是不够的。为更好地反映系统性能，可以在测量得到SNR的基础上，将上述因素按量化噪声进行折算，推导出系统的有效转换位数（ENOB）。其计算公式如下：

ENOB表示了理想的ADC器件为达到实际的SNR所需要具有的分辨率的大小。ADC器件指标中ENOB与分辨率的差别，反映了由于误差源引起的SNR下降所造成的采样精度下降的程度。

图5、理想ADC的量化误差

图6、实际ADC量化过程中产生的误差

图7、实际ADC量化过程中的主要误差来源

下图中列举了Mecalc公司使用频率最高的采集卡模块的采样率及位数精度详细参数，从图中可以看到， 102.4k/s的采样率已经基本覆盖，部分采集卡可以达到1M/s，同时，所有采集卡位数精度均为24bit。

图8、Mecalc公司采集卡参数列表