详解从均值滤波到非局部均值滤波算法的原理及实现方式

图像降噪处理主要分为2D（空域）与3D降噪（时域/多帧），而2D降噪由于相关的实现算法丰富，效果各异，初学入门有着丰富的研究价值。理解2D降噪算法的流程，也对其他的增强算法有很大的帮助，因此本文将再啰嗦一次，详解从均值滤波到非局部均值滤波算法的原理及实现方式。

细数主要的2D降噪算法，如下图所示，从最基本的均值滤波到相对最好的BM3D降噪，本文将尽量用最同属的语言，详解这些算法的实现流程，并给予一定的FPGA加速实现的实现思路。其中BM3D由于篇幅较大，后面再补上。

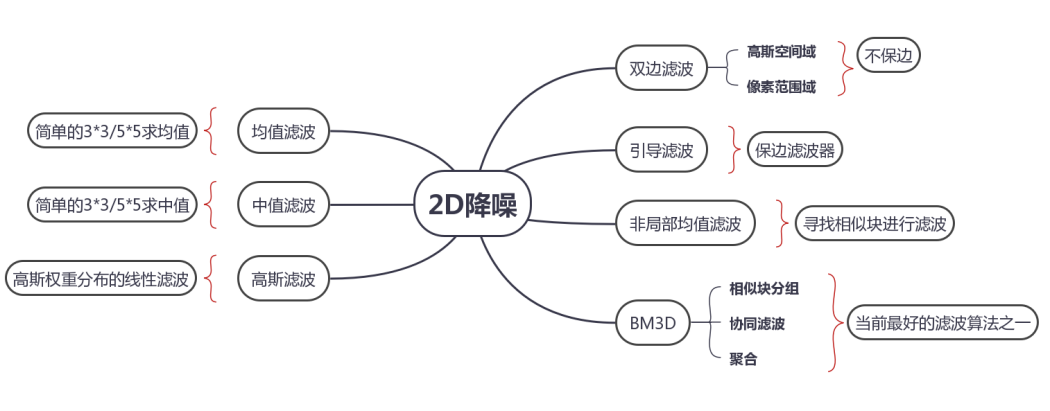
1.1. 均值/中值滤波

首先所有滤波算法都是通过当前像素周边的像素，以一定的权重来计算滤波的像素值。因此主要涉及两个变量：窗口的大小，以及窗口内像素的权重。以最简单的均值滤波/中值滤波，3*3窗口为例，计算及优缺点如下：

对于FPGA的硬件加速实现，过程还好，唯一头疼的就是涉及了除法，由于除法计算时钟周期长且耗费LE，我们需要升级改造下，因此优化公式如下（sum为9个像素累加的结果），将除法巧妙变成乘法：

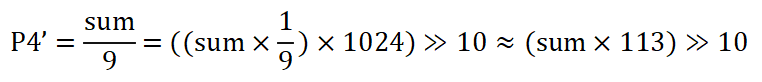
因此实现的流程如下

1）sum1=P0+P1+P2; sum1=P3+P4+P5; sum3=P6+P7+P8，即先求每行3像素累加

2）sum=sum1+sum2+sum3，即求三行9像素累加

3）sum*144，取结果的[17:10]，即为均值滤波的结果。

4）以上过程流水线，最终每个clk输出一个计算结果。

备注：这里1024/9取了floor，这样保证不会溢出。

对于中值滤波而言，本身计算并不复杂，就看怎么取巧最快得到中间数，网上流传了一个三步法，即如下图所示，

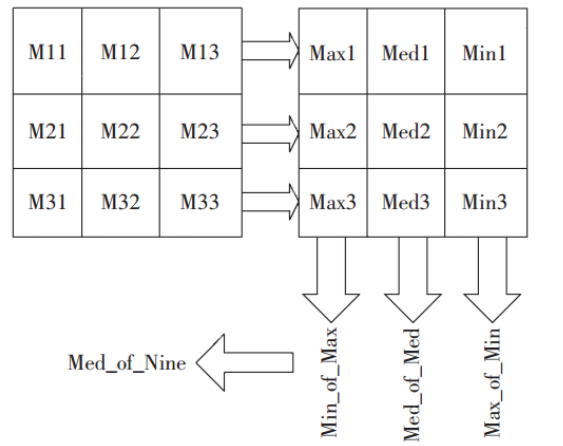
那么FPGA硬件加速实现，流程如下：

1）计算每行3个像素的最大中、中值、最小值

2）计算三个最大值的最小值，中间值的中间值，以及最小值的最大值。

3）对上述三个值求得中间值。

4）以上过程流水线，最终每个clk输出一个计算结果。

中值滤波计算相对均值滤波稍微复杂一点，但是好处是只用了比较器，没用乘法器，比均值滤波更省资源。

对于椒盐图像的均值滤波、中值滤波计算效果对比，如下所示，分别为椒盐图像、均值滤波、中值滤波结果。

1.2. 高斯滤波

1）

前面讲的均值/中值滤波，对于窗口内每个像素的权重都是一样的，噪声在图像当中常表现为一引起较强视觉效果的孤立像素点或像素块，那么他必然不是平均分布。

正态分布是最重要的一种概率分布，相关概念上是由德国的数学家和天文学家Moivre与1733年首次提出的，但由于德国数学家Gauss率先将其用于天文学研究，因此也叫做 高斯分布 。在正态分布里，人为中间状态是常态，过高和过低都属于少数，因此正态分布具有相当的普遍性，典型的比如升高、寿命、血压、成绩、测量误差等都遵从正太分布。

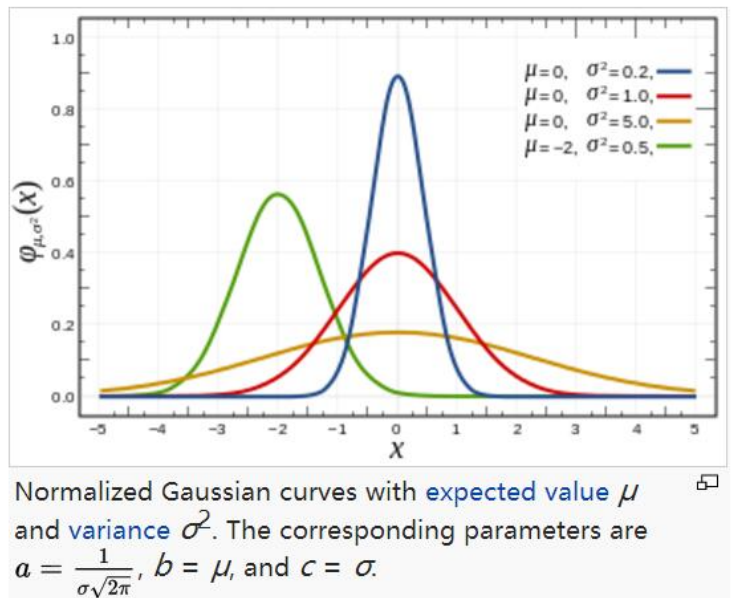
因此以概率论及中心极限定理（https://wiki.mbalib.com/wiki/中心极限定律）猜想，大部分噪声应该也符合正态分布/高斯分布（ 高斯白噪声 ），所以也就有了高斯滤波，及根据正态分布进行权重计算的滤波方法。上图曲线是高斯分布的一维函数，而图像应该是二维的，图解如下二维高斯分布：

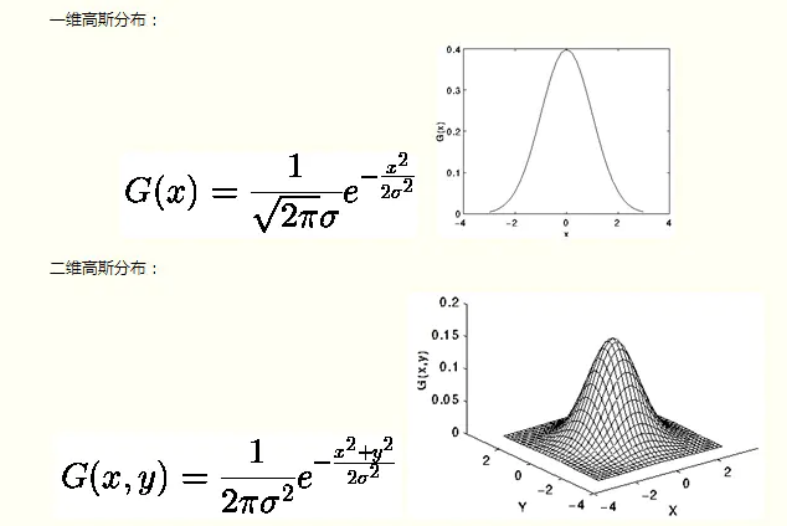
既然已经得到二维高斯分布函数，那么根据窗口到目标像素的距离，就可以是计算出周边像素的权重——高斯模板。均值滤波每个像素的权重都是1/9，再通过卷积后计算得到结构，而高斯滤波就是根据正态分布，去计算当前像素相对距离的权重值，假定σ=1.5（σ就是滤波的强度），3*3的高斯模板计算计算过程如下：

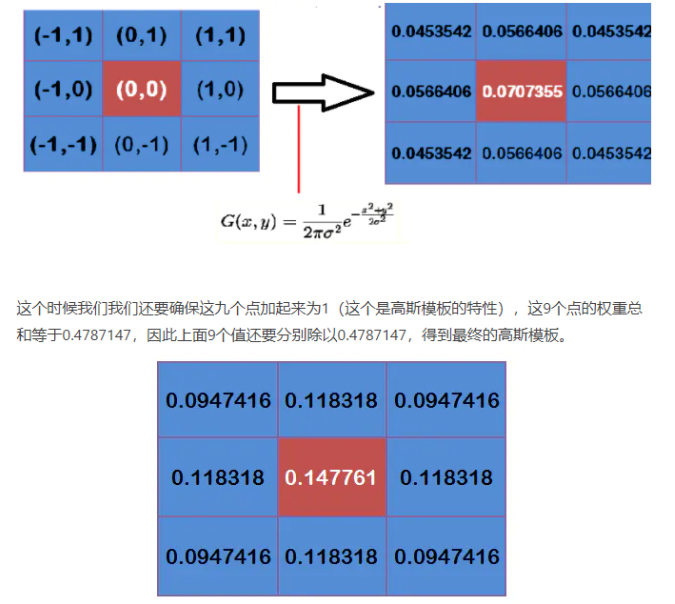
但是这还不够，毕竟我们的目标是直接上FPGA，那必须顶定点化，因此假设扩大1024倍，则3*3的高斯模板定点化如下：

对于33或者55，选定的σ，高斯模板那么，现在计算就简单了，卷积后再缩小1024倍即可，采用FPGA计算，过程如下：

1）计算9个像素的对应卷积参数的乘法

2）9累加9个乘法结果

3）右移10bit或取结果的[17:10]，即为高斯滤波的结果。

4）以上过程流水线，最终每个clk输出一个计算结果。

备注：当然实现还可优化，比如只用3个乘法器，算一行累加一行，也就4个时钟算完。

最后，暂且盗用别人针对不同σ的3*3高斯滤波效果图，如下（σ越大越模糊）：