

分享一种模拟滤波器设计方法
电子说
描述
不知道大家有没有这样的疑问:我明明是在学“数字滤波器设计”,怎么突然冒出一个“模拟滤波器设计”来?我是不是学了个假的数字信号处理?
我们首先来解释一下。
第一,大多数数字信号处理系统中不可避免地要用到模拟滤波器,比如:AD转换器前的抗混叠滤波器、DA转换器之后的平滑滤波器,都是模拟滤波器。因此,模拟滤波器设计也是数字信号处理中应当掌握的技术。
第二,我们说了,IIR滤波器设计的一种重要方法称为“ 模拟原型法 ”,就是 首先设计模拟滤波器,然后转换为数字滤波器 。这种方法有历史原因的,在历史发展的长河中,模拟滤波器先出现,几十年之后才出现数字滤波器。在数字滤波器出现之前,模拟滤波器已经形成了一套完善的设计方法。所以人们自然而然地想法就是,先设计模拟滤波器,再转换为数字滤波器。
这两点,是我们把“模拟滤波器设计”的内容放在本章中学习的原因。
在正式内容开始之前,为了更好地理解,我们首先做几点铺垫:
第一点,本节中,因为讨论对象是模拟系统,所以所涉及到的角频率变量都是大写的Omiga(文字中只能用W表示),即“模拟角频率”。系统函数和频率响应函数用Ha(s)/Ha(jW)表示(“a”为analog的第一个字母);
第二点,在本章中,我们一般只关注其幅频特性|Ha(jW)|,因为模拟滤波器的相频特性一般都是非线性的。
第三点,IIR滤波器的设计方法,是用一些形状合适的数学函数,通过调节函数中的某些参数,来直接逼近滤波器的幅度函数,使其满足性能指标的要求。其目标依然是 确定系统函数Ha(s)分子分母多项式的阶数以及系数 。
第四点,上面所说的“形状合适的数学函数”,一般是作为滤波器的 幅度平方函数 ——也就是幅度函数的平方,即|Ha(jW)|^2。有的同学可能会有疑问“为什么不直接作为幅度函数,而是幅度平方函数”,这个疑问放一放,等到下面第二个问题就明了了。
一 幅度平方函数
幅度平方函数,顾名思义,就是幅度函数的平方,也就是:|H(jW)|^2。
在这里我们要解决一个问题:已知|Ha(jW)|^2的函数表达式,如何求Ha(s)?
有的同学说了,这个简单,把|Ha(jW)|^2开平方,得到Ha(jW),然后令jW=s,就得到Ha(s)了?
你有这样的想法,说明你 too young too simple。首先,|Ha(jW)|^2开平方,只能得到 |Ha(jW)| 而非 Ha(jW),因为|Ha(jW)|^2不包含相位信息,也就是说,如果没有其他限定条件,|Ha(jW)|^2不能得到唯一的Ha(s)。

那是不是说,我们开平方后得到|Ha(jW)|,然后给它配上一个我们需要的相频函数,构造出 Ha(jW)=|Ha(jW)|e^j[fai(W)],再令 jw=s 得到 Ha(s) 就可以了呢?
这个想法,理论上说好像可以。但是实际中我们不是这样处理的。因为我们研究的都是实系统,即ha(t)为实函数、Ha(s)为有理函数(通过多项式的加减乘除得到的函数,其系数是实数),显然,用上面所说的方法是无法得到有理函数形式的 Ha(s) 的。
那应该怎么办呢?我们首先从公式上推导一下 |Ha(jW)|^2 与 Ha(s) 的关系,如下式:
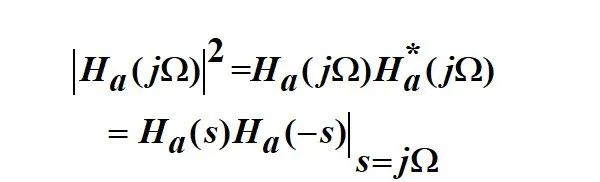
上述结论的推导过程如下:
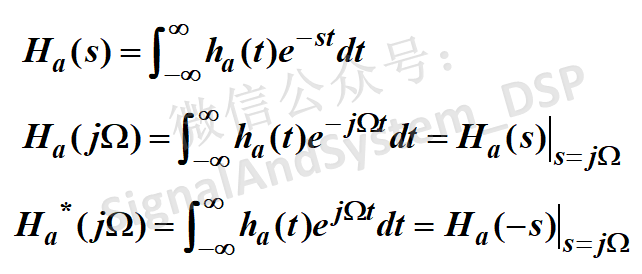
这个关系说明什么呢?
如果s0是Ha(s)的极点,那么 -s0 一定是Ha(-s) 的极点,而且,s0 和 -s0 二者都是 Ha(s)Ha(-s) 的极点。零点亦是如此。
也就是说,实系统的 幅度平方函数的极点必然共轭成对、并且以虚轴镜像成对出现。零点也是这样。 更通俗地说,就是:如果在实轴上,就是两个一对,下图中的(P5,P6);如果在虚轴上,貌似两个一对,实则四个一对,因为是二阶极(零)点,如下图中的(A5,A6);如果既不在实轴也不在虚轴上,就是四个一对,如下图中的(A1,A2,A3,A4)和(P1,P2,P3,P4)。
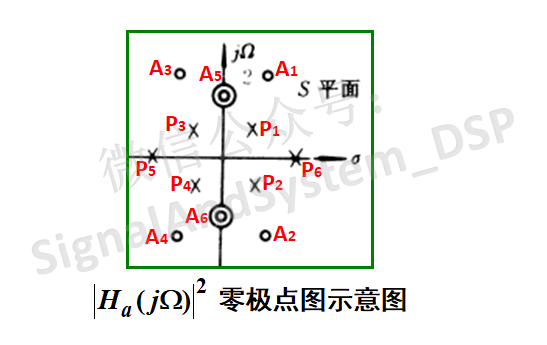
到这里,下面的问题就好办了。我们选一半极点、一半零点给Ha(s),剩下的一半给 Ha(-s),就可以了。极点零点一旦确定,Ha(s) 有理分式的形式就可以写出来了。
显然,选哪些分给Ha(s)、哪些分给Ha(-s),有多种选择方法。但是也要满足一定的约束条件。
首先,要保证是实系统,极点和零点都必须共轭成对;第二,为了保证系统为因果稳定系统,极点只能选择左半平面的分给Ha(s)、右半平面的分给Ha(-s),零点不影响稳定性,故不受此约束;第三,可以根据相位特性的要求,选择一半共轭成对的零点分给Ha(s)、另外一半分给Ha(-s),例如,如果要求是最小相位系统,零点也必须位于左半平面。
解决了“由幅度平方函数得到系统函数”的问题之后,下面,我们就来看哪些数学函数适合做滤波器的幅度平方函数。我们以低通滤波器为例。
两位大咖即将隆重登场,分别是巴特沃斯和切比雪夫。
二 巴特沃斯滤波器
1. 巴特沃斯函数
巴特沃斯是谁?英国一名普普通通的工程师,全名斯替芬·巴特沃斯(Stephen Butterworth),凭借1930年发表在英国《无线电工程》期刊的一篇论文而名垂青史。
巴特沃斯函数的表达式为:
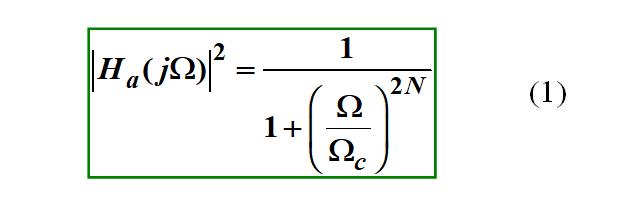
在这个表达式中,W为变量,N和Wc为常数。这个函数很简单,但是设计的很巧妙。
我们先来认识它一下,看一看它的模样。
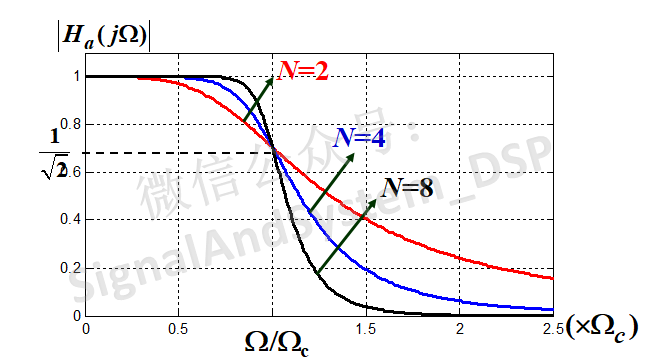
上图是以W/Wc为横轴、|Ha(jW)| 为纵轴画的图(用matlab画的),分别画出了N=2、N=4和N=8时的图形。
然后,我们来分析一下它的特点:
特点一:W越大,函数值越小。而且,它的前 2N-1阶导数在W=0处都为零,表明在 W=0 附近一段范围内都是非常平直的。故“最平响应特性滤波器”的称号它当之无愧;
特点二:N越大,通带增益越平坦,频带边缘下降越陡峭,即越接近理想性能。从上图中也可以看出来,黑、蓝、红这三条线,显然是黑色(N=8)时代表的滤波器性能最好;
特点三:三条线都交于一点(W=Wc)。这是显然的,当W=Wc时,|Ha(jW)|^2=1/2,与N无关,转换为dB就是10log(1/2)≈-3dB,所以称 Wc 为 **3dB带宽** 。这一特点,称为“3dB带宽不变性”(即与N无关);
特点四:此函数,没有零点,故称为全极点型滤波器。
2. 巴特沃斯函数的极点
下面,我们来求一下巴特沃斯函数的极点。
令公式中的 jW=s,得到:
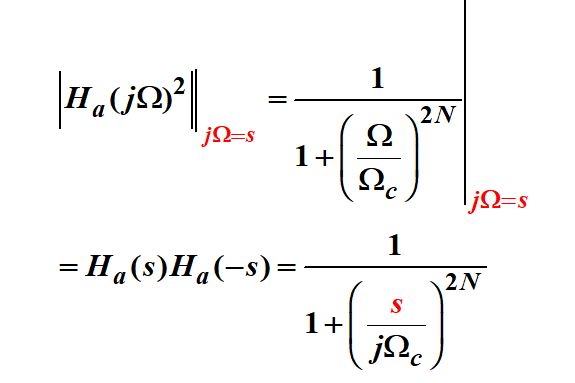
求极点,也就是令分母多项式为零,得到:
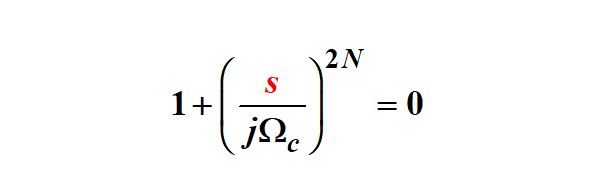
解上面的2N阶方程,得到2N个根(极点):
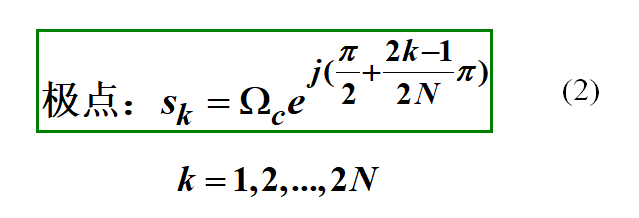
用公式表示,看上去似乎很复杂,我们以N=3为例,这6个极点分别为:
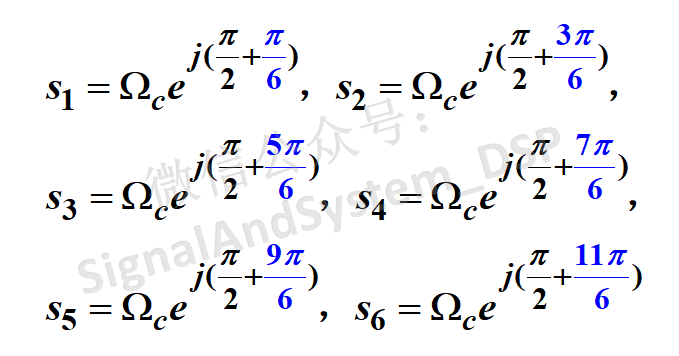
画在图上(零极点图)就一目了然了:
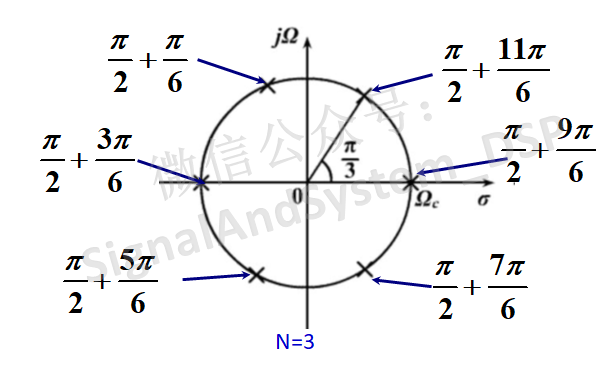
也就是说,Ha(s)Ha(-s)的 2N 个极点等间隔地分布在半径为 Wc的圆上。
说到这里,我们开篇时的那个疑问 “ 为什么不直接作为幅度函数,而是幅度平方函数 ” ,也找到答案了。不能把它直接作为幅度函数,否则无法得到因果稳定系统。而作为幅度平方函数,我们只要取左半平面的N个极点构成Ha(s),就可以由幅度平方函数得到系统函数了。并且,根据极点,构造出的系统函数Ha(s),自然就是有理分式的形式。
看到这里,有的小伙伴会担心地想 “ 如果极点在虚轴上,那可咋办呢?”。其实,我们观察一下极点sk的表达式就是发现,这个担心是多余的,巴特沃斯函数的极点永远不会落在虚轴上。
总结一下,N阶巴特沃斯函数构成的滤波器的系统函数是:
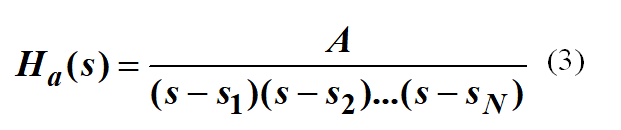
常数A怎么确定呢?
简单,我们只要取一个特殊点(最简单的当然是W=0,或者说s=0),分别代入到(1)式和(3)式中,就可以得到:
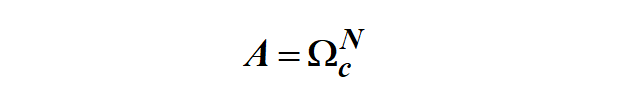
即:N阶巴特沃斯函数构成的滤波器的系统函数是:
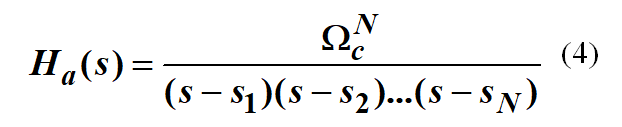
3. 巴特沃斯滤波器的阶数
所谓的滤波器设计,就是得到系统函数,也就是上面的(4)式。可见,只要求出N和Wc,就万事大吉了。
N和Wc怎么确定呢?当然是根据滤波器的性能指标来确定。
下面首先来看,阶数N怎么求。
我们知道,N越大,通带性能越平坦(即通带衰减越小),而阻带衰减越大,并且过渡带越窄,即滤波器性能越好。这只是一个定性的分析,要定量的分析,还要从公式出发。
首先,我们来看一看滤波器的性能指标,看下图:Wp、Ws分别为通带截止频率和阻带截止频率,Ap、As分别为通带最大衰减和阻带最小衰减(均以dB为单位)。而巴特沃斯函数是单调递减的,所以,只要当W=Wp时,衰减不大于(即≤)Ap、W=Ws时,衰减不小于(即≥)As,那么在通带内和阻带内,肯定是满足技术指标要求的。
注意 分清这三个W ,Wc是3dB截止频率,即W=Wc时,幅度特性正好是-3dB,而一般来说,通带最大衰减Ap要小于3dB,而阻带最小衰减As一般为几十dB以上,所以,一般来说,Wc要大于Wp而且远远小于Ws。
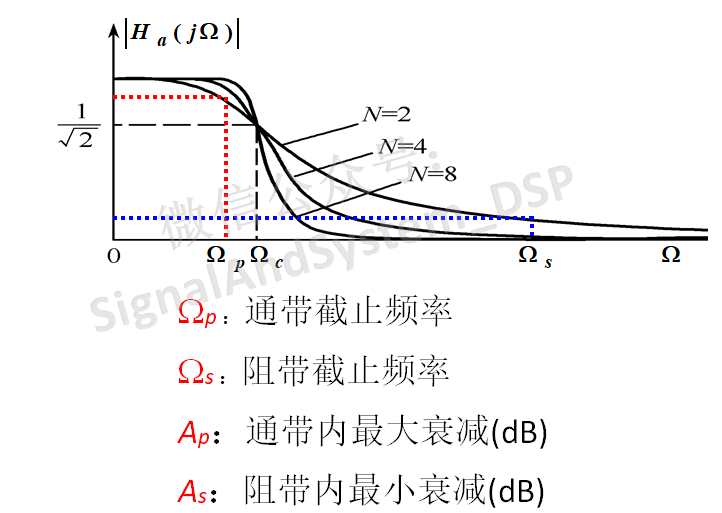
这样,我们只要把 W=Wp 和 W=Ws 代入到巴特沃斯函数中,然后取10倍的log(转换为dB),得到两个不等式:
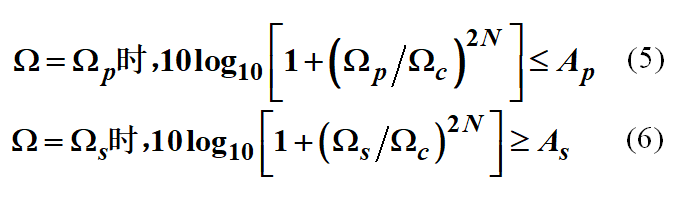
根据(5)和(6)可得:
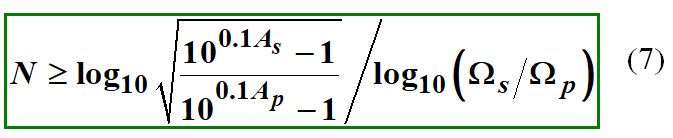
这样,将表示技术指标的这四个值带入上式中,就可以得到满足该指标的滤波器阶数N的条件,取满足该条件的最小的整数(例如得到4.21,我们就得取N=5),就是我们需要的滤波器阶数。
4. 巴特沃斯滤波器的3dB截止频率
N确定了,巴特沃斯函数中还有一个参数:Wc 怎么得到呢?
将刚刚求出的N带入到上图的(5)式或者(6)式中(把≤和≥变为=),都可以得到 Wc。显然,这两个Wc是不同的。
如果用(5)式取 = 号得到的Wc,即
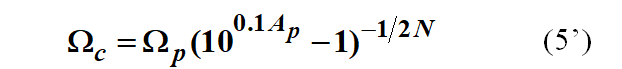
那么,通带最大衰减刚刚好满足指标要求,而阻带最小衰减会略大于指标要求。这是因为,我们按照(7)式得到的往往不是整数,我们实际上取的N是大于临界条件的最小整数。
阻带衰减越大,说明滤除得更彻底,也就是说,如果根据(5)求出的Wc,我们的巴特沃斯滤波器的通带性能刚刚好满足指标要求,而阻带性能会略高于要求(也可以称之为有富裕)。
反之,如果用(6)式取 = 号得到的Wc,即
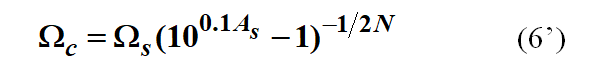
那么,阻带最小衰减刚刚好满足指标要求,而通带最大衰减会略小指标要求。此时,通带性能有富裕。
如果设计任务本身就是设计模拟滤波器,那么就可以根据实际需要,来决定用(5)式或者(6)式来确定Wc。如果没有特殊要求,用哪个都行,都能得到满足性能要求的滤波器。
正如我们前面所说,在实际使用中,“模拟滤波器”设计一般是数字滤波器设计的中间一步,可以根据模拟滤波器转换为数字滤波器时采用的方法对滤波器幅频特性的不同影响,来选择那个式子求Wc。这一点,在下一篇中还会涉及到。
5. 巴特沃斯滤波器的设计
总结一下,根据前面所述,巴特沃斯滤波器设计可以按照下面的步骤:
第一步,根据滤波器性能指标,确定N和Wc;
第二步,根据N和Wc,求出幅度平方函数的2N个极点;
第三步,取左半平面的N个极点,构造出滤波器的系统函数Ha(s)。
上述步骤,从原理上讲,是没问题的。但实际上,还有更简便的方法。我们的前辈工程师们是很聪明的,他们想到了,将Wc设为1(称为 归一化 ),针对N=2、3、4......,分别计算出对应的滤波器(称为归一化原型滤波器)的系统函数HaN(s)的系数,存成表格。
这样,在具体应用场景中,只要计算出阶数N,去查表,然后做一个神奇的操作—— 去归一化 ,就可以得到所需要的滤波器的系统函数了。
这个神奇的操作——去归一化,到底是怎么回事呢?看下图:

下面解释一下上图的这个去归一化是怎么回事。
我们把(4)式的分子分母同除以Wc,然后,令s/Wc等于 p (称为归一化复变量),得到一个新的函数,我们记为HaN(p),我们称之为归一化原型滤波器的系统函数,它的极点pk,称为归一化极点。
相反的过程,也就是根据HaN(p),令 p=s/Wc,重新得到关于s的函数Ha(s),称 为去归一化 。
把(8)式的分母展开,就得到:
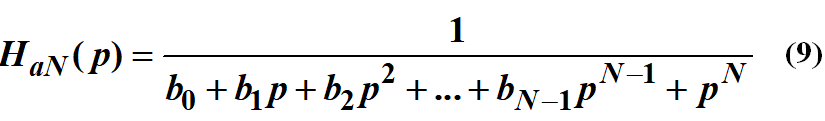
注意,常数项b0一定等于1,而且最高次项p^N的系数也一定是1。
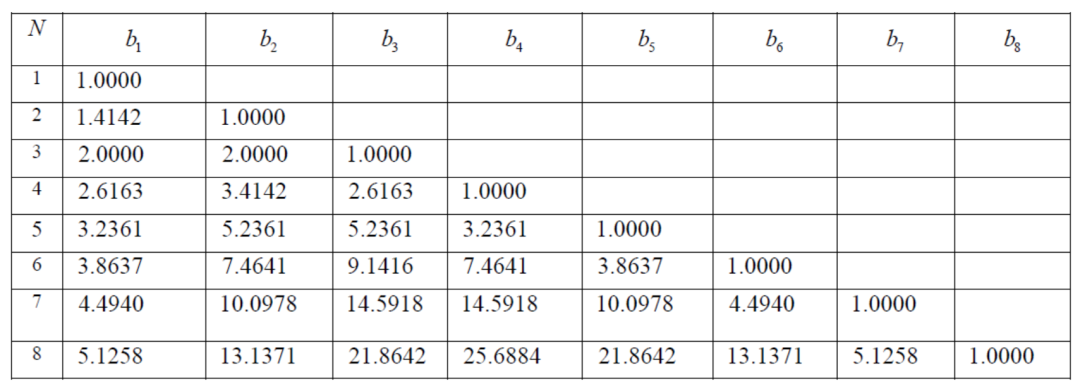
上式中的系数bi,前辈工程师们在上个世纪三十年代没有计算机的帮助下用铅笔和稿纸手工千辛万苦计算而形成了表格。只要计算出了阶数N,直接查表就可以了。
利用归一化的思想,修正一下前面总结的设计步骤,如下:
第一步 ,根据滤波器性能指标,确定N;
第二步 ,根据N,查表得到归一化滤波器的系数;
第三步 ,求出Wc,去归一化,得到Ha(s)的系数。
讲了这么多,还是要拿道题目来练练手吧。

【解】:
第一步,求N。
根据滤波器指标
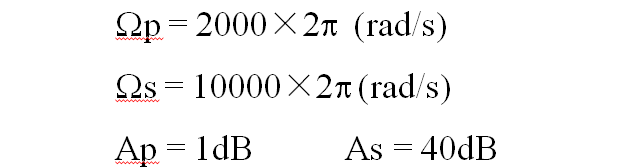
带入(3)式得到:N≥3.28
所以,取N=4
第二步,查表,得到归一化原型滤波器系统函数 HaN(p) 的系数b1、b2、b3如下所示;
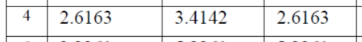
所以,归一化原型滤波器的系统函数为
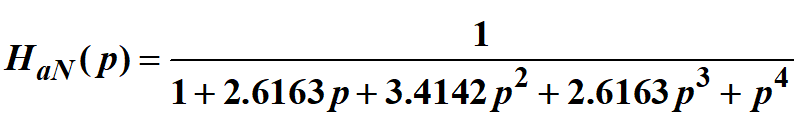
第三步,求Wc。
如果用(5‘)式求Wc,得到:
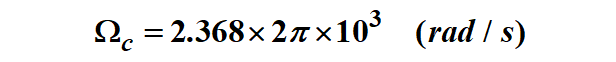
如果用(6‘)式求Wc,得到:
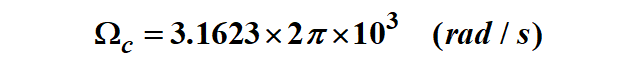
第四步,去归一化
得到巴特沃斯滤波器的系统函数为

6. 巴特沃斯滤波器的特点
巴特沃斯函数函数的特点,决定了巴特沃斯滤波器的特点,也就是幅频特性曲线是W的单调递减函数,这样的特点,是好?还是不好呢?
比如前面那道例题,我们设计得到的4阶巴特沃斯滤波器,在2kHz处衰减为1dB,那么在频率小于2kHz处,衰减会小于1dB。同样的,在频率大于10kHz处,衰减会大于40dB,当然这没有问题,因为毕竟通带内衰减越小越好,而阻带内衰减越大越好。
但是,从实现的角度来看,这一特点并不 “划算”,或者说,不经济,比较费钱。因为阶数越高,对系统硬件性能要求越高,成本越高。我们宁愿,通带和阻带内的特性均匀分布。也就是说,更经济的方法是,不是采用单调递减特性的巴特沃斯函数,而是采用其他具有某种起伏特性的函数,只要能够控制其起伏的范围就可以。
这就是下面要说的切比雪夫滤波器和椭圆滤波器。
三 切比雪夫滤波器
相比于名不见经传的巴特沃斯,切比雪夫可以说是大名鼎鼎,他是一位著名的俄国数学家。我们用到的,就是以他的名字命名的一种多项式——切比雪夫多项式:
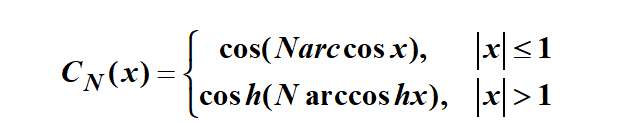
这个多项式的特点是:当 |x|≤1时,CN(x)是余弦函数,具有等波纹幅度特性;当|x|>1时,是双曲余弦函数,随x单调增加。
下图中这些五颜六色的线条,分别是N=0(蓝)、N=1(绿)、N=2(红)、N=3(黑)、N=4(黑)、N=5(紫)时的切比雪夫多项式CN(x) 曲线。可见,在 |x| < 1 范围内,都具有等波纹,N的数目决定了波动的次数;在 |x| > 1范围内,具有单调递增或递减的特点,并且N越大,递增或递减的速度越快。
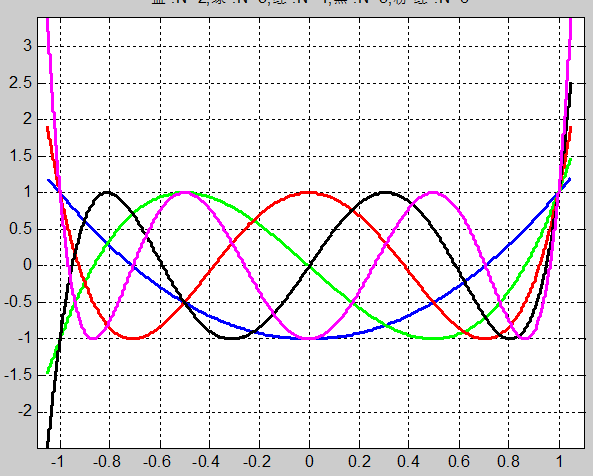
这样,我们就可以利用它的等波纹特点,构造滤波器的通带或阻带,而利用它的单调特性,构造过渡带。从而有两种类型的切比雪夫滤波器:

上面公式中,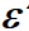 的取值范围为 0~1,表示波纹大小,其值越大,波纹越大;Wc为截止频率;CN为切比雪夫多项式,N为阶数。
的取值范围为 0~1,表示波纹大小,其值越大,波纹越大;Wc为截止频率;CN为切比雪夫多项式,N为阶数。
这两种滤波器的幅度特性分别如下图所示:
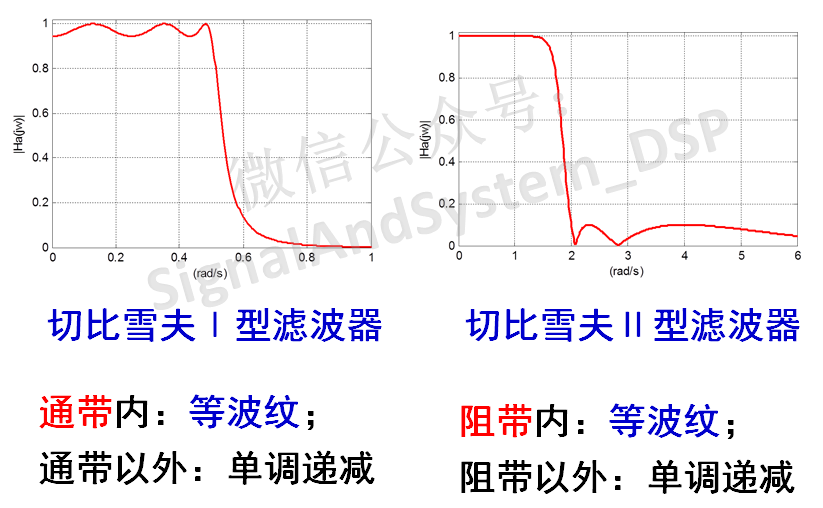
切比雪夫滤波器的设计方法,与巴特沃斯滤波器类似,也是根据滤波器技术指标,计算出N和Wc,查表得到归一化原型滤波器的系数,再去归一化,得到所需滤波器的系统函数系数。只是其计算过程更为繁琐。这里不再赘述。
四 椭圆滤波器
上面所说的两种类型的切比雪夫滤波器,分别实现了通带或者阻带内等波纹,而采用雅可比椭圆函数构造幅度平方函数的椭圆滤波器,在通带和阻带内都具有等波纹的特性。
下图为椭圆滤波器的幅度函数曲线。因为1931年考尔(Cauer)首先对这种滤波器进行了理论证明,故又称为考尔滤波器。
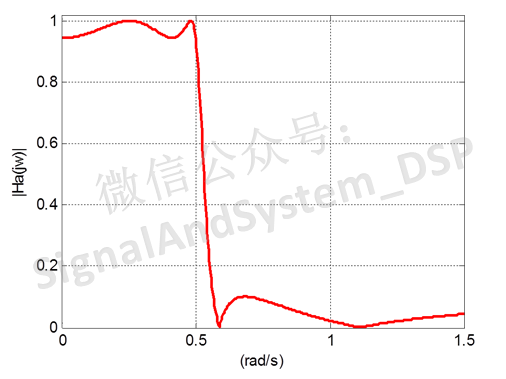
因其表达式较为复杂,此处不再赘述。
五 几种模拟滤波器的比较
上面介绍了几种常用的模拟滤波器,下面表格对这几种滤波器的幅度特性做了比较。
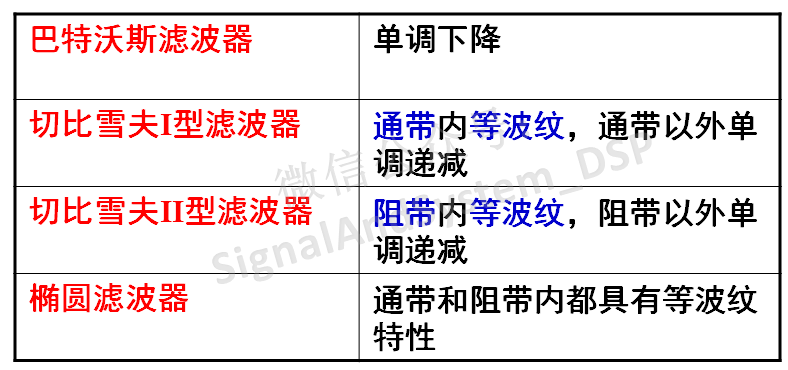
在满足相同的滤波器幅频响应指标条件下,巴特沃斯滤波器阶数最高,而椭圆滤波器阶数最低。
matlab中的信号处理工具箱中,提供了丰富的滤波器设计的函数。下表中给出了与本文这几种滤波器有关的函数。
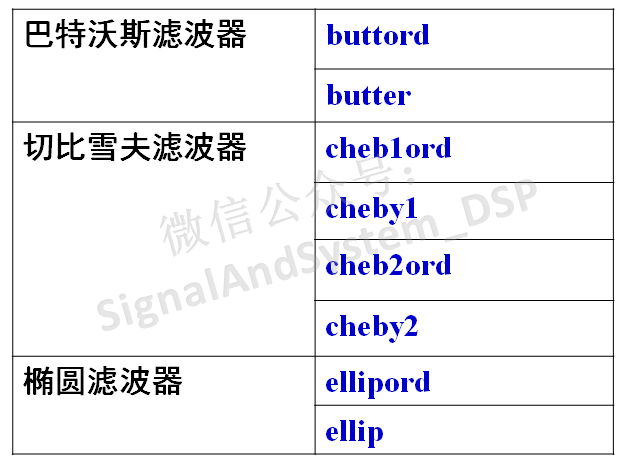
具体函数的使用方法,这里不再赘述,可以在matlab的帮助中查看。
本文的最后,结合一道例题,给出其matlab程序和仿真结果。

matlab仿真程序如下:
% 设计巴特沃斯模拟滤波器
%滤波器指标:通带截止频率:2000πrad/s,阻带截止频率:4000πrad/s,
%通带最大衰减:1dB,阻带最小衰减:40dB
%编写者:丹梅
close all;clear;clc;
%滤波器的性能指标
wp = 10002pi;%通带截止频率,单位:rad/s
ws = 20002pi;%阻带截止频率,单位:rad/s
Rp = 1;%通带最大衰减,单位:dB
Rs = 40;%阻带最小衰减,单位:dB
%----------------巴特沃斯滤波器--------------------%
% 计算满足性能指标的滤波器阶数n和3dB截止频率wn
[n_BW,wn_BW] = buttord(wp,ws,Rp,Rs,'s');
% 计算模拟低通滤波器的传输函数Ha(s)(传输函数为分子、分母多项式形式)
[b_BW,a_BW] = butter(n_BW,wn_BW,'s');
%----------------切比雪夫1型滤波器--------------------%
% 计算满足性能指标的滤波器阶数n和3dB截止频率wn
[n_CB1,wn_CB1] = cheb1ord(wp,ws,Rp,Rs,'s');
%注意:与buttord函数不同,cheb1ord函数返回参数的第二个wn就是wp,而不是3dB截止频率
% 计算模拟低通滤波器的传输函数Ha(s)(传输函数为分子、分母多项式形式)
[b_CB1,a_CB1] = cheby1(n_CB1,Rp,wn_CB1,'s');
%----------------切比雪夫2型滤波器--------------------%
% 计算满足性能指标的滤波器阶数n和3dB截止频率wn
[n_CB2,wn_CB2] = cheb2ord(wp,ws,Rp,Rs,'s');
%注意:与buttord函数不同,cheb1ord函数返回参数的第二个wn就是wp,而不是3dB截止频率
% 计算模拟低通滤波器的传输函数Ha(s)(传输函数为分子、分母多项式形式)
[b_CB2,a_CB2] = cheby2(n_CB2,Rs,wn_CB2,'s');
%----------------椭圆(考尔)滤波器--------------------%
% 计算满足性能指标的滤波器阶数n和3dB截止频率wn
[n_EL,wn_EL]=ellipord(wp,ws,Rp,Rs,'s');
% 计算模拟低通滤波器的传输函数Ha(s)(传输函数为分子、分母多项式形式)
[b_EL,a_EL]=ellip(n_EL,Rp,Rs,wn_EL,'s');
%---------------输出四种滤波器阶数-------------------%
display('巴特沃斯滤波器阶数:');n_BW
display('切比雪夫1型滤波器阶数:');n_CB1
display('切比雪夫2型滤波器阶数:');n_CB2
display('椭圆滤波器阶数:');n_EL
%---------------输出滤波器频率响应-------------------%
% 求模拟滤波器的频率响应(分析频率范围为w = 0~2*ws)
w = [0:1:500]2ws/500;
H_BW = freqs(b_BW,a_BW,w);
db_BW = 20*log10((abs(H_BW)+eps)/max(abs(H_BW)));
H_CB1 = freqs(b_CB1,a_CB1,w);
db_CB1 = 20*log10((abs(H_CB1)+eps)/max(abs(H_CB1)));
H_CB2 = freqs(b_CB2,a_CB2,w);
db_CB2 = 20*log10((abs(H_CB2)+eps)/max(abs(H_CB2)));
H_EL = freqs(b_EL,a_EL,w);
db_EL = 20*log10((abs(H_EL)+eps)/max(abs(H_EL)));
% 绘图(为了读数方便,横坐标对pi进行了归一化)
figure;
subplot(221);plot(w/pi,db_BW,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('巴特沃斯滤波器');grid on;
subplot(222);plot(w/pi,db_CB1,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('切比雪夫1型滤波器');grid on;
subplot(223);plot(w/pi,db_CB2,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('切比雪夫2型滤波器');grid on;
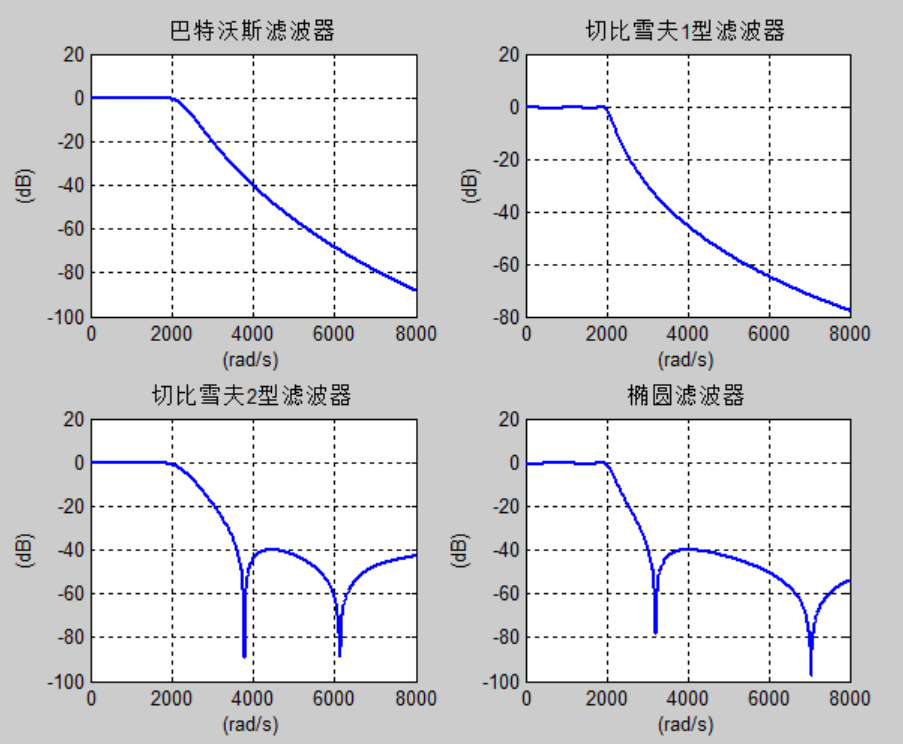
subplot(224);plot(w/pi,db_EL,'LineWidth',2);
xlabel('(rad/s)');ylabel('(dB)');title('椭圆滤波器');grid on;
运行结果如下:

-
模拟低通滤波器的设计方法有哪些2024-11-26 2253
-
巴特沃斯滤波器是模拟滤波器吗2024-05-22 2065
-
一种八腔带通腔体滤波器的设计方法2023-12-16 3277
-
fir滤波器设计方法有哪些2023-02-15 2472
-
求大佬分享一种有源滤波器合成方法2021-06-07 1228
-
模拟滤波器的设计方法2020-11-10 10389
-
一种基于经优化算法优化过的神经网络设计FIR滤波器的方法介绍2019-07-08 1304
-
一种新型SIW腔体双膜滤波器的设计方法介绍2019-07-03 2172
-
一种简单的介质波导双模滤波器设计方法介绍2019-06-25 1952
-
一种新颖的并联有源电力滤波器死区补偿方法_刘威葳2016-12-30 985
-
一种设计IIR QMF滤波器组的新方法2010-01-18 967
-
一种基于CMOS工艺射频有源滤波器的设计2009-12-14 947
-
模拟滤波器的应用2009-12-07 1637
-
一种消除有源电力滤波器系统振荡的控制方法2009-07-14 1009
全部0条评论

快来发表一下你的评论吧 !

