载波泄露和本振相噪对信号EVM的影响

载波泄露，大概的意思是，在信号上不应该有本振信号的，但是你却有了，是不小心泄露出来的。

当然泄露的路径多种多样，可能是基带信号的直流偏移(DC offset)，也可能是调制器端口之间的隔离度有限，也有可能是空间的某条耦合路径~

那么，载波泄露会对EVM产生什么影响呢？

为了说明这个问题，先看一下基带信号的直流偏移为啥会产生载波泄露。

假设基带信号为：

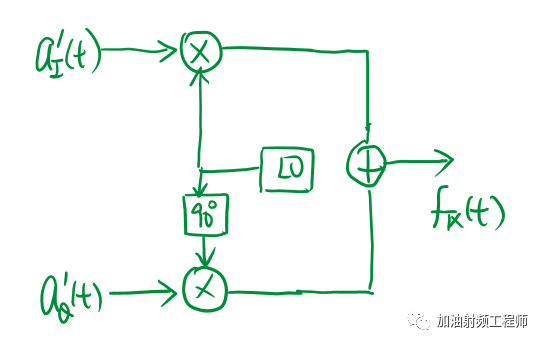
则经过上图所示的正交调制器以后，得到如下的信号：

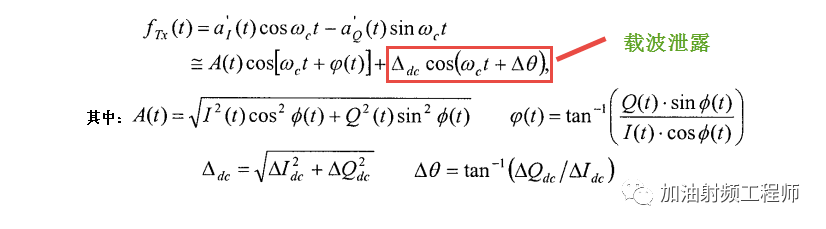
式子右边的红框框里，就是载波泄露，也称为载波馈通(CFT,carrier feed through).

上面这个式子呢，第一步，显而易见，按照上图的正交调制器的框图，划拉一下，就是这个等式。

但是，第二步是怎么来的？

dang~

推算步骤见下面。

不想看推导的，略过也行。

现在回到开头提到的那个问题，载波泄露会对EVM产生什么影响呢？

如果I路和Q路的基带信号有直流偏移，则在星座图上会发生星座图平移，如下图所示。

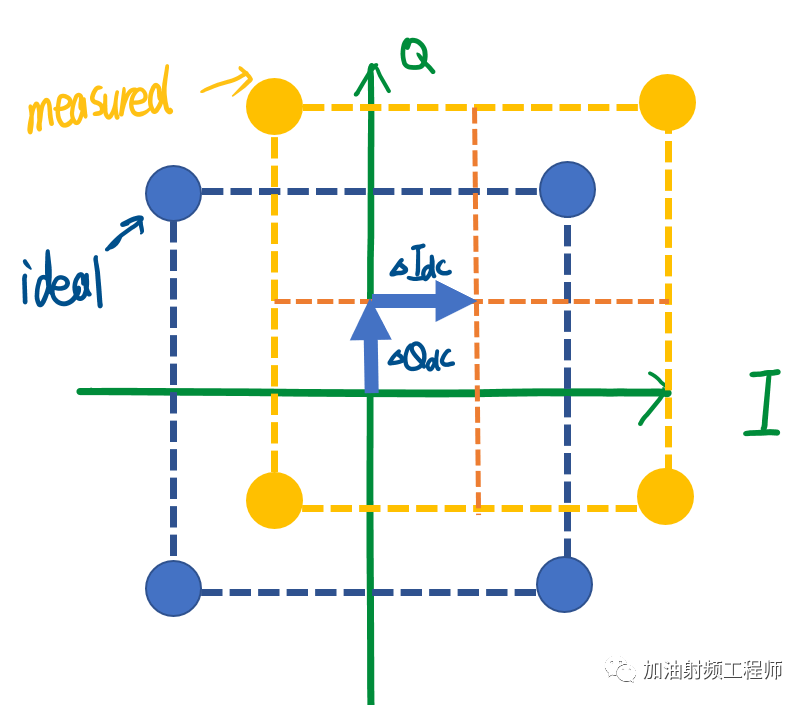
那这个带有直流偏移的I路和Q路基带信号，经过理想调制，给到理想的解调器，解调出的星座图，没有悬念的，肯定也是上面这幅图。

而，带有直流偏移的I路和Q路基带信号，经过理想调制器后，会产生载波泄露。

所以，可以认为，载波泄露会使得星座图发生平移。

也许，会有这样一个疑问哈！

那就是，你是直流偏移的I路和Q路基带信号，经过调制后，产生的载波泄露，会产生星座图平移。

那如果是别的途径来的载波泄露，是不是也会？虽然我觉得也会，因为可以对公式倒推，这样的话，从别的地方过来的载波泄露，也可以等价为基带信号上的直流偏移。但是用ADS仿真看了一下，发现平移没看到，反而旋转了。大家再讨论讨论。

那么，怎么量化本振泄露对EVM的影响呢？

定义载波抑制Cs为载波泄露功率与信号传输功率的比值，如下图所示。

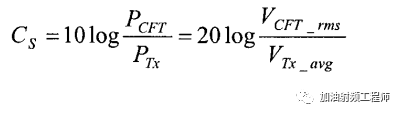
其中，PCFT为载波泄露的功率，PTX为有用信号的功率。

而由于载波泄露导致的EVM恶化，可由下式进行计算【1】：

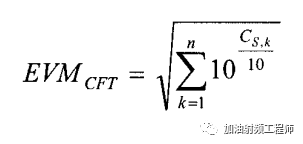
本来想用仿真来验证一下理论的。但是没成功，不知道是软件问题，还是我的问题。

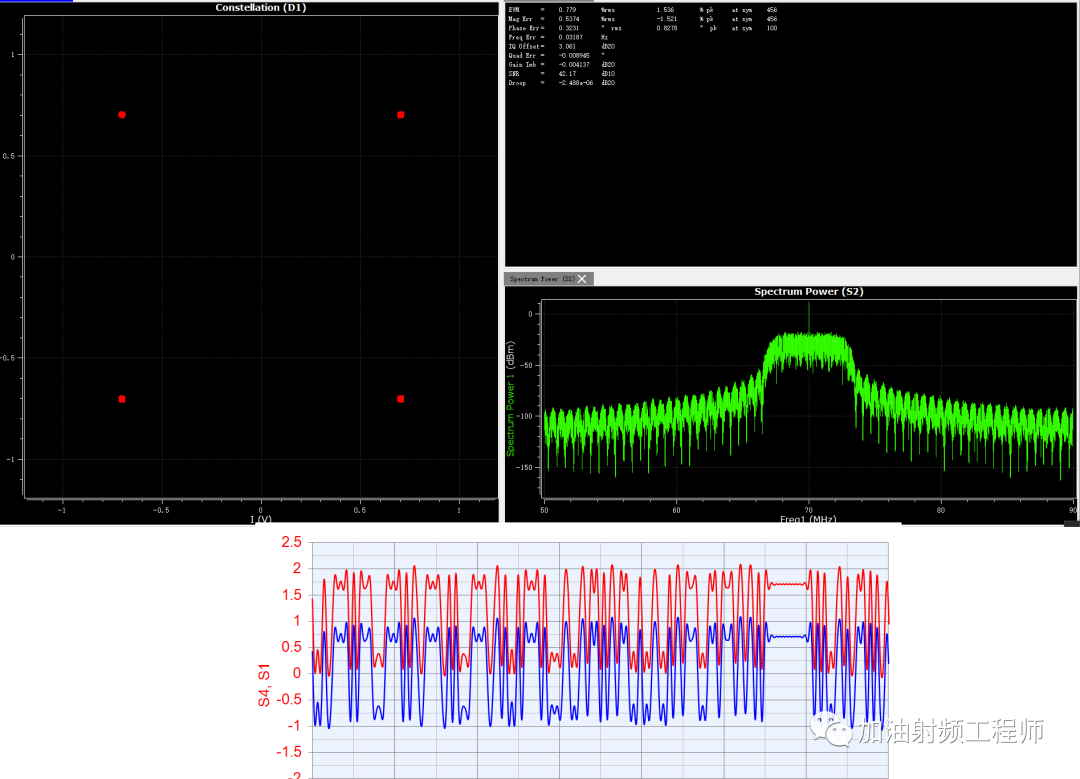
试了一下SystemVue，软件并没有给出想要的结果。星座图没有变化，EVM也没有变化，但是从频谱上看，确实是有一个很大的载波泄露，看基带信号，确实也有直流叠加上去了，而且幅度还不小，不能忍！

没办法，我又折回ADS，用以前仿接收机的那一套，试了一下，发现比SystemVue好一点，能看到本振泄露，也能看到星座图上确实是有了偏移，这到是和理论能对上。但是EVM反而变小了，不能忍！

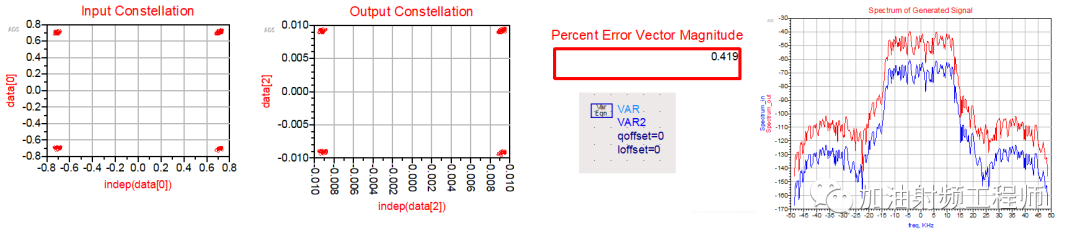
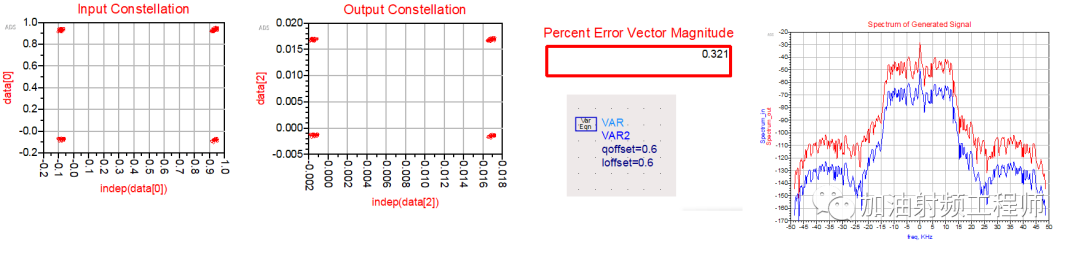
不知道matlab是个什么表现。本来很想试一下，奈何还完全不会！

参考文献：

[1] RF System Design of Transceivers for Wireless Communication.pdf

发射机中的本振相噪，是影响发射信号EVM的一个因素。

先来看看理论分析。

首先来看看EVM的定义。

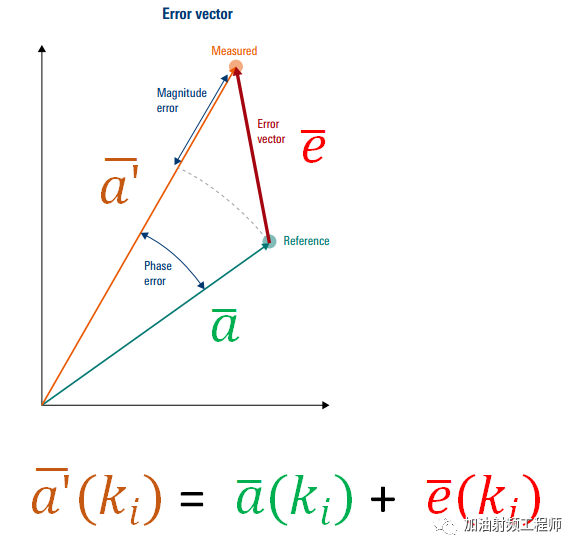
对于每一个符号而言，有一个理论上的位置，即上图中的绿点(Reference)，但是实际上，符号对应的点，在星座图上会有偏移，如上图中的桔黄色的点(Measured)。

而理想和现实之间的差距，即是误差矢量，如上图红色箭头所示。

由上图可知，对于每一个符号ki, 误差矢量可以由下式进行表示：

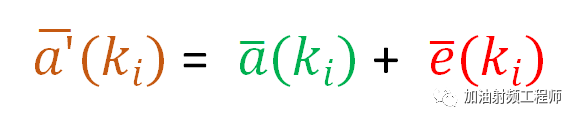
在文献[1]中，对EVM的定义是这样的：

我的理解是这样的，就是，虽然针对单个符号可以计算EVM，但是书中的定义，是基于多个符号对应误差矢量的平均值。

其数学表达式为：

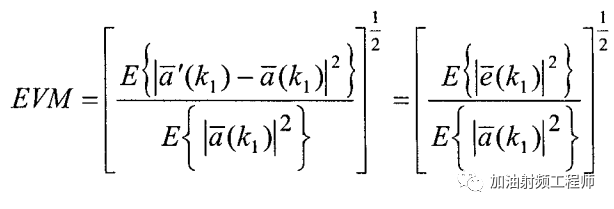
然后再看看怎么把相位噪声换算到EVM上。

既然，现在只是考虑相位噪声对EVM的影响，所以可以不考虑幅度误差。

并且，假设上述的矢量误差，是由于本振的相噪引起的。

本振的相噪，可以看成是一个很小的随机相位量，定义为：

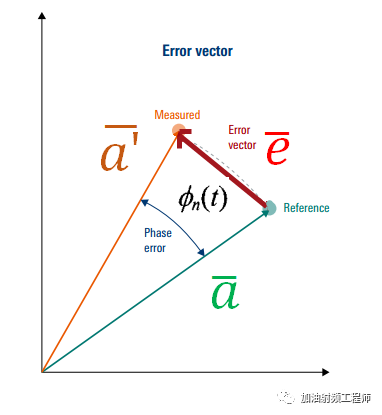
所以，实测的信号，可以用下式进行表示：

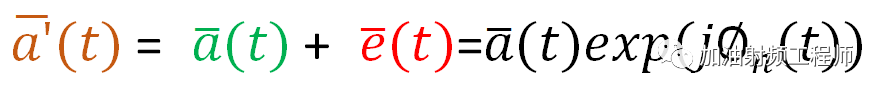
因此，误差矢量的幅度如下图所示：

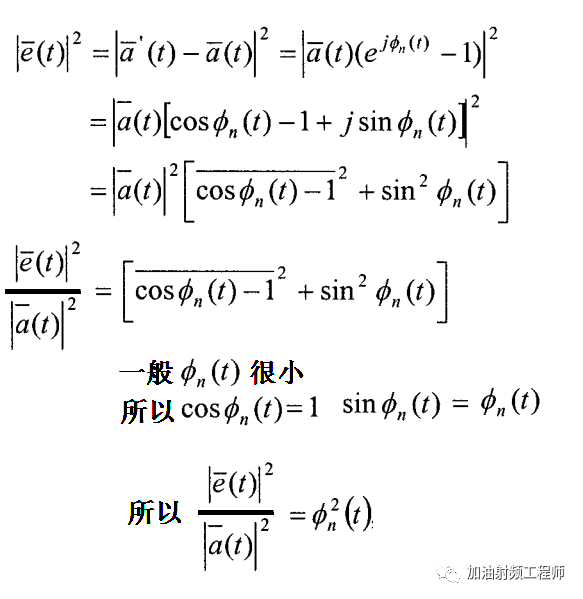
相噪的自相关函数与其对应的功率谱密度有如下的关系(我随机过程学的不好，所以下面的式子，并不是很理解，先copy过来)。

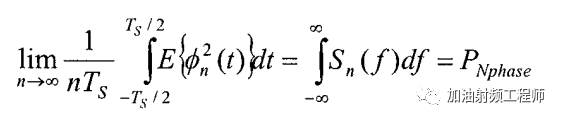
所以（在文献[1]的基础上，补了个dt，还有绿圈中为啥又不是Ts了呢？不过可以先看结论）:

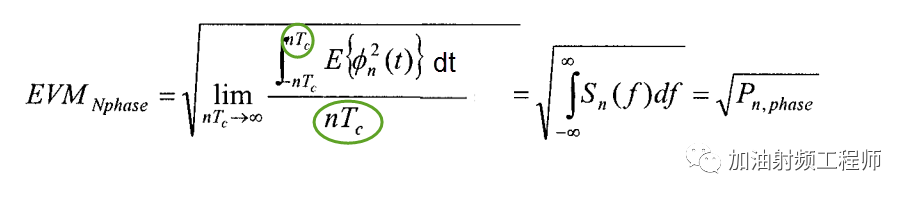
假设本振的环路带宽相对较宽，则由于相噪累积出来的能量为：

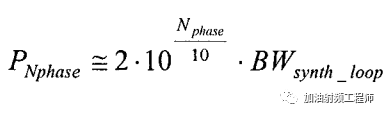
其中，Nphse是平均相噪，单位为dBc/Hz，BWsynth_loop是环路滤波器的带宽，单位为Hz。

所以，

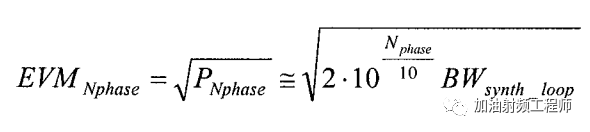
如果使用了多个本振，则

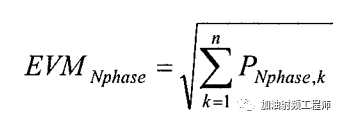
然后再看看仿真验证。

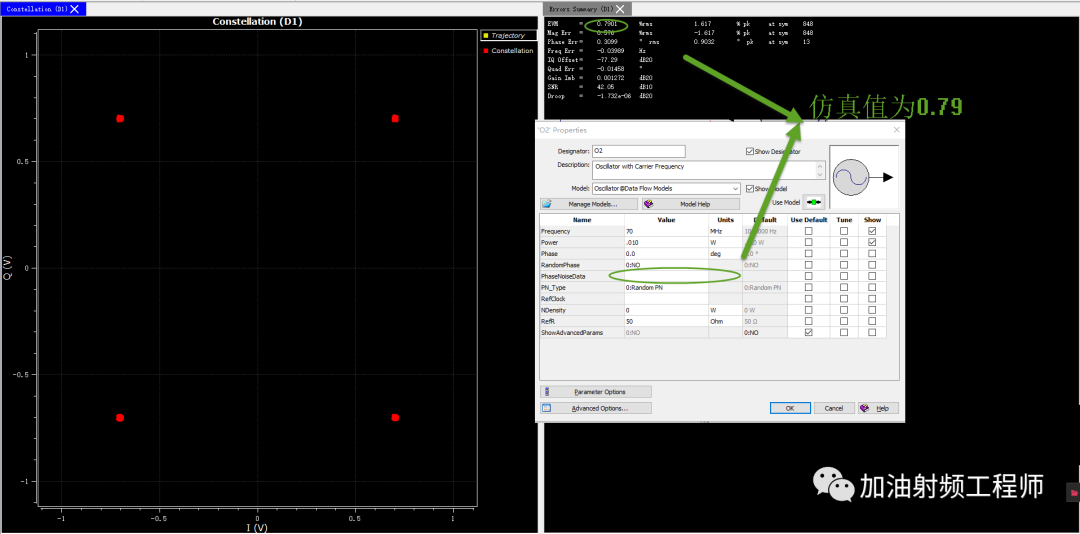
用SystemVue进行验证，发现当LO不考虑相噪时，EVM为0.79%。

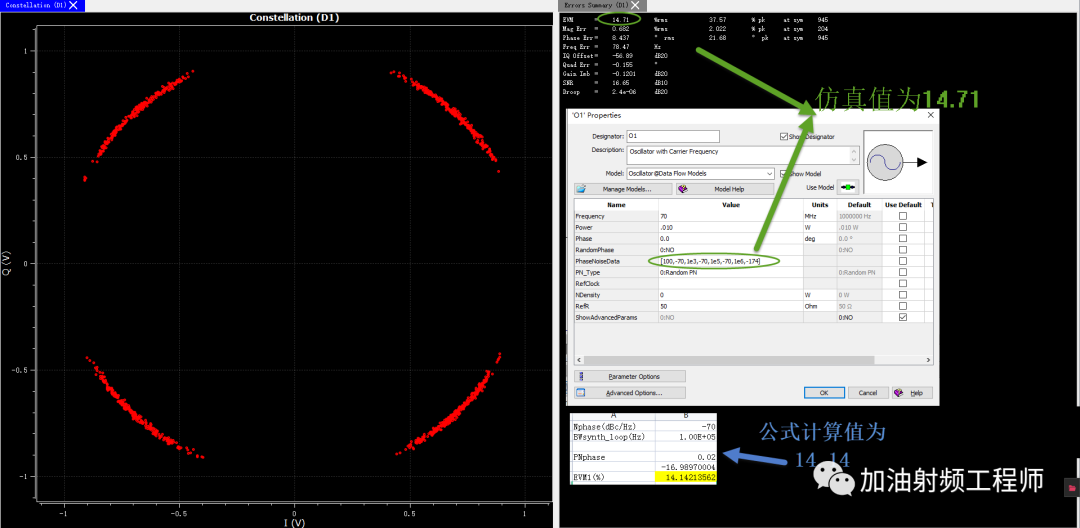
当相噪为:

-70dBc/Hz@100Hz,

-70dBc/Hz@1000Hz

-70dBc/Hz@100KHz

-174dBc/Hz@1MHz

时，仿真得到的值为14.71%，而根据上述公式，计算得到的值为14.14%。两种结果对比来看，理论公式的预估还是比较准确的。

同时，可以从星座图中看到，测量点成为一个弧形，这也与开头的假设相呼应，即没有幅度误差或者很小，只有相位误差。

审核编辑：汤梓红