

关于FFT的信号补零操作
电子说
1.4w人已加入
描述
在做信号处理的过程中,常遇到将信号补零后再做FFT等操作,比如频域脉冲压缩算法中,一般距离维PRT数据和脉压系数需要填零使长度相等且满足2的N次方,但是填零操作能做什么,不能做什么呢?
先说结论:补零不会改变频谱的样子(轮廓),也就是不会改变频率分辨率,但会减弱栅栏效应,提高频谱分辨率,也就是频谱采样点会增加,导致频谱采样间隔减小。注意,频谱分辨率和频率分辨率的区别。
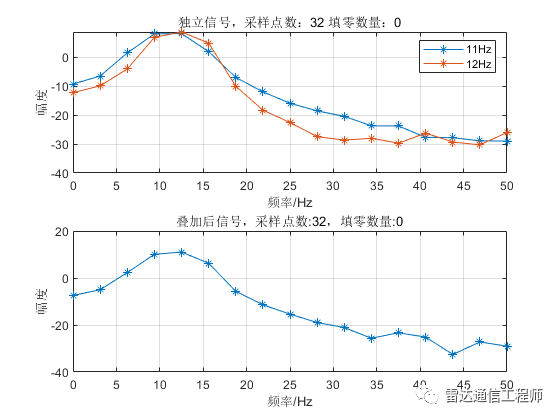
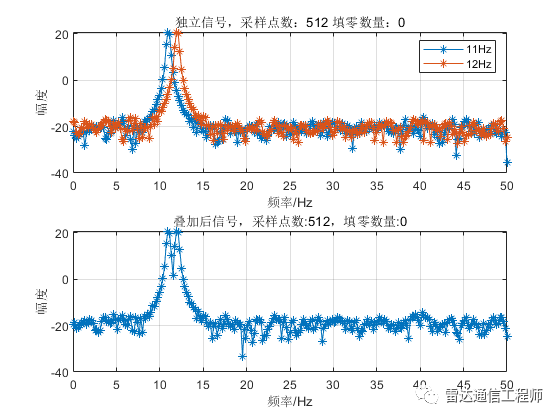
示例中使用100Hz采样率产生两个单频点正弦信号,频率分别为11、12Hz;接着两者分别做FFT运算,以及两信号叠加后做FFT;
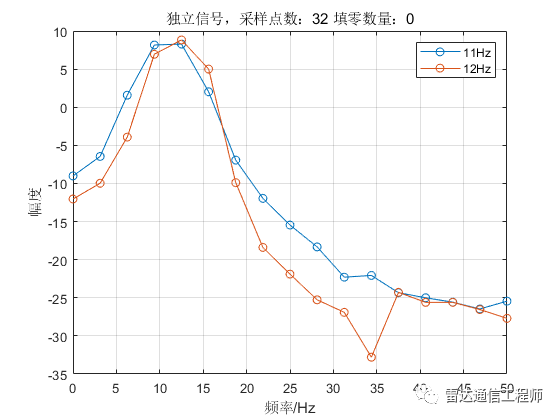
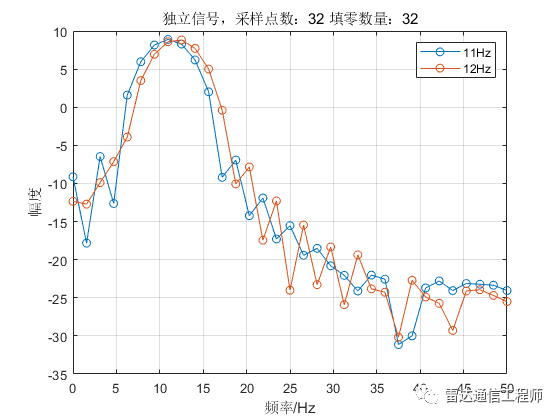
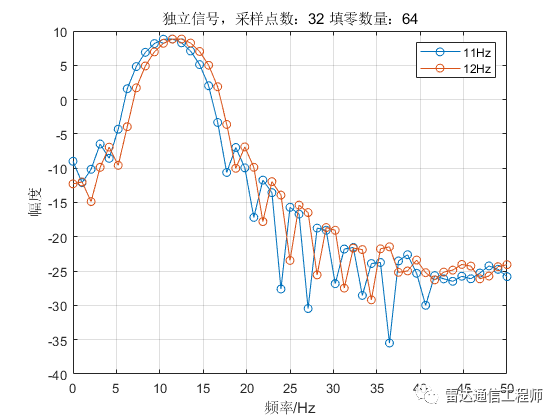
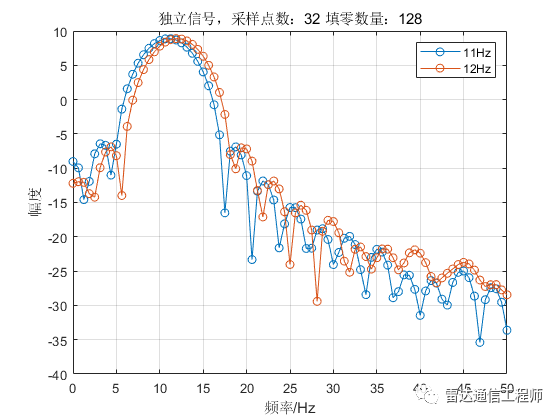
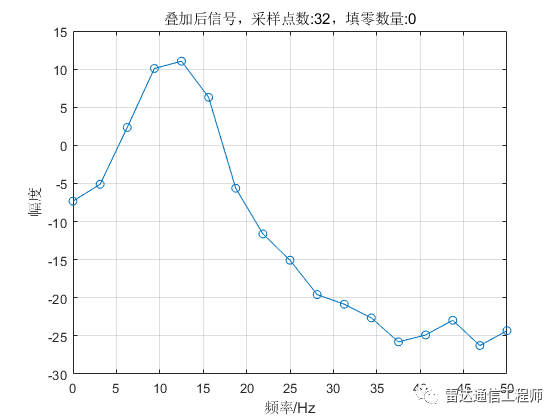
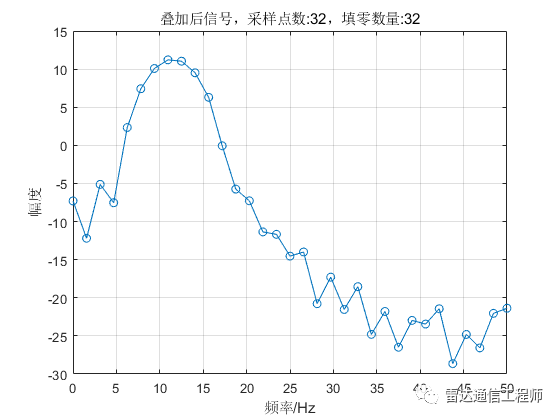
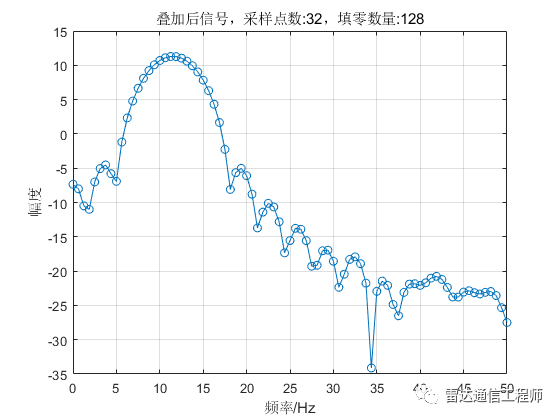
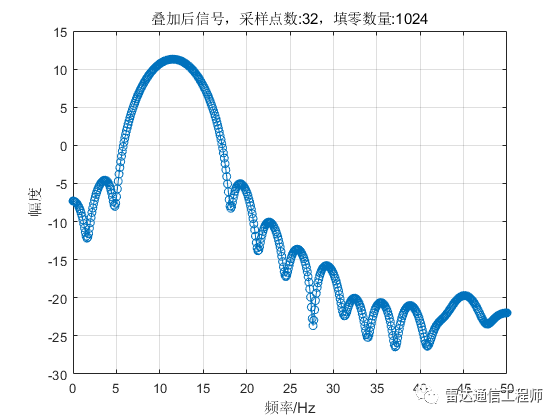
从以上各图可以看出,随着填零数量的增加,频谱的基本轮廓并未改变,只是变得更细腻(提高了频率颗粒度,即频谱分辨率),但是并不能提高频率分辨率,从图形上直观体现为主瓣尖峰宽度不变,图中11Hz和12Hz的正弦信号频谱峰值难以分辨;
从原理上分析,采样率100Hz,N=32点,则FFT频率分辨率fs/N=3.125Hz,则本例中1Hz的差异是无法分辨的,不断的填充0相当于在频域进行插值,随着填零数量的增加,32点的FFT信号频谱将不断逼近离散时间傅里叶变换(DTFT)的结果;反过来理解(将图按从下往上的顺序看),在N=32不变的情况下,填零后FFT相当于在32点信号DTFT结果中一个频域周期内进行等间隔采样而来。
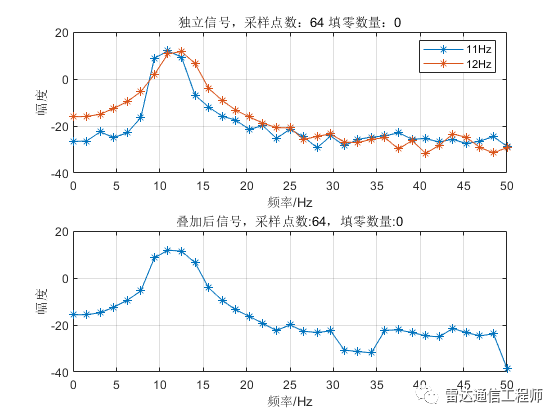
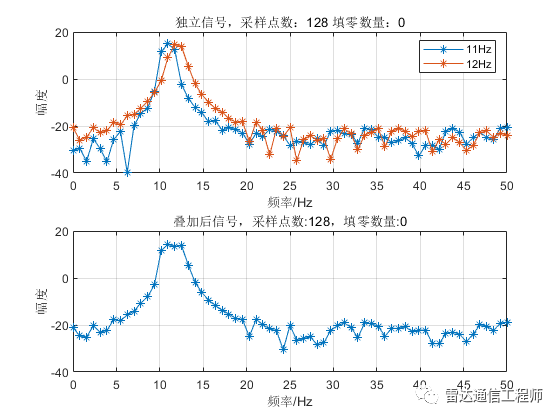
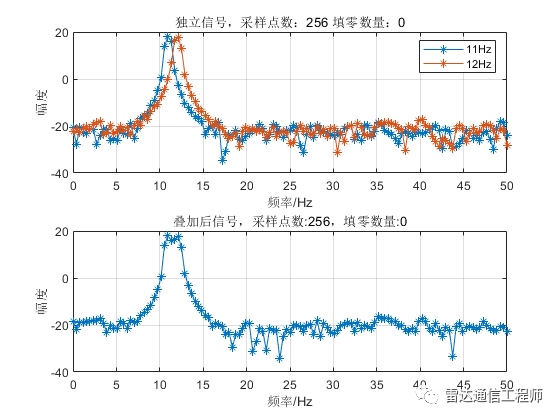
提高频率分辨率需要增加观测时间(即有效数据长度),如需要分辨1Hz的频率,就需要至少1/1Hz=1s的有效观测时长;下面看看增加采样点数后频谱的变化,图中分别有11、12Hz两个频率的独立频谱和时域叠加后的频谱,可以看到在N大于128点开始,叠加信号主瓣上开始出现两个非相邻独立峰值点,N越大,区分越明显。单频信号的主瓣宽度随着N增加而变窄。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
STM32的DSP库函数FFTarm_fft_bin_example里面,为什么.arm_fft_bin_data.c的数据都是隔一个位置补0的?2024-05-08 443
-
信号补零对信号频谱的影响是什么2025-11-21 53
-
Matlab关于FFT算法的编程及原理详细讲解2010-11-14 111610
-
BLE一次广播的字节数一定是32个吗,剩余自动补零?2016-04-07 4452
-
有关fft做相关运算问题,求大神帮帮2017-12-23 3770
-
调用STM32的DSP库做fft运算补零是为了补充虚部吗?2019-02-22 3704
-
FFT返回的峰值频率总是零2019-09-18 3803
-
为什么要用傅里叶变换?FFT你不知道的细节2023-06-20 2593
-
labview补零小功能2023-08-19 3758
-
理解FFT和信号加窗原理及意义2017-11-16 195084
-
基于FFT的正弦信号频率估计算法2017-12-29 1593
-
数字信号处理 FFT分析信号频谱2019-05-07 15648
-
FFT帮你快速定位干扰信号来源2022-08-27 2936
-
信号基础:频域、时域、FFT和加窗2023-04-11 5598
-
傅里叶变换补零到底有什么用,什么时候需要补零呢?2023-08-09 15883
全部0条评论

快来发表一下你的评论吧 !

