

FFT卷积是什么?FFT卷积基本过程描述
电子说
1.4w人已加入
描述
信号与系统基础之卷积定理:频域乘积相当于时域卷积,千万不要问我什么,可以去看看教材上的公式推导。
运算效率对比分析,使用FFT快速卷积法(实线)明显比时域卷积乘法次数要少,一般而言64点以上,FFT法就具有优势。
FFT卷积基本过程描述:设信号x长度n,卷积系数h长度为k,则时域卷积结果长度为L=n+k-1,为了采用高效的基2型FFT算法,需要将信号和系数均在末尾补零扩展到最接近的2的N次方长度m(比如n=32,k=16,则L=32+16-1=47,最近的2的N次方为64),然后分别做m点FFT变换到频域后再复乘,最后IFFT变回时域。
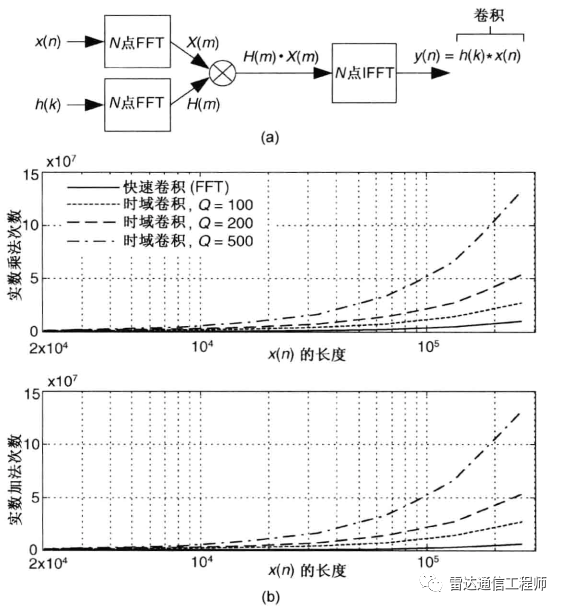
从上理论就讲说这么多,更详细的可看看相关专著书籍,接下来用matlab仿真来看看运算过程的中间环节是什么样;
clc;
clear;
%%设定信号参数
T=10e-6; %信号长度:us
f0=3e6; %信号1:3MHz
f1=8e6; %信号2:8MHz
fs=80e6; %信号采样率:MHz
t=-T/2:1/fs:T/2-1/fs; %时间序列
%加载fdatool设计的滤波器FIR系数
load("coef.mat");
%滤波器频率响应
freqz(coef,1,200,fs);
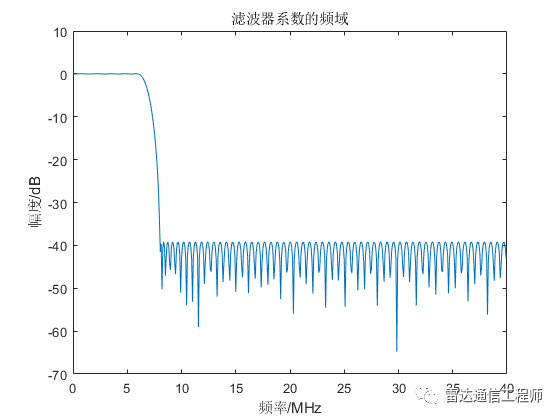
%低通滤波器参数:3MHz带宽,截止频率4MHz,带外抑制80dbc
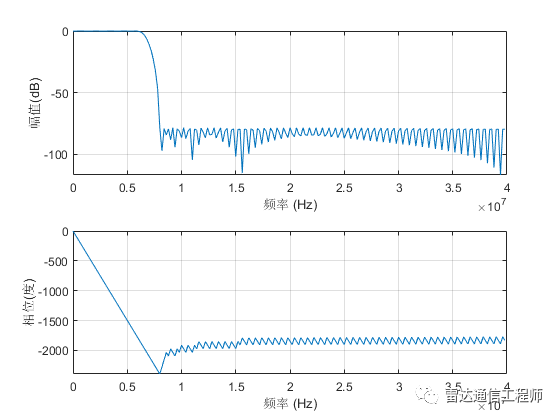
信号和变量长度

信号长度800,系数长度134,则卷积结果长度为800+134-1=933,因此需要补零扩展到1024点;
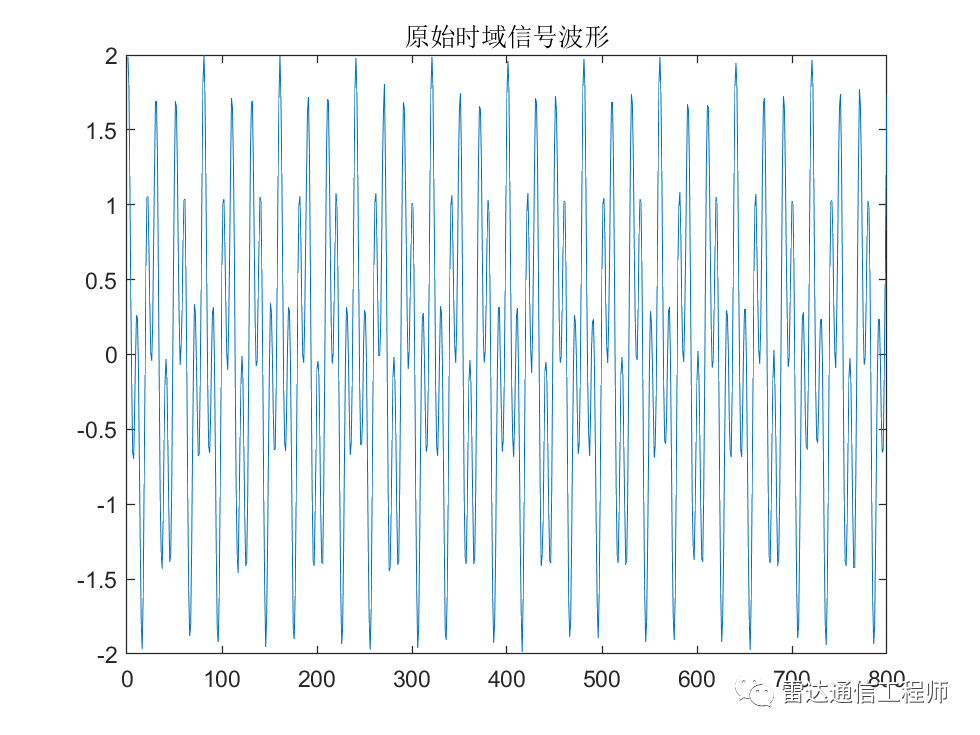
%生成信号:模拟采样过程
if_sig=cos(2*pi*f0*t)+cos(2*pi*f1*t);
%加入白噪声SNR=30dB
if_sig=awgn(if_sig,30,'measured');
% if_sig=round(8192*if_sig); %中频信号
plot(if_sig);title('原始信号');
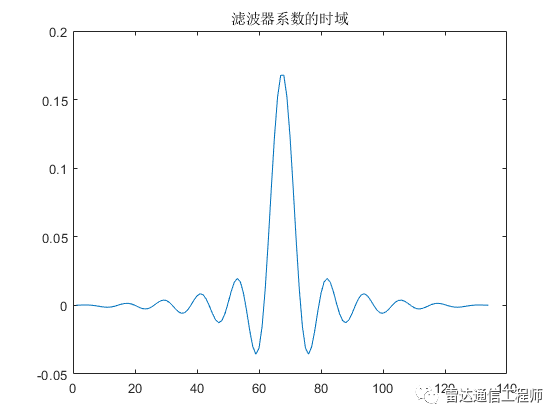
plot(coef);title('滤波器系数的时域');
coef_fft = fft(coef,1024);
len=length(coef_fft);
f_x=(0:len-1)*fs/len;%频率序列
f_x=f_x/1e6;
plot(f_x(1:len/2+1),10*log10(abs(coef_fft(1:len/2+1))));
title('滤波器系数的频域');
xlabel('频率/MHz');ylabel('幅度/dB');
此处留一个坑,下回继续
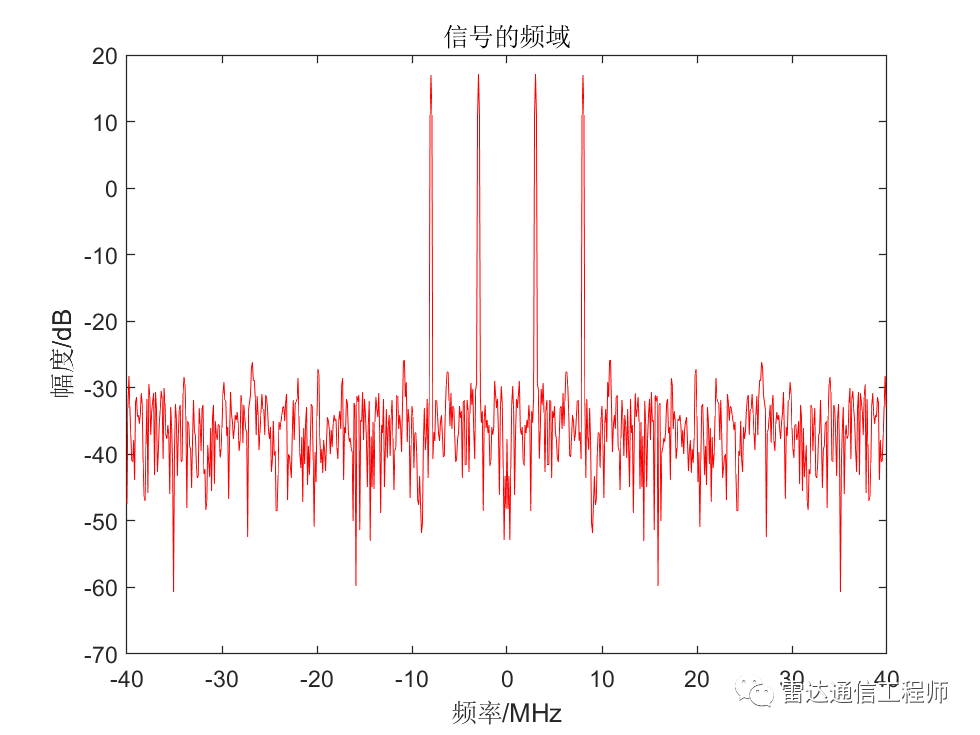
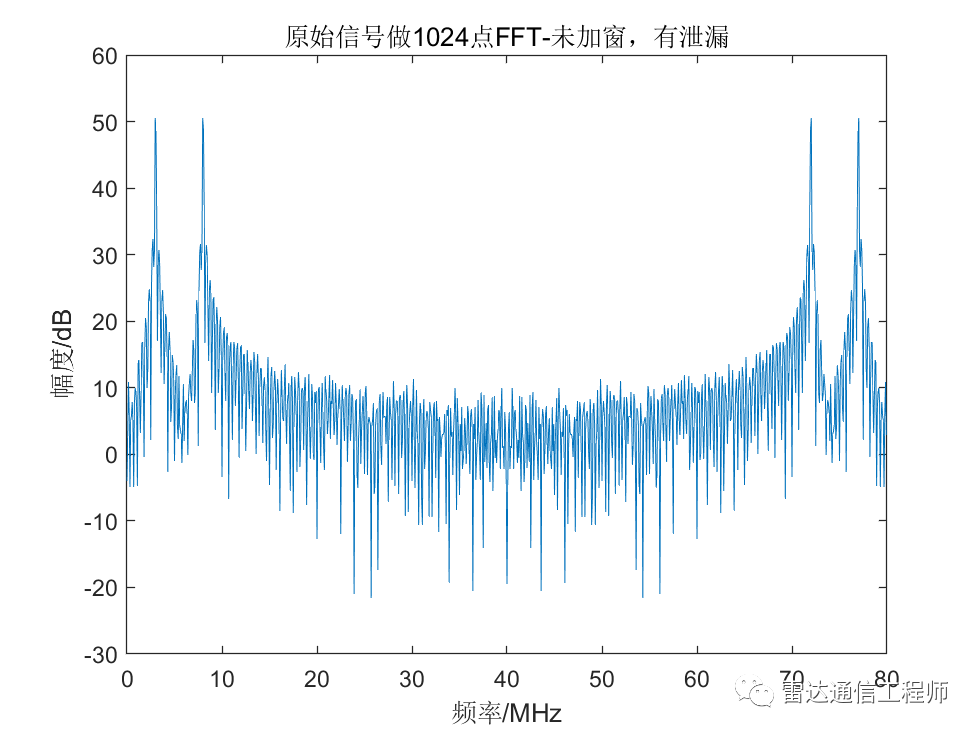
sig_fft = fft(if_sig,1024);
plot(f_x,20*log10(abs(sig_fft)));
title('原始信号做1024点FFT');
xlabel('频率/MHz');ylabel('幅度/dB');
%频域相乘,注意此处为复数乘法
conv_fft = sig_fft.*coef_fft;
plot(f_x,20*log10(abs(conv_fft)));
title('信号和系数频域乘积后');
xlabel('频率/MHz');ylabel('幅度/dB');
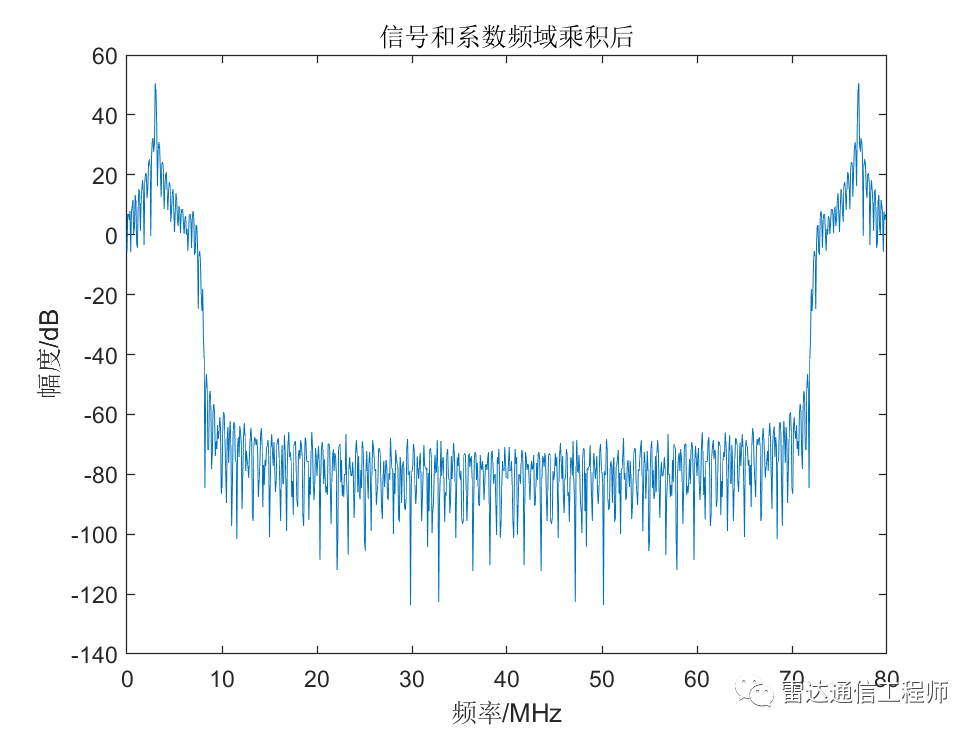
上图为频域滤波后结果,可以看到8MHz的带外信号被滤除,剩下3MHz的带内信号;接下来就是变换回时域波形。
%IFFT变换还原到时域
fft_filter_out = ifft(conv_fft);
plot(fft_filter_out);
title('FFT卷积频域滤波后的信号波形');
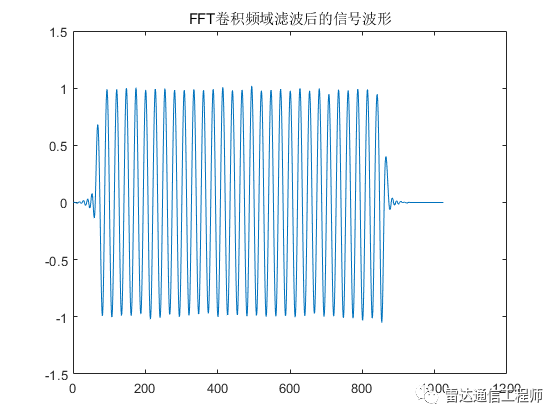
为了方便对比,下边给出通过时域卷积方式的运算结果
%时域卷积方式滤波
conv_filter_out = conv(if_sig,coef);
plot(conv_filter_out);xlim([1,1200]);
title('时域卷积方式滤波后的信号波形');
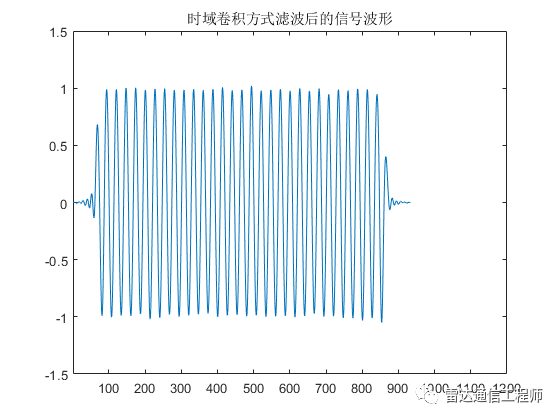
从上面时域处理、频域处理的结果可以看到,两者处理后时域处理的结果和频域处理后的前933个点的结果相同。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
卷积运算分析2025-10-28 100
-
什么是卷积码? 什么是卷积码的约束长度?2008-05-30 20046
-
FFT与DFT计算时间的比较及圆周卷积代替线性卷积的有效性实2011-12-29 5191
-
卷积特性(卷积定理).ppt2017-10-03 4638
-
卷积特性(卷积定理).zip2017-10-04 2734
-
卷积神经网络一维卷积的处理过程2021-12-23 1790
-
简谈卷积—幽默笑话谈卷积2023-05-25 877
-
利用FFT IP Core实现FFT算法2008-01-16 7980
-
什么是卷积_卷积的意义2017-11-28 162533
-
卷积特性(卷积定理)2017-12-06 984
-
FFT三峰插值修正的电能计量新算法2018-03-10 868
-
一维卷积、二维卷积、三维卷积具体应用2018-05-08 5434
-
详解卷积神经网络卷积过程2019-05-02 19108
-
卷积神经网络的基本原理、结构及训练过程2024-07-02 4970
-
卷积神经网络计算过程和步骤2024-07-03 1957
全部0条评论

快来发表一下你的评论吧 !

